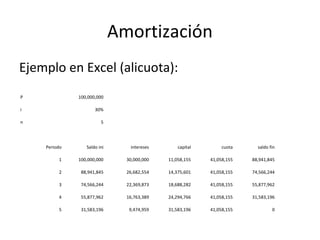
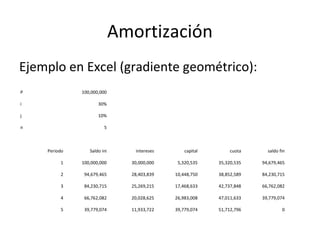
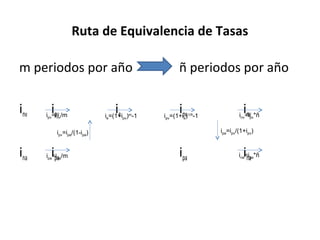
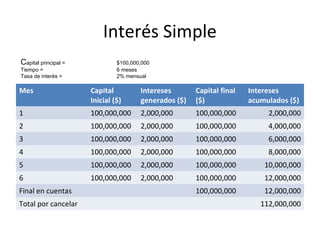
El documento trata sobre conceptos básicos de interés y tasas de interés. Explica que el interés es el rendimiento por el alquiler temporal del dinero y que la tasa de interés es la expresión porcentual del interés. También describe las modalidades de interés simple y compuesto, y presenta fórmulas para calcular valores presentes, futuros, tasas e intervalos de tiempo para escenarios de interés simple y compuesto.

1. MATEMÁTICAS FINANCIERAS

2. Interés y Tasas de Interés
Alvaro Hernán Sarria

3. Interés y Tasas de interés
Definición
El rendimiento que proporciona el enajenamiento temporal
del dinero, es decir, el importe del alquiler del dinero.
Como importe de alquiler que es, el interés debe referirse a
períodos de tiempo y según el capital comprometido.
La expresión porcentual del interés se denomina TASA DE
INTERES.

4. Modalidades de Interés
Cuando los intereses se acumulan dan lugar a dos
modalidades de acumulación:
• Interés Simple – los intereses se acumulan en una cuenta
aparte.
• Interés Compuesto – los intereses se acumulan en la misma
cuenta del capital, es decir, son objeto de generar más
intereses una vez capitalizados.
El interés compuesto capitaliza los intereses mientras que el
simple no lo hace.

5. Interés Simple
Mes Capital
Inicial ($)
Intereses
generados ($)
Capital final
($)
Intereses
acumulados ($)
1 100,000,000 2,000,000 100,000,000 2,000,000
2 100,000,000 2,000,000 100,000,000 4,000,000
3 100,000,000 2,000,000 100,000,000 6,000,000
4 100,000,000 2,000,000 100,000,000 8,000,000
5 100,000,000 2,000,000 100,000,000 10,000,000
6 100,000,000 2,000,000 100,000,000 12,000,000
Final en cuentas 100,000,000 12,000,000
Total por cancelar 112,000,000
Capital principal = $100,000,000
Tiempo = 6 meses
Tasa de interés = 2% mensual

6. Interés Compuesto
Mes Capital
Inicial ($)
Intereses
generados ($)
Capital final
($)
Intereses
acumulados ($)
1 100,000,000 2,000,000 102,000,000
2 102,000,000 2,040,000 104,040,000
3 104,040,000 2,080,800 106,120,800
4 106,120,800 2,122,416 108,243,216
5 108,243,216 2,164,864 110,408,080
6 110,408,080 2,208,162 112,616,242
Total por cancelar 112,616,242
Capital principal = $100,000,000
Tiempo = 6 meses
Tasa de interés = 2% mensual

7. Interés Simple - Fórmulas
Monto de Intereses
I = P * i * t
donde:
I: Monto de interés ($)
P: Monto de capital principal ($)
i: Tasa de interés por período (%)
t: Número de períodos (días, meses, años, etc.)

8. Ejemplo:
Calcular el monto de interés que paga un préstamo de
$500,000 al 1.5% mensual por 18 meses:
Capital: $500,000
Tasa de interés: 1.5% = 0.015
Tiempo: 18 meses
I = $500,000 * 0.015 * 18 = $135,000
Interés Simple - Fórmulas

9. Relación entre valor presente y valor futuro
VF = P + I
VF = P + P*i*t = P (1 + i * t)
Ejemplo:
Calcular el valor a pagar en 18 meses cuando se cumpla un
préstamo por $500,000 al 1.5% mensual simple.
I = $500,000 * 0.015 * 18 = $135,000
VF = $500,000 + $135,000 = $635,000 o
VF = $500,000 * (1 + 0.015 * 18) = $635,000
Interés Simple - Fórmulas

10. Relación entre valor presente y valor futuro
VP = F / (1 + i * t)
Ejemplo:
Calcular el valor presente de una deuda que debe cancelar
$3,000,000 dentro de 18 meses si el interés pactado es del 3%
mensual:
VP = $3,000,000 / (1 + 0.03 * 18) = $1,948,052
Interés Simple - Fórmulas

11. Cálculo de Tasa de Interés
i = (VF/P -1)/t
Ejemplo:
Calcule la tasa de interés mensual que se aplica a un
préstamo de $1,948,052 que cancela $3,000,000 a los 18
meses:
i = ($3,000,000/ $1,948,052 – 1)/18 = 0.03 = 3% mensual
Interés Simple - Fórmulas

12. Cálculo de Tiempo
t = (VF/P -1)/i
Ejemplo:
Calcule el tiempo necesario para que una deuda de
$1,948,052 de convierta en $3,000,000 al 3% mensual:
t = ($3,000,000/ $1,948,052 – 1)/0.03 = 18 meses
Interés Simple - Fórmulas

13. Equivalencia de tasas:
Tasa nominal o anual (in) = ip*n
Donde n el número de períodos en un año.
Igualmente,
Tasa periódica (ip) = in/n
Interés Simple - Fórmulas

14. Relación entre valor presente y valor futuro
Interés Compuesto
Período Capital al inicio
del período
Interés del
período
Capital al final del período
1 P P*i P + P*i = P(1+i)
2 P(1+i) P(1+i)i P(1+i)+P(1+i)i=P(1+i)(1+i)=P(1+i)2
3 P(1+i)2
P(1+i)2
i P(1+i)2
+P(1+i)2
i=P(1+i)2
(1+i)=P(1+i)3
*
*
n P(1+i)n-1
P(1+i)n-1
i P(1+i)n-1
+P(1+i)n-1
i = P(1+i)n-1
(1+i) =
P(1+i)n
VFn = P(1+i)n

15. Ejemplo:
Un depósito de $5,000,000 se mantiene por cuatro
años en una fiducia que capitaliza intereses y ofrece
una tasa de interés del 1.5% mensual. ¿Cuánto se
retira al final de los cuatro años?
VF = $5,000,000*(1+0.015)4*12
VF = $10,217,391
Interés Compuesto

16. Similarmente:
VP = F / (1 + i)n
Ejemplo:
¿Cuánto debo invertir en la misma fiducia anterior si
quiero retirar $1,000,000 en 12 meses (i=1.5% mes)?
VP=$1,000,000/(1.015)12
=$836,387.42
Interés Compuesto

17. Similarmente, despejando para i
i = (F / P)1/n
– 1
Ejemplo:
¿Qué tasa de interés mensual triplica una inversión
en un año?
i = (3P / P)1/12
– 1 = 31/12
– 1 = 0.0959 = 9.59% mensual
Interés Compuesto

18. Finalmente despejando para n
n = log(F / P) / log(1 + i)
Ejemplo:
¿En cuanto tiempo se triplica una inversión al 3%
mensual?
n = log(3P/P) / log(1+0.03) = log(3)/log(1.03) = 37.17 meses
Interés Compuesto

19. Interés Compuesto
Flujos de Fondos Múltiples
Hasta ahora hemos trabajado solamente con un flujo
de fondos. En la vida real generalmente son flujos
múltiples:
FF0
0 1 2 3 4 n
FF1
FF2 FFn
FF3 FF4

20. Interés Compuesto
Flujos de Fondos Múltiples
Cálculo de valor presente:
VP
0 1 2 3 4 n
FF1
FF2 FFn
FF3 FF4

21. Interés Compuesto
Flujos de Fondos Múltiples
Cálculo de valor futuro:
0 1 2 3 4 n
FF1
FF2 VF
FF3 FF4

22. Ejemplo Flujos Múltiples:
Un padre requiere pagar las cuotas universitarias de sus hijos
en Enero, Marzo y Abril (último día del mes) por valor de $5,
$7 y $12 millones respectivamente. El 31 de Diciembre recibe
la prima y quiere saber cuanto debe ahorrar de ella para
poder cubrir las cuotas si su inversión renta 2.5% mensual?
Interés Compuesto
VP
0 1 2 3 4 12
5
7
12
431
)025.1(
12
)025.1(
7
)025.1(
5
++=VP
VP = $22.25 MM

23. Ejemplo Flujos Múltiples:
Un pobre empleado puede ahorrar $30, $40, $50 y $50
millones en uno, dos, tres, cuatro meses respectivamente
para un viaje al exterior que tiene planeado dentro de un
año. Si la inversión le da el 3% mensual, cuánto tendrá para su
viaje?
Interés Compuesto
412312212112
%)31(*50%)31(*50%)31(*40%)31(*30 −−−−
+++++++=VF
VF
0 1 2 3 4 12
30 40
50 50
VF = $223.86 MM

24. Como caso especial de lo anterior que pasa cuando los flujos
son todos iguales:
Interés Compuesto
VP
0 1 2 3 … n-1 n
A A A A A A

25. Interés Compuesto






+
−+
=






+
−+
=⇒





+
−+
=−+








+
−+
=





+
−
+
+
=





+
−=−+=−






+
+
+
++
+
+
+
+=+






+
+
+
++
+
+
+
+
+
+=+






+
+
+
++
+
+
+
+
+
=
+
+
+
++
+
+
+
+
+
=
−−
−
−
−
n
n
n
n
n
n
nnn
n
n
nn
nn
nn
nn
ii
i
AVP
i
i
AVPi
i
i
AiVP
i
i
A
ii
i
A
i
AVPiVPecec
ec
iiii
AiVP
iiiii
AiiVP
ec
iiiii
AVP
i
A
i
A
i
A
i
A
i
A
VP
n
)1(
1)1(
)1(
1)1(
)1(
1)1(
)11(
)1(
1)1(
)1(
1
)1(
)1(
)1(
1
1)1(12
2
)1(
1
)1(
1
...
)1(
1
)1(
1
1)1(
)1(
1
)1(
1
...
)1(
1
)1(
1
)1(
1
)1()1(
1
)1(
1
)1(
1
...
)1(
1
)1(
1
)1(
1
)1()1(
...
)1()1()1(
1221
1321
1321
1321

26. Despejando de la ecuación anterior podemos
encontrar la formula para A (alicuota)
para futuros, como VFn=P(1+i)n
Interés Compuesto
1)1(
)1(
−+
+
= n
n
i
ii
PVA
i
i
Ai
ii
i
AVF
n
n
n
n
1)1(
)1(
)1(
1)1( −+
=+
+
−+
=
1)1( −+
= n
i
i
VFVA

27. Si usted compra un automóvil de $40,000,000 con una cuota
inicial del 20%, con el saldo a 60 meses al 1% mensual, cuál es
el monto de las cuotas mensuales?
P = $40,000,000 menos la cuota inicial = $32,000,000
i = 1% mensual
n = 60 meses
A (cuota) =
Interés Compuesto
33.822,711$
1)01.01(
)01.01(01.0
*000,000,32$ 60
60
=
−+
+

28. Si ahorra mensualmente $700,000 en una corporación que le
ofrece un rendimiento mensual del 0.7%, cuánto tendrá en
dos años?
A = $700,000
i = 0.7% mensual
n = 24 meses
F = A((1+i)n
– 1)/i =
Interés Compuesto
55.447,224,18$
007.0
1)007.01(
*000,700$
24
=
−+

29. Estudiemos ahora el caso cuando los flujos aumentan en un
porcentaje cada período. Se le llama gradiente geométrico.
Interés Compuesto
1 2 3 4 5 n
B
B(1+j)
b(1+j)2
b(1+j)3
b(1+j)4
b(1+j)n-1

30. Interés Compuesto








−





+
+
−
=








−





+
+
=





−
+
+
=−






−
+
+
+
=





+
−
+
+
=
+
−
+
−
=





+
+−+
=





+
+
−
+
+
=





−
+
+






+
−
+
+
=−
+
+
=−






+
+
++
+
+
+
+
+
+
+
+
=
+
+






+
+
++
+
+
+
+
+
+
++
+
=
+
+






+
+
++
+
+
+
+
+
+
+
=
+
+
++
+
+
+
+
+
+
+
=
+
+
+
−
−
−
1
)1(
)1(
)(
1
)1(
)1(
1
)1(
)1(
)(
1
)1(
)1(
)1(
1
)1(
1
)1(
)1(
)1(
)(
)1(
)(
)1(
)1()1(
)1(
)1(
)1(
)1(
1
)1(
)1(
)1(
1
)1(
)1(
)1(
)1(
1.2.
.2.
)1(
)1(
...
)1(
)1(
)1(
)1(
)1(
)1(
)1(
)1(
)1(
)1(
...
)1(
)1(
)1(
)1(
)1(
1
)1(
)1(
)1(
)1(
.1.
)1(
)1(
...
)1(
)1(
)1(
)1(
)1(
1
)1(
)1(
...
)1(
)1(
)1(
)1(
)1(
1
1
14
3
3
2
2
1
3
2
2
1
3
2
2
1
3
2
2
n
n
n
n
n
n
n
n
n
n
n
n
n
n
n
n
n
n
i
j
ij
B
VP
i
j
B
i
j
BijVP
i
j
i
B
ii
j
B
i
ij
VP
i
ij
VP
i
ij
VP
i
i
i
j
VP
i
j
VP
ii
j
BVP
i
j
VPecec
ec
i
j
i
j
i
j
i
j
B
i
j
VP
i
j
i
j
i
j
ii
j
B
i
j
VP
ec
i
j
i
j
i
j
i
BVP
i
jB
i
jB
i
jB
i
B
VP

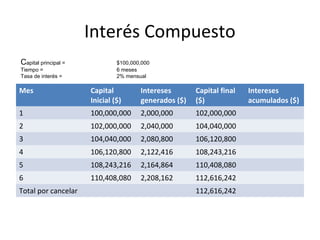
31. Ejemplo:
Calcular el valor del préstamo cuya primera cuota es de
$100,000 que aumenta en un 1% mensual y que tiene como
tasa de interés 2% mensual a 12 meses.
B = 100,000; i = 0.02; j = 0.01; n = 12
VP = B/(j-i) * {[(1+j)/(1+i)]n
-1}
VP = 100,000/(0.01-0.02)*{[(1+0.01)/(1+0.02)]n
-1}
VP = $1,115,062
Interés Compuesto

32. En el caso de proyectos que no tienen caducidad, el tiempo
podría ser infinito por lo cual se requiere saber el valor
presente de una serie infinita de flujos. En principio
supongamos que dichos flujos son iguales:
Interés Compuesto
( )
i
A
VP
i
A
i
A
ii
A
VP
ii
A
VP
ii
i
i
A
i
i
i
A
ii
i
AVP
n
n
n
nn
n
n
n
n
n
=
−=





∞
−=





+
−=






+
−=






+
−
+
+
=





+
−+
=
+
−+
=
∞→
∞∞→ 01
1
1
)1(
1
1
)1(
1
1
)1(
1
)1(
)1(
)1(
1)1(
)1(
1)1(

33. ¿Cuál es el valor presente del costo de mantenimiento y
actualización ($4,000,000 anuales) que cobra una empresa de
desarrollo por un aplicativo a su cliente suponiendo que el
cliente lo usará indefinidamente y que el costo de
oportunidad de la empresa es del 15% anual?
VP = A/i = $4,000,000 / 0.15 = $26,666,667
Interés Compuesto

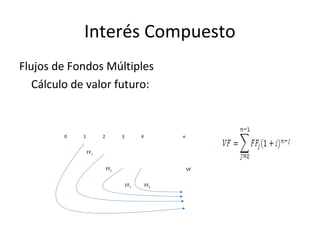
34. Igualmente, se puede aplicar la teoría a gradientes
geométricos infinitos.
Interés Compuesto
[ ]
[ ] ∞=−∞
−
=








−





+
+
−
=
<
−
=−
−
=








−





+
+
−
=
>








−





+
+
−
=
∞
∞→
∞
∞→
1
)(
1
)1(
)1(
)(
,
)(
10
)(
1
)1(
)1(
)(
,
1
)1(
)1(
)(
ij
B
i
j
ij
B
VP
jiSi
ji
B
ij
B
i
j
ij
B
VP
jiSi
i
j
ij
B
VP
n
n
n

35. Igualmente, se puede aplicar la teoría a gradientes
geométricos infinitos.
Interés Compuesto
)1()1(
)1(
1
...
)1(
1
)1(
1
)1(
1
)1(
)1(
...
)1(
)1(
)1(
)1(
)1(
1
)1(
)1(
...
)1(
)1(
)1(
)1(
)1(
,
1
3
2
2
1
3
2
2
i
nB
i
n
BVP
iiii
BVP
i
i
i
i
i
i
i
BVP
i
jB
i
jB
i
jB
i
B
VP
jisi
n
n
n
n
+
=





+
=






+
++
+
+
+
+
+
=






+
+
++
+
+
+
+
+
+
+
=
+
+
++
+
+
+
+
+
+
+
=
=
−
−

36. ¿Cuál es el valor presente del costo de mantenimiento
($4,000,000 anuales que sube con el IPC anualmente) que
cobra una empresa de desarrollo por un aplicativo a su cliente
suponiendo que el cliente lo usará indefinidamente y que el
costo de oportunidad de la empresa es del 15% anual?
Suponga un IPC del 4,5%.
VP = B/(i-j) = $4,000,000 / (0.15-0.045) = $38,095,238
Interés Compuesto

37. Plazo Muerto
Periodo en el cual no se hacen pagos ni se contabilizan
intereses pero si se toma en cuenta el tiempo transcurrido del
plazo muerto dentro del plazo total del préstamo.
Interés Compuesto
1)1(
)1(
−+
+
=
−
−
PMn
PMn
i
ii
PVA

38. Periodo de Gracia
Período en el cual no se hacen pagos pero sí se contabilizan
intereses. Igualmente el tiempo transcurrido de gracia cuenta
en el tiempo total.
Interés Compuesto
1)1(
)1(
1)1(
)1(
)1(
−+
+
=
−+
+
+=
−
−
−
PGn
n
PGn
PGn
PG
i
ii
PVA
i
ii
iPVA

39. Amortización
Fórmulas:
INTt = SIt * i
ABt = Ct – INTt
SFt = SIt – ABt
SIt+1 = SFt
donde:
INTt = Monto de los intereses del período t
ABt = Abono a capital período t
Ct = Monto de pago o cuota período t
SIt = Saldo inicial del período t
SFt = Saldo final del período t
i = Tasa de interés a aplicar en cada período

40. Ejemplo en Excel (alicuota):
Amortización
P 100,000,000
i 30%
n 5
Periodo Saldo ini intereses capital cuota saldo fin
1 100,000,000 30,000,000 11,058,155 41,058,155 88,941,845
2 88,941,845 26,682,554 14,375,601 41,058,155 74,566,244
3 74,566,244 22,369,873 18,688,282 41,058,155 55,877,962
4 55,877,962 16,763,389 24,294,766 41,058,155 31,583,196
5 31,583,196 9,474,959 31,583,196 41,058,155 0

41. Ejemplo en Excel (gradiente geométrico):
Amortización
P 100,000,000
i 30%
j 10%
n 5
Periodo Saldo ini intereses capital cuota saldo fin
1 100,000,000 30,000,000 5,320,535 35,320,535 94,679,465
2 94,679,465 28,403,839 10,448,750 38,852,589 84,230,715
3 84,230,715 25,269,215 17,468,633 42,737,848 66,762,082
4 66,762,082 20,028,625 26,983,008 47,011,633 39,779,074
5 39,779,074 11,933,722 39,779,074 51,712,796 0

42. Tasas de interés

43. Denominaciones de la Tasa de Interés
Según como proponga la información de los
períodos de tiempo:
• Periódica – corresponde al periodo de composición (día, mes,
trimestre, etc.)
• Nominal – la expresión anualizada de la tasa periódica, es
decir, la tasa periódica multiplicada por el número de
períodos al año
• Efectiva – la expresión equivalente a una tasa periódica pero
con período igual a un año

44. Denominaciones de la Tasa de Interés
Según la causación:
• Anticipada – cuando el interés se causa en forma anticipada
en el período.
• Vencida - cuando el interés se causa en forma vencida en el
período. La tasa efectiva solamente se expresa como vencida.

45. Ejemplos de Tasas de Interés
Tasa periódica:
2% m.v.
2% mes vencido, es decir, paga de interés el 2% del valor
prestado al final de cada mes.
3% t.a.
3% trimestre anticipado, es decir, paga anticipadamente el
3% del valor prestado cada tres meses empezando desde el
mes cero.

46. Ejemplos de Tasas de Interés
Tasa nominal:
24% a.m.v.
24% anual compuesto mensualmente causado al final del
mes, es decir, equivalente al 2% m.v. de la página anterior
(2%*12)
12% a.t.a.
12% anual compuesto trimestralmente con pago anticipado,
equivalente al 3% t.a. anterior (3%*4).

47. Ejemplos de Tasas de Interés
Tasa efectiva:
Fórmulas de conversión de tasas periódicas y nominales a
efectivas:
de periódica anticipada a periódica vencida: ipv= ipa/(1-ipa)
de periódica vencida a periódica anticipada: ipa= ipv/(1+ipv)
de periódica vencida a efectiva: ie = (1 + ipv)n
– 1
de efectiva a periódica vencida: ipv = (1 + ie)1/n
– 1

48. Ruta de Equivalencia de Tasas
m periodos por año ñ periodos por año
inv ipv ie ipv inv
ina ipa ipa ina
ipv=ipa/(1-ipa) ipa=ipv/(1+ipv)
ipa=ina/m
inv=ipv*ñ
ina=ipa*ñ
ie=(1+ipv)m
-1 ipv=(1+ie)1/ñ
-1ipv=inv/m

49. Ejemplos de Tasas de Interés
Tasa efectiva:
24% a.m.v. = 24% / 12 m.v. = 2% m.v. = (1 + 2%)12
- 1 e.a. =
(1.02)12
– 1 = 0.2682 = 26.82% e.a.
12% a.t.a. = 12% / 4 t.a. = 3% t.a. = 3% / (1 – 3%) t.v. =
0.03/0.97 t.v. = 0.0309 t.v. = 3.09% t.v. = (1 + 3.09%)4
-1 e.a. =
(1.0309)4
– 1 e.a. = 0.1296 e.a. = 12.96% e.a.

50. Tasa real
Tasa de interés sobre moneda constante, es
decir, libre del efecto de la inflación.
Fórmula: iR = (1 + ie) / (1 + if) - 1
Ejemplo 1: 20% e.a. con inflación del 5% e.a.
Tasa real = (1 + 20%)/(1 + 5%) -1 = 14.29% e.a.

51. Tasa real
Ejemplo 2
Hoy
Tengo : $10,000
Precio panela : $100
Puedo comprar : 100 panelas
Inflación = 5% e.a.
Tasa inversión = 20% e.a.
En un año
Tengo : $10,000*(1+20%)=$12,000
Precio panela : $100*(1+5%)=$105
Puedo comprar : $12,000 / $105 = 114.29 panelas

52. Tasas Mixtas
Una tasa es mixta cuando se declara como la suma
de dos tasas, generalmente una variable o de
referencia y una fija.
Las dos tasas deben referirse al mismo período antes
de sumarse. Normalmente se acepta como guía la
declaración de la fija a menos que ésta no se defina y
en ese caso se toma la declarada por la variable.

53. Ejemplo:
DTF + 5% a.t.v. (si el DTF está en 7% ea)
1)Pasar la DTF a a.t.v.
7% e.a. -> (1+7%)(1/4)
-1 t.v.=1.706% t.v.=6.823% a.t.v.
2)Sumar las tasas
6.823% + 5% = 11.823% a.t.v.
3)Pasar la tasa a efectiva anual para comparación:
11.823% a.t.v. -> 2.956% t.v. -> (1+2.956%)4
-1 e.a. = 12.358% e.a.
Otras tasas de referencia: Libor, Prime rate
Tasas Mixtas

54. Tasas Compuestas
Cuando la tasa se define entre dos o más tasas y una de ellas
se declara sobre una base monetaria diferente a la base de
declaración de la tasa original.
Fórmula: i = (1 + iu)(1 + ic) - 1
Ejemplo 1: Inversión que gana 9% e.a. en dólares – tasa
equivalente en pesos si la devaluación es del -2% e.a.
i = (1 + 9%)(1 – 2%) – 1 = 6.82% e.a.

55. Tasas Compuestas
Ejemplo 2:
Hoy:
Tengo : $100,000,000 COP
TRM : $2,500 COP/USD
Compro: $40,000 USD
Tasa inversión USD : 9% e.a.
Devaluación : -2% e.a.
En un año:
Tengo : $40,000*(1+9%) = $43,600 USD
TRM: $2,500*(1-2%) = $2,450 COP/USD
Compro : $43,600*2,450 = $106,820,000 COP
Utilidad : ($106,820,000 / $100,000,000 )-1 = 6.82%