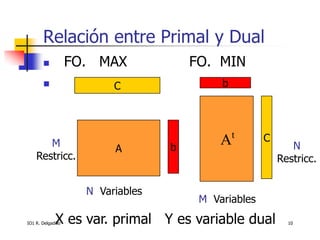
La teoría de dualidad introduce el concepto de que todo problema de optimización lineal tiene un problema dual asociado. Describe las dualidades simétrica, asimétrica y mixta y sus propiedades clave, incluida la relación entre las variables primal y dual. Además, explica la interpretación económica de los precios sombra en el problema dual.