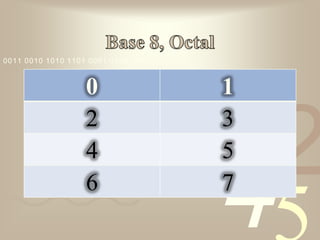
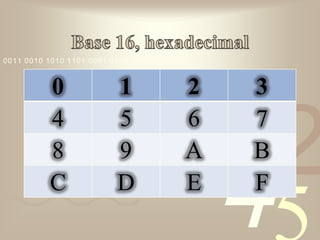
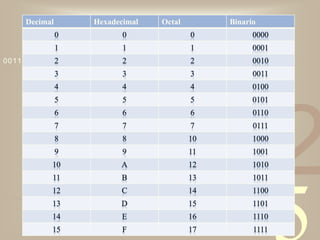
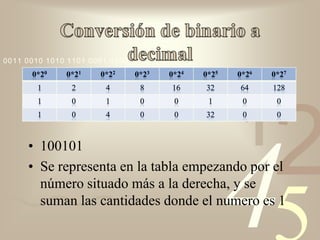
El documento describe diferentes sistemas de numeración como el decimal, binario y hexadecimal. Explica que cada sistema utiliza símbolos diferentes y que el valor de cada símbolo depende de su posición. También cubre cómo convertir entre sistemas de numeración usando métodos como divisiones sucesivas o descomponer en potencias de la base.

1. 0011 0010 1010 1101 0001 0100 1011
1
2
4
Conrado Perea

2. 0011 0010 1010 1101 0001 0100 1011
• Un sistema de numeración es una forma de
representar cualquier cantidad numérica.
1
2
• Casi todos los sistemas de numeración son
de tipo polinomial y cumplen las siguientes
4
características:

3. 0011 0010 1010 1101 0001 0100 1011
• Todo número es una expresión formada por
un conjunto de símbolos. Cada uno tiene un
1
2
valor fijo y diferente a los demás.
• El número de símbolos distintos que se
4
pueden usar en un determinado sistema de
numeración constituye su base.

4. 0011 0010 1010 1101 0001 0100 1011
0 1
1
2
4

5. 0011 0010 1010 1101 0001 0100 1011
0 1
2 3
1
2
4
4 5
6 7

6. 0011 0010 1010 1101 0001 0100 1011
0 1
2 3
1
2
4
4 5
6 7
8 9

7. 0011 0010 1010 1101 0001 0100 1011
0 1 2 3
4 5 6
1
7
2
4
8 9 A B
C D E F

8. Decimal Hexadecimal Octal Binario
0 0 0 0000
1 1 1 0001
2 2
0011 0010 1010 1101 0001 0100 1011 2 0010
3 3 3 0011
4 4 4 0100
5 5 5 0101
1
2
6 6 6 0110
7 7 7 0111
8 8 10 1000
4
9 9 11 1001
10 A 12 1010
11 B 13 1011
12 C 14 1100
13 D 15 1101
14 E 16 1110
15 F 17 1111

9. 0011 0010 1010 1101 0001 0100 1011
• El valor numérico que expresa una
determinada combinación de dígitos en una
base de numeración dada, depende de dos
factores:
1. El valor de los dígitos 1
2
polinomio.
4
2. La posición de cada uno de ellos en el
Cada posición del dígito tiene un valor intrínseco
que aumenta de derecha a izquierda.

10. 0011 0010 1010 1101 0001 0100 1011
• Procedentes de los árabes, sustituyó a la
numeración romana, y es el habitual en la vida
cotidiana.
1
2
• También se conoce como en base 10 porque
emplea 10 símbolos para representar los números.
4
– 0123456789
• Un número se descompone en potencias de 10,
ejemplo
• 5478=5x103+ 4x10 2+7x101+8x10 0

11. 0011 0010 1010 1101 0001 0100 1011
• Este sistema es el utilizado internamente por los
circuitos digitales.
2
• Se denomina base 2 por que emplea dos símbolos
para representar los números: 0 1
1
• Cada cifra o dígito de un número representado en
4
este sistema es conocido como BIT
• 1101= 1x23+1x22+0x21+1x20.

12. 0011 0010 1010 1101 0001 0100 1011
• Se llama conversión entre números
representados en distintos sistemas de
1
2
numeración a la trasformación de una
determinada cantidad expresada en uno de
4
dichos sistemas de numeración en su
representación equivalente en el otro sistema.

13. 0011 0010 1010 1101 0001 0100 1011
• Método: hacer divisiones
sucesivas entre dos hasta
que el cociente en una de
las divisiones tome el
1
2
valor 0. La unión de todos
los restos obtenidos,
escritos en orden inverso,
4
nos proporciona el número
inicial en binario.
• Ejemplo 10=1010B
• Ejercicio a realizar 145 en
binario.

14. 0011 0010 1010 1101 0001 0100 1011
1
2
4

15. 0011 0010 1010 1101 0001 0100 1011
• MÉTODO: descomponer el número en potencias
de 2.
• EJEMPLO: 100101
1
2
– 1x25+0x24+0x23+1x22+0x21+1x20=1x32+0x16+0x8+1
x4+0x2+1x1=37 Por lo tanto 100101B=37
4
• EJEMPLO 10011001 a decimal
– 1x27+0x26+0x25+1x24+1x23+0x22+0x21+1x20=1x128+
0x64+0x32+1x16+1x8+0x4+0x2+0x1=128+16+8+1=1
53
– Ejercicio a realizar 111100001010

16. 0011 0010 1010 1101 0001 0100 1011
0*20 0*21 0*22 0*23 0*24 0*25 0*26 0*27
1 2 4 8 16 32 64 128
1 0 1 0 0 1 0 0
1
2
1 0 4 0 0 32 0 0
• 100101
• Se representa en la tabla empezando por el
número situado más a la derecha, y se
suman las cantidades donde el numero es 1
4

17. 0011 0010 1010 1101 0001 0100 1011
0*20 0*21 0*22 0*23 0*24 0*25 0*26 0*27
1 2 4 8 16 32 64 128
0 2 6 6 22 22 22 150
1
2
0 1 1 0 1 0 0 1
• 150
4
• Empezamos restando 128 al número que
queremos convertir, si se puede realizar la
operación ponemos 1 de lo contrario
ponemos un 0 y seguimos sucesivamente.
• El resultado se representa en orden inverso.