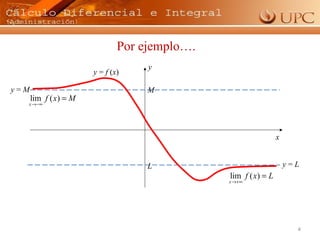
El documento trata sobre límites al infinito de funciones. Explica que un límite al infinito indica a qué valor se aproxima una función cuando su variable independiente crece o decrece indefinidamente. Para funciones polinómicas y racionales, el límite depende del término de mayor grado. También analiza límites infinitos cuando una función aumenta o disminuye sin límite, y cómo calcular límites a partir de una gráfica.

1. Unidad 1 : Funciones, Límite y Continuidad Límites al infinito Límites infinitos

2. ¿Cuál es el máximo número esperado de clientes al cual se tiende en el largo plazo ? Analicemos … ¿ ? 50 Esto es un límite al infinito , que nos indica a qué valor se aproxima la función cuando t crece indefinidamente. tiempo (años) clientes f ¿ ? Entonces:

3. Límites al infinito Si los valores de la función f ( x ) tienden al número L cuando x aumenta indefinidamente, se escribe: De manera similar, valores de la función f ( x ) tienden al número M cuando x disminuye indefinidamente, se escribe:

4. Por ejemplo…. y = f ( x ) y y = L y = M M L x

5. límite al infinito para funciones polinómicas Es decir, para hallar el límite de un polinomio en el infinito, se halla el límite del término de mayor grado (término dominante). Ejemplos: a) b)

6. Interrogante . . . . . Sabemos que para n > 0, , ¿cuál es el valor de los siguientes límites?

7. Divida el numerador y denominador entre el x elevado al mayor grado del denominador y calcule el límite de la nueva expresión: Resolución: límite al infinito para funciones racionales

8. Para funciones racionales: Resolución simplificada: Calcular el límite, tomando en cuenta el término dominante del numerador y del denominador:

9. Ejercicios: 1. 2. 3. 4. Calcule los siguientes límites

10. Problema Si se siembra cierto cultivo en una tierra donde el nivel de nitrógeno es N , entonces el volumen de la cosecha Y puede modelarse con la función de Michaelis – Menten: donde A y B son constantes positivas. ¿Qué le sucede a la cosecha cuando el nivel de nitrógeno se incrementa indefinidamente?

11. Límites infinitos Se dice que es un límite infinito si f ( x ) aumenta o disminuye ilimitadamente cuando x -> a. Técnicamente, este límite no existe, pero se puede dar más información acerca del comportamiento de la función escribiendo: si f ( x ) crece sin límite cuando x -> a. si f ( x ) decrece sin límite cuando x -> a.

12. ¡Interrogante! A partir de la gráfica . . . , ¿ en qué valor de a , se cumple:

13. a. Estime Ejemplo 1: b. Estime . ¿A dónde tiende ? ¿A dónde tiende cuando x tiende a −1?

14. De la gráfica de la función f , halle en caso exista, los siguientes límites: Ejemplo 2:

15. Esboce el gráfico de una función f con dominio R que cumpla con las siguientes condiciones: Ejemplo 3: