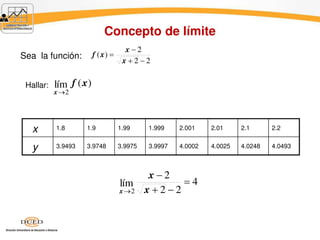
Este documento presenta información sobre límites de funciones. Introduce el concepto de límite de una función y cómo evaluar el comportamiento de una función cuando el valor de la variable independiente se aproxima a un número particular. Explica límites laterales, límites al infinito y límites infinitos. Proporciona ejemplos y ejercicios para ilustrar los diferentes tipos de límites.

1. Módulo: I Unidad: I Semana: 03
ANÁLISIS MATEMÁTICO
Lic. Segundo A. García Flores

2. TÍTULO DEL TEMA
LÍMITE DE UNA FUNCION

3. ORIENTACIONES
• Lea las previamente las orientaciones generales
del curso.
• Revise los temas afines a este en la Biblioteca
Virtual de la UAP
• Participe de los foros.
• Tenga a la mano una lista de las propiedades de
limites, será muy útil para el cálculo.

4. CONTENIDOS TEMÁTICOS
Límite de una función
Limites laterales
Limites infinitos

5. DESARROLLO DE CONTENIDOS - SUBTÍTULOS
DEL TEMA

6. LÍMITE DE UNA FUNCION
Consideremos la función:
x x
1
3



x
y
evaluaremos el comportamiento de la función, según valores asignados:
x 0 0.5 0.8 0.9 0.99 0.999 0.9999
y 0 0.75 1.44 1.71 1.9701 1.9970 1.9997
x 2 1.5 1.2 1.1 1.01 1.001 1.0001
y 6 3.75 2.64 2.31 2.0301 2.0030 2.0003

7. Evaluación de la función
1.- en el 1º cuadro, ¿a qué número se aproximan “x” e “y”?
cuando “x” se aproxima lo más cercano posible a 1
por la izquierda, el valor de “y”, tiende a 2.
2.- en el 2º cuadro, ¿a qué número se aproximan “x” e “y”?
cuando “x” se aproxima lo más cercano posible a 1
por la derecha, el valor de “y”, tiende a 2.

8. Concepto de límite
Si f(x) se acerca arbitrariamente a un número l, conforme “x”
se aproxima a un número “a” tanto por la izquierda como por
la derecha, entonces “l” es el límite de f(x) cuando “x” tiende
a “a”. Denotándose como:
f x L
lím ( )
x a



9. 2

2 2
( )
x
 

x
f x
lím ( )
2
f x
x
x 1.8 1.9 1.99 1.999 2.001 2.01 2.1 2.2
y 3.9493 3.9748 3.9975 3.9997 4.0002 4.0025 4.0248 4.0493
4
2

2 2
lím
2

x
 
 x
x
Sea la función:
Hallar:
Concepto de límite

10. 4
3
2
1
2

x
-2 -1 1 2 3 4 5
x
y
4
2 2
lím
2

 
 x
x

11. Ejemplo:
f (x)  4x 7
Sea la función f definida por:
A) Utilizando un gráfico, para , determinar un (delta) tal que si
  0.01   0
0 < | x – 3 | < δ ; entonces | f (x) – 5 | < 0.01
B) Usando las propiedades de desigualdades, determinar un į > 0 tal que si 0 < | x – 3
| < į; entonces | f (x) – 5 | < 0.01
lím ( ) 5
3


f x
x
5.01
5
4.99
3
x1 x2
f (x) =4 x - 7
(2.9975) (3.0025)

12. solución a:
4 x1 - 7 = 4.99 4 x2 – 7 = 5.01
2.9975 x  
11.99
x  
4
1
como 3 – 2.9975 = 0.0025
y 3.0025 – 3 = 0.0025
3.0025
12.01
4
2
se elige į = 0.0025, de tal forma que
0 < | x-3| < 0.0025 | f (x) – 5 | < 0.01

13. solución b:
para toda İ > 0 y į > 0, se debe cumplir que:
0  x  a   f (x)  L 
donde a = 3, l = 5 y f (x) = 4 x – 7, e = 0.01, entonces:
0 < | x - 3 | < į sí y sólo sí | (4x – 7) - 5 | < 0.01
tomando la segunda ecuación:
| (4x – 7) - 5 | < 0.01
| 4x – 7 - 5 | < 0.01
| 4x – 12 | < 0.01
| 4 (x – 3 ) | < 0.01
| 4 | | x – 3 | < 0.01
4 | x – 3 | < 0.01
0.01
4
x 3 

14. si tomamos
entonces:
0.01

  
0 < |x - 3 | < į sí y solamente sí | (4x – 7) - 3 | < İ
es correcto, puesto que:
0 < | x - 3 | < 0.0025
4 | x - 3 | < 4 ( 0.0025 )
| 4 (x – 3) | < 0.01
| 4x - 12 | < 0.01
| ( 4x – 7) - 5 | < 0.01
| f (x) - 5 | < 0.01
0.0025
4
4


15. Límite por la derecha
f x
Decimos que tiene un límite por la derecha L en x0, y
escribimos
f x L
  0
lim
x x
Si para cada número  > 0 existe un número  > 0 tal que
para toda x
x0 < x < x0 +  | f(x) – L | < 

16. Límite por la izquierda
Decimos que f(x) tiene un límite por la izquierda L en x0, y
escribimos:
f x M
  0
lim
x x
Si para cada número  > 0 existe un número  > 0 tal que para
toda x
x0 –  < x < x0 | f(x) – M | < 

17. Interpretación geométrica

18. Ejemplos
1. Calcular si existe
 2
 
 
  
1
3 si 1
x x
lim f ( x ), donde: f ( x
)
x  x 1 si x
1
2. Calcular si existe
 2

 
  
2
si 2
x x
lim f ( x ), donde: f ( x
)
x  8 2 x si x
2

19. 3.En el siguiente gráfico hallar:
lim f ( x ), lim f ( x
)
x x
 
1 2

20. clientes
Límites al infinito y límites infinitos
50
t
                  
tiempo
(años)










f
¿Cuál es el máximo número esperado de
clientes al cual se tiende en
el largo plazo?
Análisis del límite al infinito:
¿ ?
¿ ?
Entonces:
Esto es un límite al infinito, que nos indica a qué valor se
aproxima la función cuando t crece indefinidamente.

21. Límites al infinito
Si los valores de la función f (x) tienden al número L
cuando x aumenta indefinidamente, se escribe:
lim ( )
x
f x L


De manera similar, valores de la función f (x) tienden
al número M cuando x disminuye indefinidamente,
se escribe:
lim ( )
x
f x M



22. y = f (x)
y
y = L
y = M M
L
lim ( )
x
f x L


lim ( )
x
f x M


x
Por ejemplo….

23. límite al infinito para funciones polinómicas
n n f x a x a x a x a 
  1
  
 1 1 0 ( ) n n
  
lim f ( x ) lim a x
n
n
 
x x
Es decir, para hallar el límite de un polinomio en el
infinito, se halla el límite del término de mayor grado
(término dominante).
Ejemplos:
a) 3 2 59
lim
x x
x 
3 6
     
b) ( 5) 4 2 lim    

x x x
x

24. Sea n, un número entero positivo cualquiera entonces
se cumple:
24
1 iii ) lim x
n
 
x

) lim 0 n
x x
i


1
) lim 0 n
x x
ii


Teorema.-
Ejemplo:
2
 
 
2 x 3 x
5
2
)
3 2 1 lim
x
a
 x x
2
 

2 3 5
4
)
2
lim
x
x x
b
 x
2
) lim( 5 6 )
c x x x
x

  
2
) lim( 2 4 )
d x x x
x

  
 x 3 x
2

    2
  
)
2 2 lim
x
e
 x x
3 3
) lim( 1 )
d x x
x

 

25. límite al infinito para funciones racionales

 1
  
a x a x a x a

1 1 0

1
1 1 0
( )
n n
n n
m m
m m
f x
b x b x b x b


   
Divida el numerador y denominador entre el x elevado
al mayor grado del denominador y calcule el límite de
la nueva expresión:
 a x  a x 
1
  a x  a

 1 1 0

  
  1
   1 1 0

 
lim ( ) lim
n n
n n
m
m m
x x
m m
m
f x x
b x b x b x b
x

  

Resolución:

26. 
   
a x a x a x a
26
Para funciones racionales:
1

1 1 0

1
1 1 0
( )
n n
n n
m m
m m
f x
b x b x b x b


   
Resolución simplificada:
Calcular el límite, tomando en cuenta el término
dominante del numerador y del denominador:
m
a x
m
n
n
lim

x b x

27. 27
Ejercicios:
Calcule los siguientes límites
2

4 x
5
lim 2

2 3
 x
x

3 4
x x
x
lim 
x 
1 2

3 4
x x
x
lim 
x 
1 2
7
3

x
lim 2 
 x
x
1.
2.
3.
4.

28. Problema
Si se siembra cierto cultivo en una tierra donde el nivel
de nitrógeno es N, entonces el volumen de la cosecha Y
puede modelarse con la función de Michaelis – Menten:
28
AN
 
( ) 0
Y N N

B N
donde A y B son constantes positivas. ¿Qué le sucede a
la cosecha cuando el nivel de nitrógeno se incrementa
indefinidamente?

29. lim ( )
x a
Se dice que es un límite infinito si f (x)
aumenta o disminuye ilimitadamente cuando x→a.
Técnicamente, este límite no existe, pero se puede
dar más información acerca del comportamiento
de la función escribiendo:
29
Límites infinitos
lim f ( x
)
x a

 
f x

lim f ( x
)
x a

  si f (x) crece sin límite cuando x→a.
si f (x) decrece sin límite cuando x→a.

30. 30
Ejemplo
A partir de la gráfica . . . , ¿en qué valor de a, se cumple:
 
lim f (x)
x a


31. 31
1 1
a. Estime lim , lim
x     2  2
1 x 1  x  1
 x 
1
 Ejemplo 1:
¿A dónde tiende cuando x tiende a −1?  2
2 2
b. Estime lim , lim
.
   x 2 x  2 x  2
x  2 ¿A dónde tiende ?
2
2
lim
x x  2
1
( )
1
f x
x



32. 32
Ejemplo 2:
De la gráfica de la función f, halle en caso exista, los
siguientes límites:

33. CONCLUSIONES Y/O ACTIVIDADES DE
INVESTIGACIÓN SUGERIDAS
Se recomienda complementar lo expuesto con la revisión y análisis del
material bibliográfico contenido en los siguientes enlaces:
Análisis de funciones en economía y empresa
http://books.google.com.pe/books?id=Rk3ImXQqp7QC&pg=PA151&dq=
LIMITES+DE+FUNCION&lr=lang_es&as_brr=3&as_pt=BOOKS&cd=2#v=
onepage&q=&f=false
Cálculo Infinitesimal: Límite Y Continuidad De Funciones
http://books.google.com.pe/books?id=DEW2TeAjhhYC&pg=PA249&dq=
LIMITES+DE+FUNCION&lr=lang_es&as_brr=3&as_pt=BOOKS&cd=5#v=
onepage&q=&f=false

34. GRACIAS