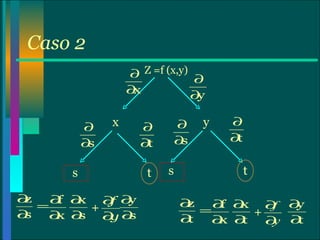
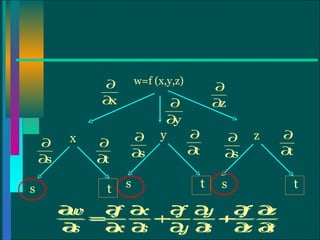
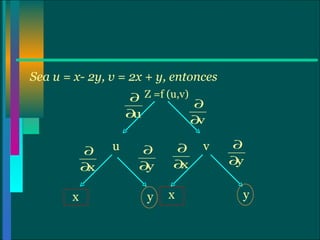
El documento explica las reglas de la cadena para funciones de varias variables. Presenta varios casos de la regla de la cadena, incluyendo funciones de dos y más variables donde las variables dependen de otras variables. También cubre conceptos como la derivada segunda, la ecuación de Laplace y la derivación implícita.