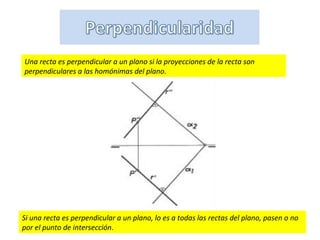
Una recta es perpendicular a un plano si sus proyecciones son perpendiculares a las del plano, y si es perpendicular a un plano, lo es a todas las rectas dentro de él. Según el teorema de las tres perpendiculares, si dos rectas son perpendiculares en el espacio y una es paralela o está contenida en un plano de proyección, ambas se proyectan como perpendiculares. Esto implica que si una recta es perpendicular a un plano, sus proyecciones serán perpendiculares a las trazas del mismo.

1. Una recta es perpendicular a un plano si la proyecciones de la recta son
perpendiculares a las homónimas del plano.
Si una recta es perpendicular a un plano, lo es a todas las rectas del plano, pasen o no
por el punto de intersección.

2. Teorema de las tres perpendiculares
Si dos rectas R y S son perpendiculares en el espacio, y una de ellas, la R por
ejemplo, es paralela a un plano de proyección ( b ) o está contenida en él ( c ),
ambas rectas se proyectan perpendiculares sobre dicho plano.

3. Perpendicularidad entre recta y plano
Si una recta es perpendicular a un plano lo es a todas sus rectas, por tanto, si la recta R es
perpendicular al plano (P), lo es a su traza P.
Por el teorema de las tres
perpendiculares, siendo R y P
perpendiculares y estando contenida
la traza P del plano en el plano de
proyección, las proyecciones de R y P
deben mostrarse ortogonales.
De lo dicho deducimos que si una recta es
perpendicular a un plano, sus proyecciones son
perpendiculares a las trazas de dicho plano.