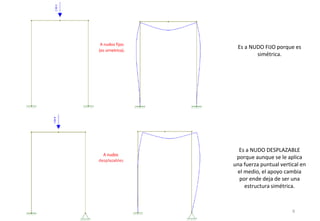
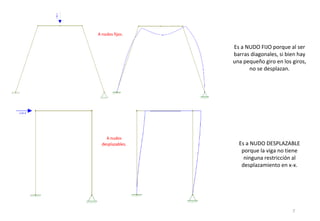
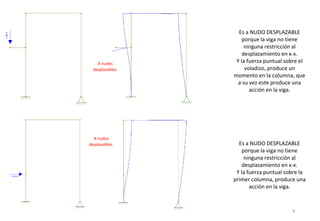
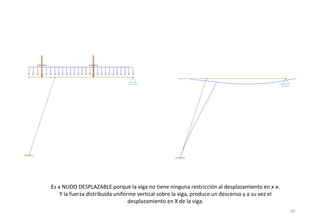
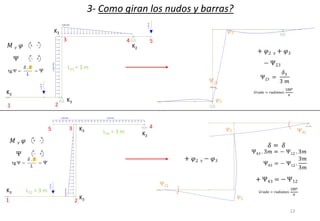
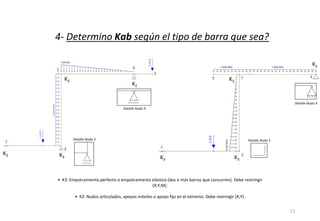
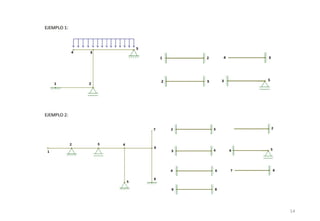
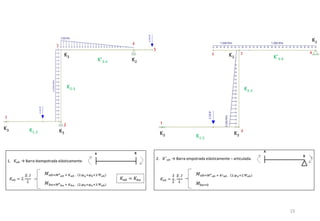
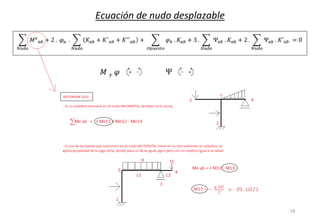
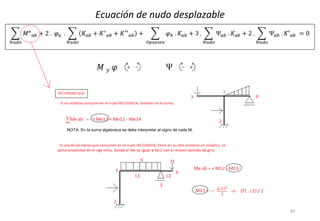
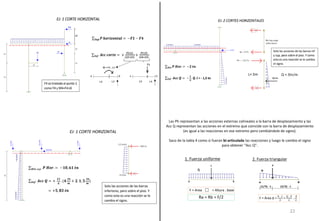
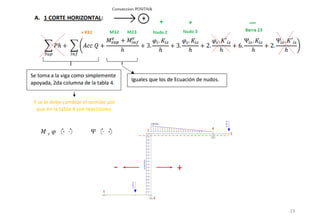
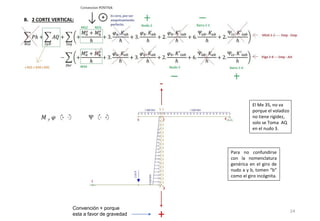
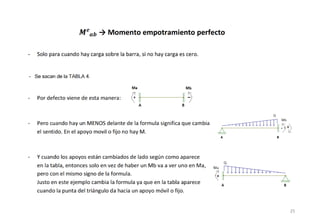
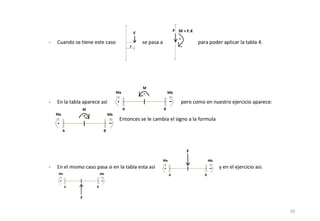
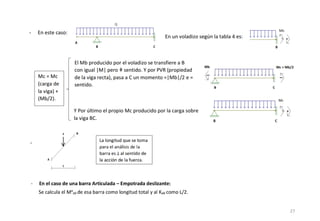
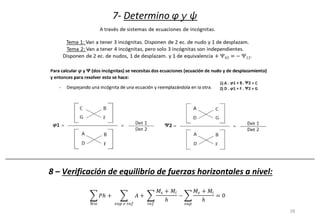
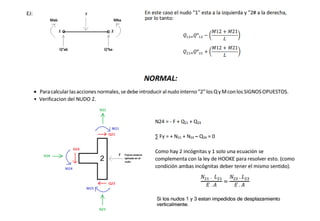
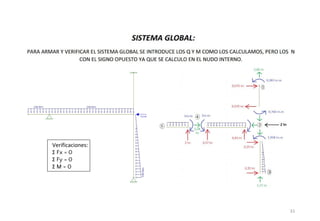
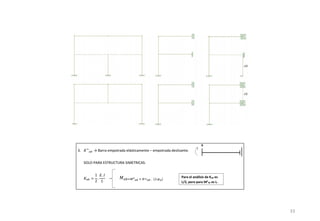
El método de las deformaciones resuelve los esfuerzos internos en una estructura determinando los giros de nudos y barras. Esto se logra estableciendo ecuaciones de equilibrio para la estructura. Las incógnitas son las deformaciones (giros de nudos y barras), las cuales se determinan resolviendo el sistema de ecuaciones. El método consiste en verificar el tipo de nudo, cortar la estructura, determinar giros y desplazamientos, establecer ecuaciones de equilibrio y obtener diagramas de esfuerzos.

1. 1

2. Para que sirve el método de las
deformaciones?
2
El método de las deformaciones resuelve los esfuerzos internos en las barras
de una estructura, en función de los giros de nudos y de barras a determinar,
que se obtienen planteando ecuaciones de equilibrio de la estructura.
Mas precisamente resuelve los momentos finales en los extremos de c/u de
las barras que dependen justamente de los giros de sus nudos extremos y del
giro de la barra.
“Las incógnitas a determinar son deformaciones (giros de nudos y de barras)”.

3. 1) Ver si es una estructura a nudo fijo o desplazable
2) Ver en que plano cortar la estructura según su desplazamiento y como mirarla.
3) Ver que nudos y barras se giran y se desplazan y su signo correspondiente.
4) Determino Kab y sus Me
ab.
5) Ecuación de nudo.
6) Ecuación de desplazamiento.
7) Determino ϕ y ψ a través de sistema de ecuaciones de incógnitas.
8) Verificación de equilibrio de fuerzas horizontales a nivel.
9) Ecuación de barra (Mab)
10) Verificaciones ΣM = 0 ; ΣFh = 0 ; ΣFv = 0 de cada barra.
11) Esfuerzo de corte (Qab)
12) Esfuerzos normales
13) Diagramas M, Q y N.
14) Verificación de equilibrio global de la estructura ΣFx = 0 ; ΣFy = 0 ; ΣMi = 0.
Pasos del método de deformaciones:
3

4. Es a NUDO FIJO porque no está aplicada una fuerza colineal a algún eje de barra
que no la respalde un apoyo.
Por lo tanto, no hay forma de desplazar al nudo en el sentido horizontal y vertical.
1 - ¿Como es una estructura a nudo fijo y desplazable?
4

5. Es a NUDO DESPLAZABLE cuando una barra por causa de una fuerza exterior se desplaza.
Por lo tanto, se puede desplazar al nudo en el sentido horizontal o vertical dependiendo de cómo este
la barra y como este aplicada la F.
Si sobre ese eje hay aplicada una fuerza exterior tanto puntual como distribuida uniforme o triangular.
Por consecuencia cuando un NUDO se desplaza las barras que intersecan con ese nudo giran.
5

6. 6
Es a NUDO FIJO porque es
simétrica.
Es a NUDO DESPLAZABLE
porque aunque se le aplica
una fuerza puntual vertical en
el medio, el apoyo cambia
por ende deja de ser una
estructura simétrica.

7. 7
Es a NUDO FIJO porque al ser
barras diagonales, si bien hay
una pequeño giro en los giros,
no se desplazan.
Es a NUDO DESPLAZABLE
porque la viga no tiene
ninguna restricción al
desplazamiento en x-x.

8. 8
Es a NUDO DESPLAZABLE
porque la viga no tiene
ninguna restricción al
desplazamiento en x-x.
Y la fuerza puntual sobre la
primer columna, produce una
acción en la viga.
Es a NUDO DESPLAZABLE
porque la viga no tiene
ninguna restricción al
desplazamiento en x-x.
Y la fuerza puntual sobre el
voladizo, produce un
momento en la columna, que
a su vez este produce una
acción en la viga.

9. 9

10. 10
Es a NUDO DESPLAZABLE porque la viga no tiene ninguna restricción al desplazamiento en x-x.
Y la fuerza distribuida uniforme vertical sobre la viga, produce un descenso y a su vez el
desplazamiento en X de la viga.

11. 2- Como me doy cuenta de como cortar la estructura y si mirar
para un lado, para el otro o ambos?
11
Básicamente, corto a un lado u
otro del nivel que se desplaza, o a
ambos lados. Depende del
conocimiento de las proyecciones
de las fuerzas.
Y miro hacia un lado o al otro o
ambos, si tengo incógnitas de
vínculos es decir, apoyos.

12. K3
K3
K3
K2
K3
K3
K3
K2
1 2
3 4
5
1 2
3 4 5
L23 = 3 m
L34 = 3 m
L12 = 3 m
3- Como giran los nudos y barras?
12

13. 4- Determino Kab según el tipo de barra que sea?
13
K2
K3
K3 K3
Detalle Nudo 2
Detalle Nudo 4
Detalle Nudo 2
Detalle Nudo 4
K3
K2
K3 K3
• K3: Empotramiento perfecto o empotramiento elástico (dos o más barras que concurren). Debe restringir
(X;Y;M).
• K2: Nudos articulados, apoyos móviles o apoyo fijo en el extremo. Debe restringir (X;Y).

14. 14

15. K2
K3
K3 K3
K3
K2
K3 K3
K’3-4
K2-3
K1-2
K1-2
K2-3
K’3-4
15

16. 5- Ecuación de nudo fijo
16

17. Ecuación de nudo desplazable
17

18. 18
Ecuación de nudo desplazable
�.

19. 6- Ecuación de desplazamiento
19
Plantean el equilibrio de las fuerzas que actúan en las secciones de los elementos
estructurales afectados por un corte.

20. Ecuación de nudo desplazable
20
�.
NOTA: En la suma algebraica se debe interpretar el signo de cada M.

21. 21

22. Las Ph representan a las acciones externas colineales a la barra de desplazamiento y las
Acc Q representan las acciones en el extremo que coincide con la barra de desplazamiento
(es igual a las reacciones en ese extremo pero cambiándole de signo).
Saco de la tabla 4 como si fueran bi-articulada las reacciones y luego le cambio el signo
para obtener “Acc Q”.
22

23. 23
Y se le debe cambiar el sentido por
que en la tabla 4 son reacciones.

24. 24
Para no confundirse
con la nomenclatura
genérica en el giro de
nudo a y b, tomen “b”
como el giro incógnita.
El Me 35, no va
porque el voladizo
no tiene rigidez,
solo se Toma AQ
en el nudo 3.
Convención + porque
esta a favor de gravedad

25. 25

26. 26

27. 27

28. 28
8 – Verificación de equilibrio de fuerzas horizontales a nivel:
7- Determino φ y ψ

29. 9 – Diagramas de esfuerzos:
29

30. 30

31. Verificaciones:
Σ Fx = 0
Σ Fy = 0
Σ M = 0
31

32. 32

33. 33