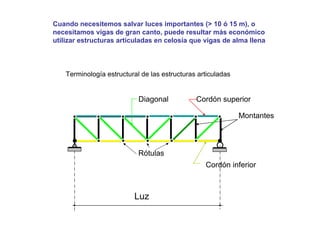
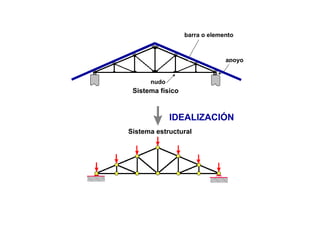
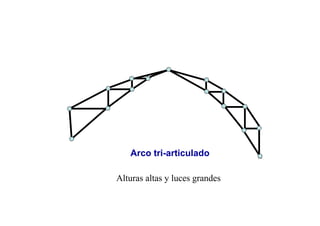
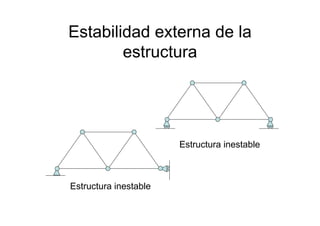
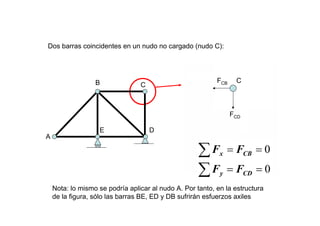
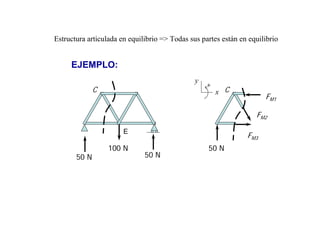
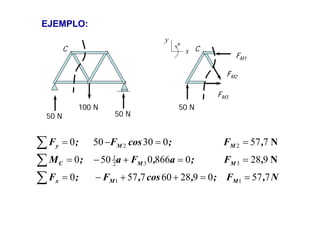
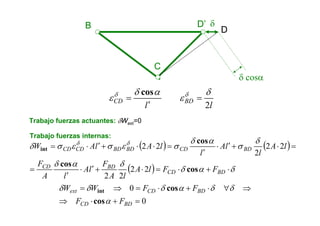
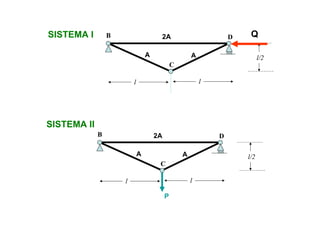
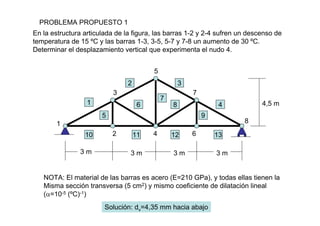
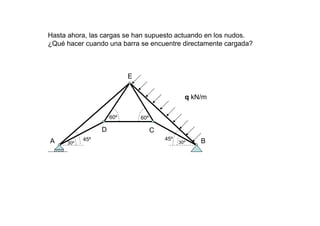
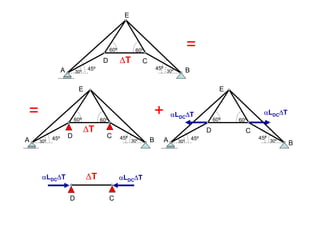
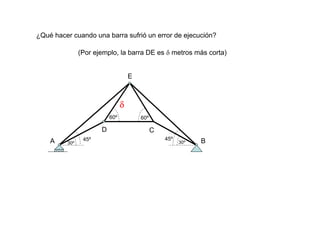
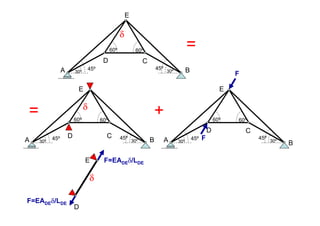
Las estructuras articuladas son útiles para salvar grandes luces y cuando se requieren vigas de gran canto de forma económica. Están formadas por barras unidas por rótulas que permiten movimiento en una dirección. Se pueden analizar estáticamente mediante el equilibrio de nudos o métodos gráficos como Cremona.

1. ESTRUCTURAS ARTICULADAS

2. Cuando necesitemos salvar luces importantes (> 10 ó 15 m), o
necesitamos vigas de gran canto, puede resultar más económico
utilizar estructuras articuladas en celosía que vigas de alma llena
Luz
Diagonal
Montantes
Cordón superior
Cordón inferior
Rótulas
Terminología estructural de las estructuras articuladas

3. Sistema físico
nudo
apoyo
barra o elemento
Sistema estructural
IDEALIZACIÓN

4. ANALÍSIS DE ESTRUCTURAS ARTICULADAS
ESTÁTICAMENTE DETERMINADAS

5. Luces cortas (<20 m)
Plantas en las que se requiere espacio vertical

6. Luces moderadas (20-30 m)
Su diseño puede modificarse para conseguir techos planos
Howe Pratt

7. Luces grandes (>30 m)
Fan Fink

8. Aplicable cuando se desean cubiertas planas
Warren

9. Cuando la localización de pilares no es problema
Cuando se precisa iluminación natural
En diente de sierra
techo techo
ventana ventana

10. Garajes y hangares aeronáuticos

11. Alturas altas y luces grandes
Arco tri-articulado

12. Hipótesis de diseño
• Las barras se unen unas a otras mediante uniones flexibles
– Los ejes de las barras son concurrentes en un punto
– En la realidad, esta unión proporciona alguna rigidez (tensiones
secundarias)

13. Formadas por triángulos
ESTRUCTURAS ARTICULADAS CANÓNICAS

14. ESTRUCTURAS ARTICULADAS COMPUESTAS
Cerchas simples
Cerchas
simples

15. ESTRUCTURAS ARTICULADAS ISOSTÁTICAS O ESTRICTAMENTE COMPLETAS
Son aquéllas en las que pueden determinarse los esfuerzos axiles en todas las barras utilizando,
exclusivamente, las ecuaciones de la estática. Si denominamos b al número de barras de la
Estructura, n al número de nudos de la misma y c al número de coacciones externas, podemos
establecer:
Número de incógnitas por barra: 4
Número de incógnitas: 4b + Coacciones externas: c = 4b+c
Número de ecuaciones que podemos plantear:
Equilibrio de una barra: 3 (ΣH=0, ΣV=0 y ΣM=0)
Equilibrio de un nudo: 2 (ΣH=0 y ΣV=0)
3b+2n
El problema es
estáticamente
determinado
cuando:
4b+c=3b+2n
b=2n-c
GDH=b+c-2n
Sí GDH < 0 (Mecanismo)
Sí GDH = 0 (Isostática ?)
Sí GDH >0 (Hiperestática)

16. La condición anterior de isostaticidad es una condición necesaria, pero no suficiente:
b=9, n=6, c=3 ¡Se cumple la condición! b=9, n=6, c=3
¡Se cumple también la condición
pero no existe equilibrio, ante
las posibles cargas, por tratarse
de un mecanismo!
Pero, desde luego

18. Estabilidad externa de la
estructura
Estructura inestable
Estructura inestable

19. Métodos de análisis
• Método de los nudos
• Método de las
secciones
• Métodos gráficos
(Cremona)

20. Métodos de análisis
• Método de los nudos
• Método de las
secciones
• Métodos gráficos
(Cremona)

21. Estructura articulada en equilibrio => Todos y cada uno de sus nudos están en equilibrio
500 N
2 m
2 m
A
B
C
FAB (tracción)
500 N
F (compresión)
B

22. Procedimiento
• Plantee las ecuaciones de equilibrio en cada nudo
• Tenga en cuenta las posibles simetrías
• Identifique las barras que no sufren ningún esfuerzo
– (i) cuando sólo dos barras de diferentes direcciones coincidan en
un nudo, y éste no está exteriormente cargado, ninguna de las dos
barras sufre esfuerzo axil
– (ii) Si tres barras coinciden en un nudo, y éste no está cargado, y
dos de las barras tienen la misma dirección, la barra no colineal
con las dos anteriores no sufre esfuerzo axil

23. Dos barras coincidentes en un nudo no cargado (nudo C):
∑
∑
==
==
0
0
CDy
CBx
FF
FF
Nota: lo mismo se podría aplicar al nudo A. Por tanto, en la estructura
de la figura, sólo las barras BE, ED y DB sufrirán esfuerzos axiles
A
B C
DE
CFCB
FCD

24. Tres barras coincidentes en un nudo no cargado (nudo D) siendo dos de ellas
colineales:
∑
∑
==
⇒=
0
0
DFy
DEDCx
FF
contrariasyigualesFyFF
D
E
C
F
xy
D
FDC
FDE
FDF

25. Métodos de análisis
• Método de los nudos
• Método de las
secciones
• Métodos gráficos
(Cremona)

26. Estructura articulada en equilibrio => Todas sus partes están en equilibrio
100 N
50 N50 N
C x
y
+
50 N
FM1
FM2
FM3
C
EJEMPLO:
E

27. Ecuaciones de equilibrio
Si tomamos momentos respecto de C podríamos determinar
el valor de FM3.
Si, posteriormente, tomamos momentos respecto de E,
determinaríamos FM1, …..
∑
∑
∑
=
=
=
0
0
0
M
F
F
y
x

28. 100 N
50 N50 N
N,F;,cos,F;F
,F;a,Fa;M
,F;cosF;F
MMx
MMC
MMy
7570928607570
92808660500
757030500
11
332
1
22
==++−=
==+−=
==−=
∑
∑
∑
N
N
C x
y
+
50 N
FM1
FM2
FM3
C
EJEMPLO:

29. Métodos de análisis
• Método de los nudos
• Método de las
secciones
• Métodos gráficos
(Cremona)

30. CÁLCULO DE DESPLAZAMIENTOS
Para calcular desplazamientos en nudos de una estructura articulada, aplicaremos
el teorema de Castigliano. Para ello, consideraremos como Sistema 0 el sistema
estructural real, con sus cargas, del que partimos, y como Sistema I el mismo sistema
estructural pero, ahora, sólo sometido a una carga unidad en el nudo y dirección en
que deseamos obtener el desplazamiento.
Sin embargo, puede haber casos en los que, además de cargas mecánicas, algunas
barras experimenten un cambio de temperatura o que, alguna de ellas, presente un
error de fabricación (que haya quedado más corta o más larga que la longitud
requerida).
En estas condiciones, la energía elástica del sistema estructural se expresa como:
∑∑∑
∆
∆
∂+∂+
Ω⋅
⋅
=
Tcon
barras
T
ii
errorcon
barras
e
ii
i
ii
barras
NN
E
LN
U
2
2
1
e
i∂
T
i
∆
∂
= error de ejecución de la barra i
= cambio de longitud de la barra i debido a la variación de temperatura
ii
T
i TL ∆=∂∆
α

31. ∑∑∑ ∆
∂+∂+
Ω
=
∂
∂
= T
i
I
i
e
i
I
i
barras i
iI
ii
j
j NN
E
L
NN
P
U
d 0
Al igual que hicimos para el caso de cargas mecánicas actuando sobre la estructura,
el desplazamiento de un nudo en una determinada dirección lo calcularemos como
ya hacíamos sólo que, ahora, hay que añadir los sumandos:
∑ ∂e
i
I
iN
∑ ∆
∂ T
i
I
iN

32. ( )dVol
dfdVolf
V
yzyzxzxzxyxyzzyyxx
V
V
∫∫∫
∫∫∫ ∫∫
+++++=
=Ω⋅+⋅
Ω
Ω
δδδδδδ
γτγτγτεσεσεσ
δδ
rrrr
0=Ω⋅+⋅∫∫∫ ∫∫Ω
Ω dfdVolf
V
V δδ
rrrr
( )
( ) ( )DB
DB
DBCB
CB
CB
V
yzyzxzxzxyxyzzyyxx
LA
L
LA
L
dVol
⋅+⋅=
=+++++∫∫∫
βδ
σ
αδ
σ
γτγτγτεσεσεσ δδδδδδ
coscos
( ) ( ) 0=⋅+⋅ DB
DB
DBCB
CB
CB LA
L
LA
L
βδ
σ
αδ
σ
coscos
T.T.V.
Trabajo virtual
fuerzas exteriores:
Trabajo
virtual
tensiones
internas:

33. En el sistema articulado de la figura formado por tres barras de
idéntico material y siendo las áreas de sus respectivas
secciones transversales: A, para las barras BC y CD, y 2A para
la barra BD, determinar, cuando, sobre él actúa la carga P:
a.- Las fuerzas axiles a las que se encuentran sometidas cada
una de las barras
b.- La energía elástica que almacena el sistema
c.- El desplazamiento vertical del nudo C y el horizontal del
nudo D.
2A
A A
P
l l
l/2
B
C
D

34. ASPECTOS GEOMÉTRICOS DE LA ESTRUCTURA ARTICULADA
l,
cos
l
CDBC
,
l
/l
arctan
1181
56526
2
===
==
α
α
2A
A A
P
l l
l/2
B
C
D
α α

35. NUDO B NUDO C
FBC=FCD por simetría
RESOLUCIÓN DE LA EXTRUCTURA POR EQUILIBRIO DE NUDOS:
PcosP,F
FP,F
PsenF
BD
BCCD
CD
==
==
=
α
α
1181
1181
2
FBC=1,118P
FBD
RB
P
FBC FCD
α α

36. B D’
C
δ
RESOLUCIÓN DE LA EXTRUCTURA POR EL P.T.V.:
Desplazamientos virtuales:
B y C no se desplazan
D lo hace hacia su izquierda
una magnitud δ
2A
A A
P
l l
l/2
B
C
D
α α

37. B D’
C
δ
D
δ cosα
ll
BDCD
2
δ
ε
αδ
ε δδ
=
′
=
cos
( ) ( )
( ) δαδ
δαδ
δ
σ
αδ
σεσεσδ δδ
⋅+⋅=⋅+′⋅
′
=
=⋅+′⋅
′
=⋅⋅+′⋅=
BDCD
BDCD
BDCDBDBDCDCD
FFlA
lA
F
lA
lA
F
lA
l
lA
l
lAlAW
cos
cos
cos
int
22
22
22
2
22
Trabajo fuerzas actuantes: δWext=0
Trabajo fuerzas internas:
0
0
=+⋅⇒
⇒∀⋅+⋅=⇒=
BDCD
BDCDext
FF
FFWW
α
δδαδδδ
cos
cosint

38. AE
Pl
d
AE
lP
Pd
79638981
2
1 2
,,
=⇒=
WU =
NUDO C:
NUDO D:
( ) ( )
EA
lP
EA
lP
E
A
P
lu BD
⋅
=
⋅
==⋅=
2
222ε
w
( )
( ) ( )
∑ =+
⋅
=++==
AE
lP,
AE
l,P,
EA
lP
UUU
EA
LF
U CDBCBD
i
ii
2222
8981
2
11811181
2
22
2
2

39. PRIMER TEOREMA DE CASTIGLIANO:
AE
Pl
AE
Pl
P
U
d
796328981 ,,
=
⋅
=
∂
∂
=

40. Q
Determinar, aplicando el teorema de reciprocidad y para la
estructura articulada del problema anterior el desplazamiento
vertical del punto C cuando actúa la carga Q que se observa
en la figura:
2A
A A
l l
l/2
B
C
D

41. SISTEMA I
SISTEMA II
Q2A
A A
l l
l/2
B
C
D
2A
A A
P
l l
l/2
B
C
D

42. ( ) ( )←⋅=↓⋅ II
D
I
C uQdP
EA
lP
uII
D
⋅
=
w
( ) ( )
EA
lQ
u
P
Q
d II
D
I
C
⋅
=←⋅=↓

43. 1
2
3
4
5
6
8
7
1
2 3
4
5
6
7
8
9
10 11 12 13
3 m 3 m 3 m 3 m
4,5 m
En la estructura articulada de la figura, las barras 1-2 y 2-4 sufren un descenso de
temperatura de 15 ºC y las barras 1-3, 3-5, 5-7 y 7-8 un aumento de 30 ºC.
Determinar el desplazamiento vertical que experimenta el nudo 4.
NOTA: El material de las barras es acero (E=210 GPa), y todas ellas tienen la
Misma sección transversa (5 cm2) y mismo coeficiente de dilatación lineal
(α=10-5 (ºC)-1)
PROBLEMA PROPUESTO 1
Solución: dv=4,35 mm hacia abajo

44. Determinar los desplazamientos horizontal y vertical del nudo E de la estructura
articulada de la figura.
Tómese EA=100 MN
A
E
D C
B
20 m
45º
30º
60º 60º
45º
30º
Solución:
dh=8,15 mm
dv=8,67 mm
10 kN
PROBLEMA PROPUESTO 2

45. Hasta ahora, las cargas se han supuesto actuando en los nudos.
¿Qué hacer cuando una barra se encuentre directamente cargada?
A
E
D C
B45º
30º
60º 60º
45º
30º
q kN/m

46. A
E
D C
B45º
30º
60º 60º
45º 30º
q kN/m
A
E
D C
B
45º
30º
60º 60º
45º 30ºA
E
D C
B45º
30º
60º 60º
45º 30º
q kN/m
+
=
RE
RB
=
E
q kN/m
RE
RB

47. ¿Qué hacer cuando una barra se encuentra sometida a un incremento térmico?
A
E
D C
B45º
30º
60º 60º
45º
30º
∆T
(Por ejemplo, la barra DC sufre un incremento térmico ∆T)

48. A
E
D C
B45º
30º
60º 60º
45º 30º
A
E
D C
B
45º
30º
60º 60º
45º 30ºA
E
D C
B45º
30º
60º 60º
45º 30º
+
=
=
∆T
D C
∆T
∆T αLDC∆TαLDC∆T
αLDC∆T αLDC∆T

49. ¿Qué hacer cuando una barra sufrió un error de ejecución?
A
E
D C
B45º
30º
60º 60º
45º
30º
δ
(Por ejemplo, la barra DE es δ metros más corta)

50. A
E
D C
B45º
30º
60º 60º
45º 30º
A
E
D C
B
45º
30º
60º 60º
45º 30ºA
E
D C
B45º
30º
60º 60º
45º 30º
+
=
=
δ
δ
E
D
δ
F=EADEδ/LDE
F=EADEδ/LDE
F
F

51. ESTRUCTURAS ARTICULADAS
ESTÁTICAMENTE INDETERMINADAS

52. 2 m
2 m
5 kN1 2
3
4
GDLE=3
CE=3
GHE=0
(estructura externamente isostática)
GDLI=3n-3=3.6-3=15
CI=2(nnudo -1)=2(3-1).4=16
GHI=1
(estructura internamente hiperestática)

53. 5 kN1 2
3
4
N13
N13
N13
N13
1
3
Sistema 0
(isostático)
Sistema 2
Desplazamiento relativo entre los nudos 1 y 3 del sistema 0=
= Desplazamiento entre esos mismos nudos del sistema 2
(los desplazamientos mencionados deben entenderse medidos en la dirección 1-3)

54. 5 kN1 2
3
4
N13
N13
Sistema 1
(isostático)
RESOLUCIÓN DEL SISTEMA 0
Barra Axil
1-2 -N13/
2-3 5-N13/
3-4 5-N13/
4-1 -N13/
2-4 -5 +N13
2
2
2
2
2

55. 1 2
3
4
1
1
Sistema 1
(isostático)
RESOLUCIÓN DEL SISTEMA 1 (Auxiliar para aplicar Castigliano)
Barra Axil
1-2 -1/
2-3 -1/
3-4 -1/
4-1 -1/
2-4 1
2
2
2
2

56. Barra Axil
1-2 -N13/
2-3 5-N13/
3-4 5-N13/
4-1 -N13/
2-4 -5 +N13
2
2
2
2
2
Barra Axil
1-2 -1/
2-3 -1/
3-4 -1/
4-1 -1/
2-4 1
2
2
2
2
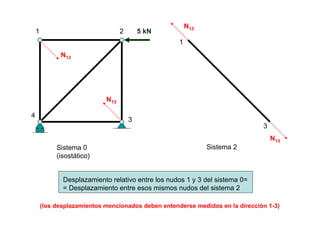
Estado 0 Estado 1
])(-))(([
EA
1
nto)(acercamie 2225122
2
522
22
11
13
131300
13 ⋅+⋅+⋅⋅−+⋅⋅−−==∆ ∑ N
NN
LNN
EA barras
i
I
ii
)]()([N
EA
1
nto)(acercamie 13 22102240
13 +−+=∆

57. RESOLUCIÓN DEL SISTEMA 2
N13
N13
1
3
Sistema 2
EA
N
to)(alejamien 13 222
13 =∆

58. to)(alejamiennto)(acercamie 2
13
0
13 ∆−=∆
EA
N
-)]()([N
EA
1 13
13
22
2210224 =+−+
N13=3,53 kN