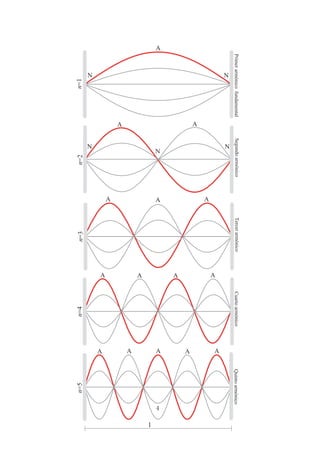
Este documento describe un experimento de laboratorio para estudiar ondas estacionarias en una cuerda elástica. El objetivo es comprender el concepto de onda estacionaria y determinar la velocidad de propagación midiendo las frecuencias de resonancia para diferentes longitudes de la cuerda. Se espera obtener tablas con los valores de frecuencia frente al orden armónico, y gráficas de las cuales se pueden calcular las velocidades de propagación y tensiones de la cuerda.

1. Practicas de laboratorio de Fsica I
Ondas estacionarias
Curso 2010/11
1 Objetivos
Comprender el concepto de onda estacionaria
Determinar la velocidad de propagacion de las ondas estacionarias en una cuerda
2 Material
Cuerda elastica Transformador de voltaje Generador de frecuencias
Motor electrico Multmetro digital
3 Fundamento teorico
Las ondas con

2. nadas en una region del espacio (como las ondas en las cuerdas de una
guitarra, las ondas sonoras en el tubo de un organo o las ondas longitudinales en un muelle)
se re
ejan en los extremos y las ondas incidentes y re
ejadas coinciden en esa misma
region. Por el principio de superposicion dichas ondas se combinan sumandose. Para una
cuerda, muelle o tubo determinados existen ciertas frecuencias en que la combinacion da
como resultado lo que se denomina una onda estacionaria. En esta situacion los elementos
de la cuerda o muelle vibran alrededor de su posicion de equilibrio, pero la onda da la
sensacion de no desplazarse. Sus aplicaciones son importantes por ejemplo en el dise~no
de instrumentos musicales y en ramas de la ingeniera como la construccion de puentes y
edi

3. cios.
Si se

4. jan los extremos de una cuerda y se hace vibrar con determinadas frecuencias
se obtienen ondas estacionarias como las que se muestran en la