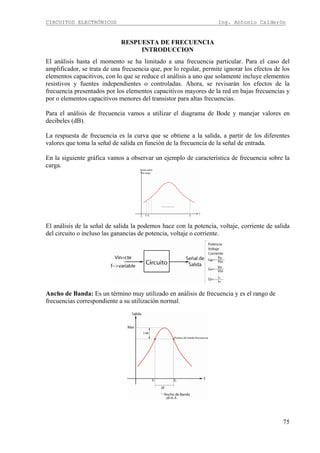
Este documento presenta el diseño de amplificadores con transistores bipolares. Comienza con una introducción al transistor bipolar y sus características. Luego describe tres configuraciones básicas del transistor y procede a explicar el diseño de amplificadores en emisor común, base común y colector común. Incluye ecuaciones para calcular la ganancia, impedancia de entrada y condiciones para evitar distorsiones en la señal de salida.






![CIRCUITOS ELECTRÓNICOS Ing. Antonio Calderón
9
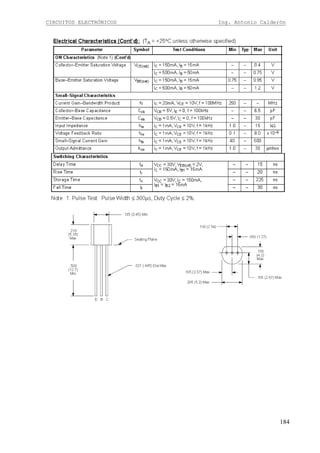
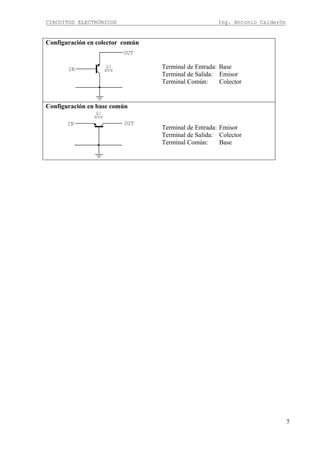
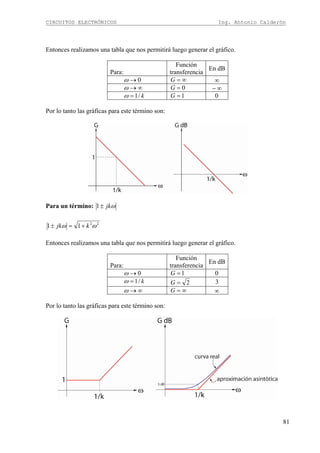
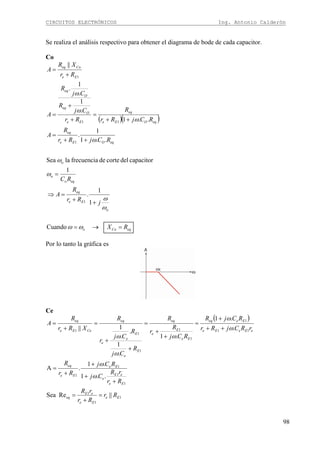
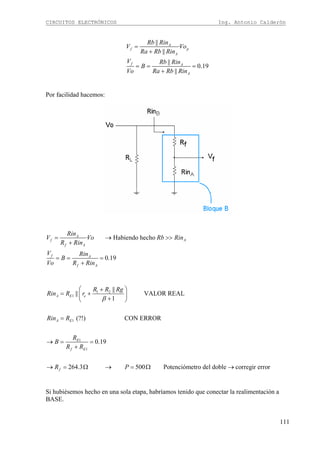
DISEÑO DE AMPLIFICADOR EN EMISOR COMÚN
Circuito
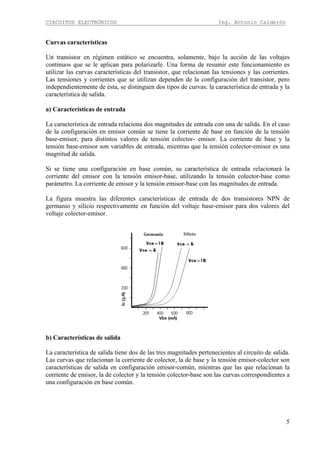
En el circuito amplificador en emisor común podemos observar que la señal ingresa por la
Terminal de base y la salida esta en e Terminal de colector. Además debemos mencionar que
la señal de salida esta desfasada 180º con respecto a la señal de entrada
La regla general para obtener la ganancia en un circuito de emisor común es: “Todo lo que
está en colector para señal divido para todo lo que está en emisor para señal”.
Por lo tanto se obtiene la expresión de ganancia del circuito mostrado inicialmente:
1
||
Ee
LC
Rr
RR
A
+
=
Dado que la señal ingresa en el Terminal de la base se obtiene la expresión de la impedancia
de entrada:
TRinRRRin |||| 21=
Donde RinT es la impedancia de entrada en el transistor y es igual a (β+1) por todo lo que esta
en emisor para señal, por lo tanto:
))(1( 1EeT RrRin ++= β
R1 y R2 están en paralelo puesto que para señal Vcc es tierra. A este paralelo le podemos
representar como RB.
Obteniendo la expresión final de la impedancia de entrada:
[ ]))(1(|| 1EeB RrRRin ++= β
Para el diseño de un circuito en emisor común es necesario tener muy en cuenta que se
cumpla la condición de impedancia de entrada por lo tanto:](https://image.slidesharecdn.com/64494485-calderon-circuitos-electronicos-130915171158-phpapp02/85/64494485-calderon-circuitos-electronicos-9-320.jpg)







![CIRCUITOS ELECTRÓNICOS Ing. Antonio Calderón
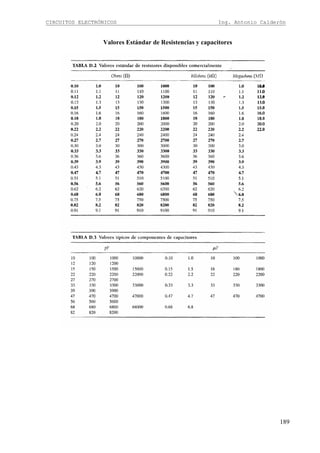
19
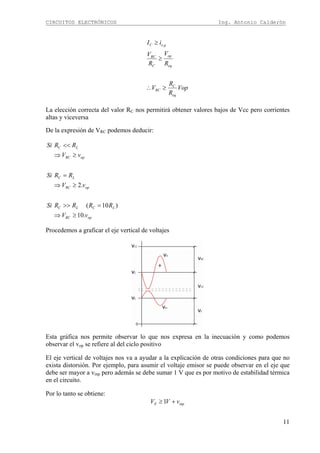
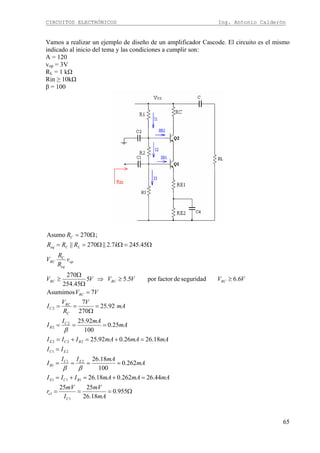
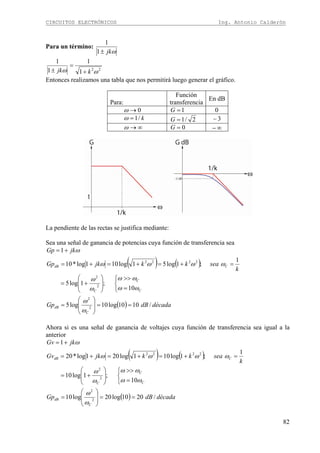
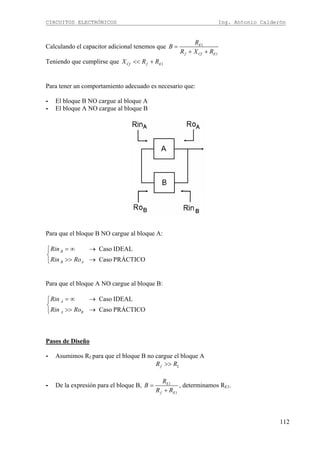
Ejercicio
En el siguiente circuito obtenga la ecuación de la ganancia e impedancia de entrada.
Recordemos la regla para obtener la ganancia “Todo lo que está en colector para señal divido
para todo lo que está en desde el punto de ingreso hacia emisor para señal”
Lo que esta en colector para señal: RC||RL
Lo que esta desde el punto de ingreso hacia emisor para señal: re+[(R1||R2)/(β+1)], el factor
1/(β+1) esta presente cuando se toma valores de la base vistos desde el emisor
Por lo tanto la ganancia es igual a:
1
||
||
21
+
+
=
β
RR
r
RR
A
e
LC
Para el caso de la impedancia de entrada observamos el circuito y obtenemos que:
⎟⎟
⎠
⎞
⎜⎜
⎝
⎛
+
+=
1
||
|| 21
β
RR
rRRin eE
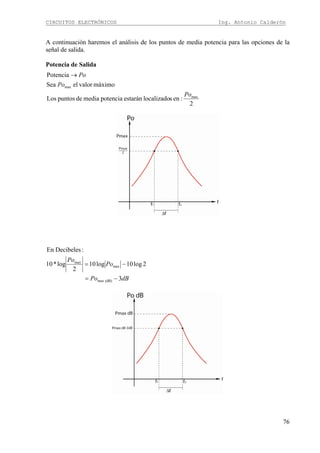
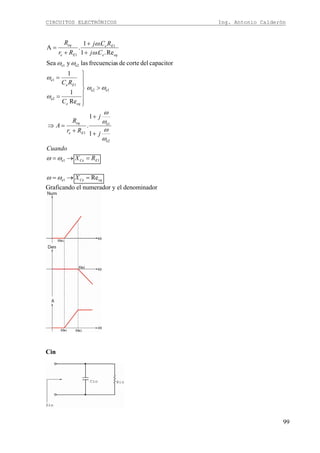
Condiciones de diseño
Siguiendo con el procedimiento de diseño para esta configuración, se inicia asumiendo la
resistencia RC y asumiendo el valor de VRC con la misma condición demostrada en el diseño
de emisor común para evitar distorsiones en la señal de salida.
LCeq
op
eq
C
RC
RRR
v
R
R
V
||siendo =
≥
La elección correcta del valor RC nos permitirá obtener valores bajos de Vcc pero corrientes
altas y viceversa](https://image.slidesharecdn.com/64494485-calderon-circuitos-electronicos-130915171158-phpapp02/85/64494485-calderon-circuitos-electronicos-19-320.jpg)




![CIRCUITOS ELECTRÓNICOS Ing. Antonio Calderón
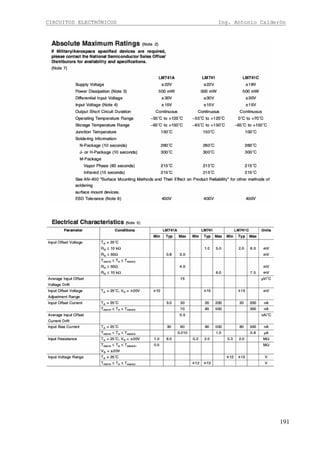
25
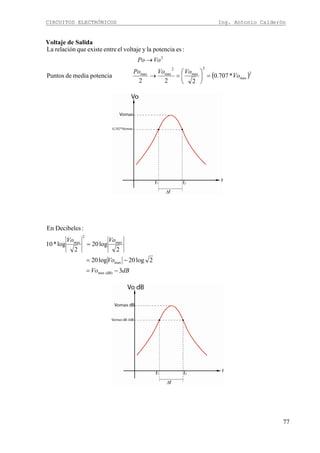
La fórmula de la ganancia entonces es:
LEEe
LE
RRRr
RR
A
||
||
21
2
++
=
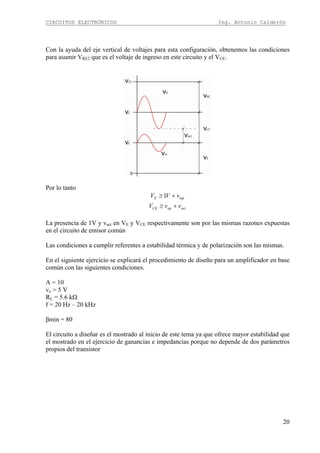
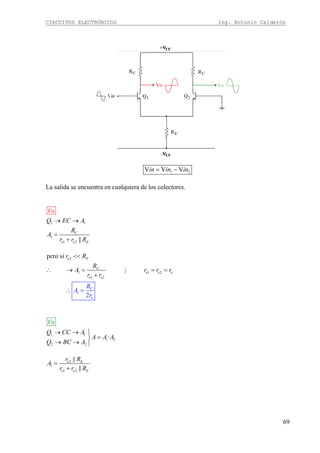
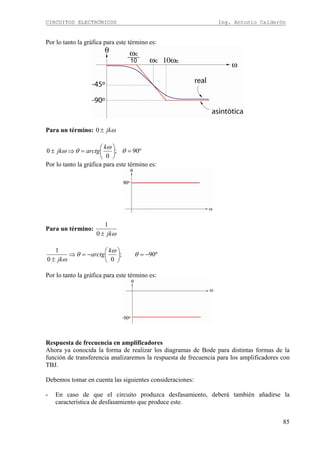
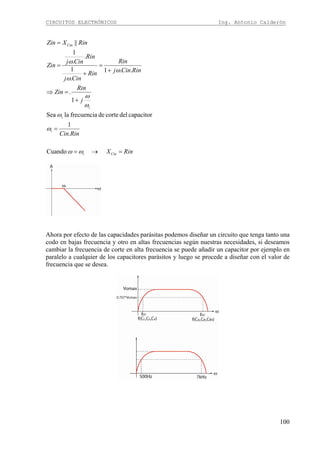
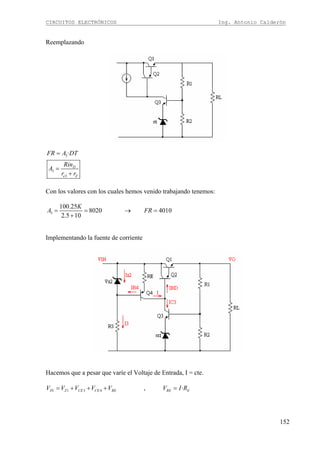
Continuando con el diseño en colector común. Dado que la señal ingresa por la base se
obtiene la expresión de la impedancia de entrada similar a la configuración en emisor común.
TRinRRRin |||| 21=
Donde RinT es la impedancia de entrada en el transistor y es igual a (β+1) por todo lo que esta
en emisor para señal, por lo tanto:
)||)(1( LEeT RRrRin ++= β
El paralelo entre R1 y R2 denominamos RB y el paralelo entre RE y RL denominamos Req
Obteniendo la expresión final de la impedancia de entrada:
[ ]))(1(|| eqeB RrRRin ++= β
Para el diseño de un circuito en colector común es necesario tener muy en cuenta que se
cumpla la condición de impedancia de entrada por lo tanto:
Analizando la expresión de la impedancia de entrada obtenemos que la peor condición para
que se cumpla esta es que RinT sea al menos Rin y reemplazando la ecuación de RinT
obtenemos](https://image.slidesharecdn.com/64494485-calderon-circuitos-electronicos-130915171158-phpapp02/85/64494485-calderon-circuitos-electronicos-25-320.jpg)









































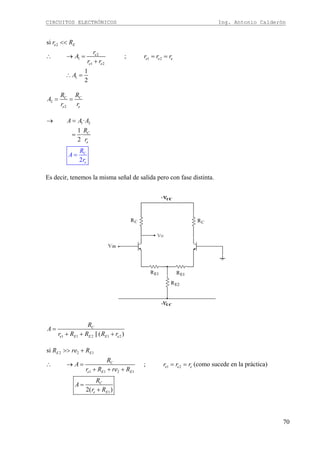



















































































![CIRCUITOS ELECTRÓNICOS Ing. Antonio Calderón
171
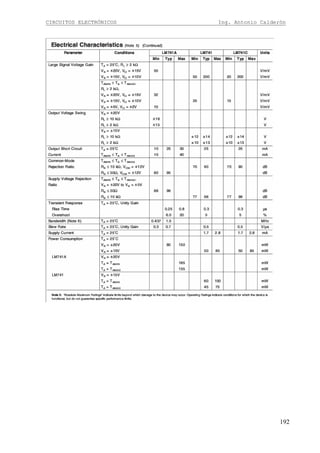
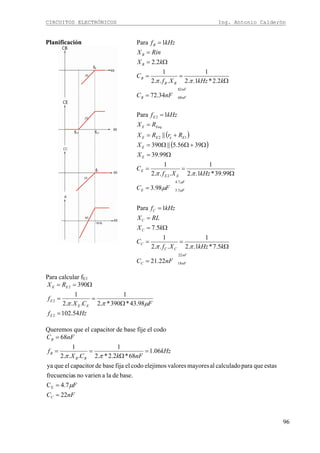
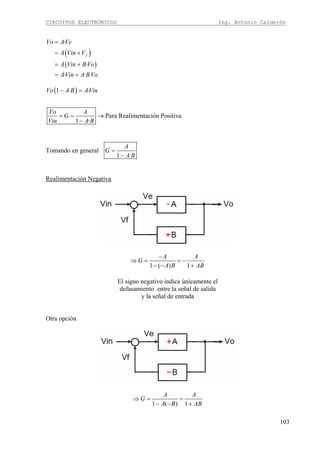
No se pone capacitor con RL porque se desperdicia potencia.
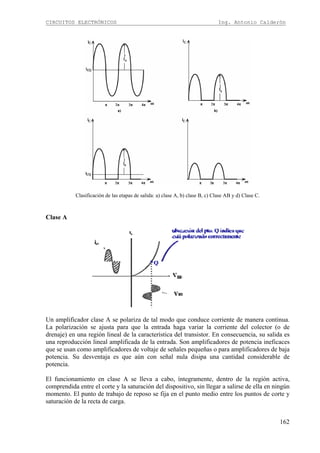
No se usa en la práctica.
Para 10 W de potencia de salida hay que elegir la curva de 20 W, y es mejor escoger una
superior para evitar posibles recortes.
En este caso las rectas de carga dinámica y estática son las mismas. El pto. Q es el eje de la
recta de carga dinámica.
2
·
1
· Potencia eficaz
2
·
·
CC CC CQ
pr
r CET CT
CEQ CQ
P V I
Vo
Po
Rac
Pd V I
V I
=
⎛ ⎞
= →⎜ ⎟
⎝ ⎠
=
=
100 [%] rendimiento
CC
Po
R
P
= × →](https://image.slidesharecdn.com/64494485-calderon-circuitos-electronicos-130915171158-phpapp02/85/64494485-calderon-circuitos-electronicos-171-320.jpg)