Este documento presenta conceptos básicos del álgebra binaria y sus aplicaciones en circuitos lógicos digitales. Introduce variables y operadores lógicos, funciones lógicas y tablas de verdad, propiedades del álgebra binaria como axiomas y teoremas, y grupos lógicos completos basados en compuertas NOR y NAND. El objetivo es proporcionar las bases teóricas para el estudio y diseño de circuitos lógicos digitales.

1. 1
Contenido
UNIDAD 2 – ÁLGEBRA BINARIA
Bibliografía
Martínez S. “Principios Digitales y Circuitos Lógicos”. Capítulo 7.
Editorial UNJu – 2º ed. Argentina. 2010.
Wakerly J.F. “DISEÑO DIGITAL. PRINCIPIOS Y PRÁCTICAS”.
Editorial Prentice Hall. Méjico. © 2001.
Tokheim R. L. “Principios Digitales”. Editorial Mc Graw Hill.
España. © 1990.
Técnicas y Estructuras Digitales - 2019
Profesores: Ing. Sergio L. Martínez - Ing. Víctor Sánchez R.
• Álgebra binaria.
• Elementos del álgebra binaria.
• Analogía eléctrica.
• Propiedades → Axiomas.
Teoremas.
• Funciones lógicas.
• Tablas de verdad.
• Funciones de una variable.
• Funciones de dos variables.
• Grupos lógicos completos.

2. U2 – ÁLGEBRA DE LOS CIRCUITOS DIGITALES
2
ÁLGEBRA BINARIA
Concepto
• La denominación de álgebra binaria se debe a que
toda su estructura se basa en un sistema de
numeración particular como es el sistema binario,
similarmente como ocurre con el álgebra decimal
respecto del sistema de numeración decimal.
• También se la conoce como álgebra de Boole o
álgebra booleana por estar fundamentada en los
estudios del matemático inglés George Boole.
• Otra denominación muy apropiada es la de álgebra
de conmutación, pues proporciona las bases
formales para el estudio y diseño de los circuitos
lógicos, los cuales operan estrictamente en la
conmutación de dos estados eléctricos.

3. U2 – ÁLGEBRA DE LOS CIRCUITOS DIGITALES
3
ÁLGEBRA BINARIA
Definición
Si un conjunto b donde se han definido las
operaciones binarias + y *, una operación ––
, y dos
elementos diferente de b identificados como 0 y 1;
entonces la séxtupla
{b , + , * , ––
, 0 , 1}
se puede denominar álgebra de Boole o álgebra bina-
ria si se cumplen los siguientes axiomas para tres
elementos A, B y C cualesquiera, pertenecientes a b :

4. U2 – ÁLGEBRA DE LOS CIRCUITOS DIGITALES
4
ELEMENTOS DEL ÁLGEBRA BINARIA
Variables lógicas
Una variable lógica representará uno de los dos
estados posibles y eventualmente no definidos, de la
proposición que simbolice (verdadero o falso), de un
determinado dispositivo (prendido o apagado) o en
general de cualquier situación biestable (si - no).
Las variables algebraicas representan números.
Las varia bles lógicas contienen un sólo bit
(1=verdadero, 0=falso) y representan estados de una
proposición. Por esta razón, estos valores, dentro de
las variables lógicas, no tienen sentido de cantidades,
es decir, no pueden ser restados o multiplicados
como los números en general.
Se simbolizan con cualquier carácter
A, B, C, x1, var, logic3, π, φ, …

5. U2 – ÁLGEBRA DE LOS CIRCUITOS DIGITALES
5
ELEMENTOS DEL ÁLGEBRA BINARIA
Operadores lógicos
También llamados conectivos lógicos, son los elementos que
determinan el tipo de relación que se establecerá entre las
variables y/o constantes que concatenen. Para el álgebra binaria
se definen básicamente tres:
NEGACIÓN (NOT, NO o complemento): Devuelve el valor comple-
mentario de la constante, variable, variables o función lógica que
involucre. Se representa con un suprarayado. Por ejemplo:
Si X = 0  = 1
PRODUCTO LÓGICO (AND, Y o disyunción): Aplicado a dos o más
variables, produce un resultado 0 (falso), cuando al menos una de
las variables que involucre sea 0 (falso). Se representa con un
punto, asterisco o yuxtaposición. Por ejemplo:
Si C = 0  A . B . C = 0
SUMA LÓGICA (OR, O ó conjunción): Aplicado a dos o más
variables, produce un resultado 1 (verdadero), cuando al menos
una de las variables que involucre sea 1 (verdadera). Se
representa con un [+]. Por ejemplo:
Si C = 1  A + B + C = 1
X

6. U2 – ÁLGEBRA DE LOS CIRCUITOS DIGITALES
6
ELEMENTOS DEL ÁLGEBRA BINARIA
Operadores lógicos combinados
Hay ciertas combinaciones entre los operadores
primarios o simples, de uso tan frecuente, que ha
dado lugar a la definición de otros operadores
que se denominan secundarios, combinados o
dobles y son:
NAND o NO-Y: Es la negación del producto lógico.
NOR o NO-O: Es la negación de la suma lógica.
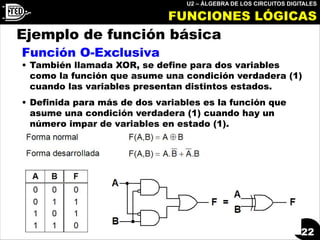
XOR: También denominado O-exclusiva, se representa
con el símbolo [].
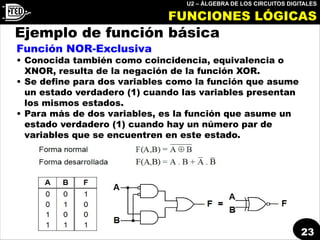
XNOR: También conocido como coincidencia,
comparación o equivalencia, se representa con
el símbolo [] o [].

7. U2 – ÁLGEBRA DE LOS CIRCUITOS DIGITALES
7
ELEMENTOS DEL ÁLGEBRA BINARIA
Compuertas lógicas
• El fundamento de la teoría lógica se basa en la
necesidad de estudiar y resolver las situaciones
que se plantean en forma simbólica o gráfica.
• Cada uno de los operadores tiene una representa-
ción gráfica llamadas compuertas lógicas.
• Permiten representar a las variables y los
operadores lógicos que las relacionan en forma
gráfica o circuital. Estas son

8. U2 – ÁLGEBRA DE LOS CIRCUITOS DIGITALES
8
ANALOGÍA ELÉCTRICA
Un 0 se representa con un contacto o interruptor abierto.
Un 1 se representa con un contacto o interruptor
cerrado.
La suma lógica se representa con contactos en paralelo y
el producto lógico se representa con contactos en serie.
La negación puede representarse como dos contactos
para cada variable, mecánicamente ligados, donde uno
está abierto y el otro cerrado.

9. U2 – ÁLGEBRA DE LOS CIRCUITOS DIGITALES
9
PROPIEDADES DEL ÁLGEBRA BINARIA
Axiomas
LEYES CONMUTATIVAS: El orden en que sean operadas las
variables no altera el resultado.
LEYES DISTRIBUTIVAS: La propiedad distributiva es válida
tanto del producto respecto de la suma, como de la
suma respecto del producto. Nótese que la segunda de
estas propiedades no es válida en el álgebra decimal.

10. U2 – ÁLGEBRA DE LOS CIRCUITOS DIGITALES
10
Axiomas
LEYES ASOCIATIVAS
LEYES DE TAUTOLOGÍA: Toda variable o función lógica
operada mediante la suma o producto lógico con su ele-
mento neutro, produce la misma variable o función
lógica. Para la suma lógica el elemento neutro es cero.
Para el producto lógico el elemento neutro es uno.
PROPIEDADES DEL ÁLGEBRA BINARIA

11. U2 – ÁLGEBRA DE LOS CIRCUITOS DIGITALES
11
Axiomas
LEYES DEL COMPLEMENTO: Toda variable o función operada,
a través de la suma o producto lógico, con la negación de sí
misma, produce el complemento de su elemento neutro
LEYES DE IDEMPOTENCIA: Toda variable o función operada
por si misma, a través de la suma o producto lógico, da
como resultado la misma variable o función.
PROPIEDADES DEL ÁLGEBRA BINARIA

12. U2 – ÁLGEBRA DE LOS CIRCUITOS DIGITALES
12
Axiomas
LEYES DE INVARIANZA: Toda variable o función operada con
su elemento neutro complementado produce ese mismo
elemento.
LEY DE INVOLUCIÓN: Toda variable o función lógica negada
dos veces da como resultado la misma variable o función.
Primer
corolario
Segundo
corolario
PROPIEDADES DEL ÁLGEBRA BINARIA

13. U2 – ÁLGEBRA DE LOS CIRCUITOS DIGITALES
13
Teoremas
LEY DE DUALIDAD: Todas las identidades que se establecen
para el álgebra binaria permanecen como tales si se
reemplazan ceros por unos y viceversa y suma por producto
lógico y viceversa (Como demostración de esta ley se
observan todas las leyes duales mostradas).
LEYES DE ABSORCIÓN
PROPIEDADES DEL ÁLGEBRA BINARIA

14. U2 – ÁLGEBRA DE LOS CIRCUITOS DIGITALES
14
Teoremas – Leyes de De Morgan
PROPIEDADES DEL ÁLGEBRA BINARIA

15. U2 – ÁLGEBRA DE LOS CIRCUITOS DIGITALES
15
Teoremas – Leyes de De Morgan
PROPIEDADES DEL ÁLGEBRA BINARIA

16. U2 – ÁLGEBRA DE LOS CIRCUITOS DIGITALES
16
Teoremas – Leyes de De Morgan
PROPIEDADES DEL ÁLGEBRA BINARIA

17. U2 – ÁLGEBRA DE LOS CIRCUITOS DIGITALES
17
FUNCIONES LÓGICAS
Definición
Es la relación que se establece entre una o más variables
lógicas (identificadas como independientes o de entrada),
mediante los operadores lógicos, cuyo resultado se
asigna a una nueva variable lógica (identificada como
dependiente o de salida).
F(A,B,C)=(A +B.C).C
Variable dependiente
Argumento
Variables independientes
Operadores

18. U2 – ÁLGEBRA DE LOS CIRCUITOS DIGITALES
18
Tabla de verdad
Es una organización tabular que contiene todas las posibles
combinaciones de valores que pueden establecerse entre
las variables de entrada y los correspondientes valores que
asume la o las variables de salida.
FUNCIONES LÓGICAS

19. U2 – ÁLGEBRA DE LOS CIRCUITOS DIGITALES
19
Tabla de verdad – Otros formatos
T.V. extendida: Contiene los resultados parciales de la función
para facilitar el cálculo.
T.V. horizontal: Ocupa menos espacio.
T.V. no gráfica: Se representa en forma numérica sin una
estructura gráfica. Útil en programación.
(XYZ,F) = (000,1) (001,1) (010,0) (011,0) (100,0) (101,0)
(110,1) (111,1)
FUNCIONES LÓGICAS

20. U2 – ÁLGEBRA DE LOS CIRCUITOS DIGITALES
20
Funciones básicas de una variable
F = f(A)
FUNCIONES LÓGICAS

21. U2 – ÁLGEBRA DE LOS CIRCUITOS DIGITALES
21
Funcionesbásicas
dedosvariables
F = f(A,B)
FUNCIONES LÓGICAS

22. U2 – ÁLGEBRA DE LOS CIRCUITOS DIGITALES
22
Ejemplo de función básica
Función O-Exclusiva
• También llamada XOR, se define para dos variables
como la función que asume una condición verdadera (1)
cuando las variables presentan distintos estados.
• Definida para más de dos variables es la función que
asume una condición verdadera (1) cuando hay un
número impar de variables en estado (1).
FUNCIONES LÓGICAS

23. U2 – ÁLGEBRA DE LOS CIRCUITOS DIGITALES
23
Ejemplo de función básica
Función NOR-Exclusiva
• Conocida también como coincidencia, equivalencia o
XNOR, resulta de la negación de la función XOR.
• Se define para dos variables como la función que asume
un estado verdadero (1) cuando las variables presentan
los mismos estados.
• Para más de dos variables, es la función que asume un
estado verdadero (1) cuando hay un número par de
variables que se encuentren en este estado.
FUNCIONES LÓGICAS

24. U2 – ÁLGEBRA DE LOS CIRCUITOS DIGITALES
24
GRUPOS LÓGICOS COMPLETOS
Definición y concepto
Un grupo lógico completo es el operador o conjunto de
operadores lógicos con los que se puede representar
cualquier función lógica.
• Básicamente se definen tres grupos lógicos completos
1. NOT – OR – AND (operadores primarios)
2. NOR (operador secundario)
3. NAND (operador secundario)
• Cualquier función lógica tienen formas equivalentes
utilizando los grupos 2 y 3 exclusivamente.
• Las compuertas basadas en los operadores NOR y NAND
también se las denominan compuertas universales.
• La utilidad principal es la construcción de circuitos
lógicos que emplean un mismo tipo de compuerta.
• Las funciones y circuitos que utilizan los grupos 2 y 3 son
más homogéneas pero suelen ser más extensas.

25. U2 – ÁLGEBRA DE LOS CIRCUITOS DIGITALES
25
Compuertas típicas (pinout)
séxtuple inversor
cuádruple 2-input OR
triple 3-input AND
cuádruple
2-input NOR
triple
3-input NOR
cuádruple 2-input NAND triple 3-input NAND doble 4-input NAND
GRUPOS LÓGICOS COMPLETOS

26. U2 – ÁLGEBRA DE LOS CIRCUITOS DIGITALES
26
Criterios de representación NOR / NAND
• Siempre que sea posible se debe trabajar con la función
minimizada.
• Desarrollar los operadores combinados (XOR / XNOR) a
sus representaciones NOT / OR / AND.
• La utilidad principal es la construcción de circuitos
lógicos que emplean un mismo tipo de compuerta.
• Aplicar las propiedades en forma conveniente (a toda o
parte de la función) para eliminar los operadores no
deseados.
• Para formatos con NOR debe buscarse la eliminación de
operadores AND y NAND.
• Para formatos con NAND debe buscarse la eliminación de
operadores OR y NOR.
GRUPOS LÓGICOS COMPLETOS

27. U2 – ÁLGEBRA DE LOS CIRCUITOS DIGITALES
27
Ejemplo de conversión NOR / NAND
Con NOR
• DeMorgan
• Involución
• De Morgan al producto lógico
Con NAND
• Involución al paréntesis
• De Morgan al paréntesis
• Involución inversa
• Involución a toda la función
F(A,B,C)=(A +B.C) . C
F(A,B,C)=(A +B+C) . C
F(A,B,C)=(A +B+C) . C
F(A,B,C)= A +B+C+C
A
B
C
F
F(A,B,C)=(A +B.C) . C
F(A,B,C)= A . B . C . C
F(A,B,C)= A . B . C . C
F(A,B,C)= A . B . C . C
A
B
C
F
GRUPOS LÓGICOS COMPLETOS

28. U2 – ÁLGEBRA DE LOS CIRCUITOS DIGITALES
28
GRUPOS LÓGICOS COMPLETOS
Ejemplo de conversión NOR / NAND
Con NOR Con NANDF(A,B,C)=(A +B.C) . C
F(A,B,C)= A +B+C+C
A
B
C
F
F(A,B,C)= A . B . C . C
A
B
C
F
B C
A
F
B
C
C
A+B+C
A+B+C + C
B
C
A
F
A
A.B.C
A.B.C . C
A.B.C . C
C