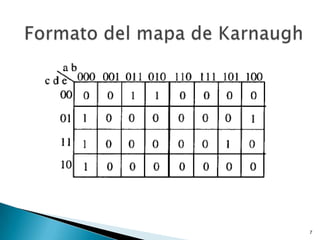
El documento describe el uso de mapas de Karnaugh para simplificar expresiones lógicas. Explica que los mapas de Karnaugh son un método gráfico para representar tablas de verdad que permite convertir una tabla en un circuito lógico de forma simple. También indica que los mapas solo son prácticos para problemas de hasta 5 variables debido a su crecimiento exponencial. El documento incluye ejemplos de cómo construir y simplificar expresiones usando mapas de Karnaugh.

1. Ing. Diego Avalos

2.  El algebra de Boole es útil para reducir
expresiones de funciones boleanas. Otro
método que podría resultar más conveniente
y fácil de visualizar para realizar estas
simplificaciones es la utilización de los mapas
de Karnaugh.
 Un mapa de Karnaugh es un método gráfico
que se utiliza para simplificar una ecuación
lógica para convertir una tabla de verdad a su
circuito lógico correspondiente en un proceso
simple y ordenado.
2

3.  Los mapas de Karnaugh tiene el mismo
problema de las tablas de verdad, aumenta su
tamaño en forma exponencial dependiendo
del número de variables de entrada.
 Los mapas de Karnaugh se pueden utilizar
para resolver problemas con cualquier
número de variables, sin embargo, debido al
crecimiento exponencial en su tamaño, sólo
son prácticos para problemas de hasta 5
variables. Para 6 variables o más es mejor
utilizar algebra de Boole.
3

4.  El mapa de Karnaugh es un medio gráfico
para representar una tabla de verdad, es
decir, es una relación entre las entradas de
un circuito y sus salidas.
A B X
0 0 1
x=A’B’+AB
0 1 0
1 0 0
1 1 1
4

5. A B C X x=A’B’C’+A’B’C+A’BC+ABC’
0 0 0 1
0 0 1 1
0 1 0 1
0 1 1 0
1 0 0 0
1 0 1 0
1 1 0 1
1 1 1 0
5

6. A B C D X
0 0 0 0 0 x=A’B’C’D+A’BC’D+ABC’D+ABCD
0 0 0 1 1
0 0 1 0 0
0 0 1 1 0
0 1 0 0 0
0 1 0 1 1
0 1 1 0 0
0 1 1 1 0
1 0 0 0 0
1 0 0 1 0
1 0 1 0 0
1 0 1 1 0
1 1 0 0 0
1 1 0 1 1
1 1 1 0 0
1 1 1 1 1
6

7. 7

8.  Los cuadros en el mapa se marcan de modo
que los cuadros adyacentes difieran sólo en
una variable tanto vertical como
horizontalmente (código gray).
 Una vez que se tiene el mapa, la expresión
lógica de la salida se puede obtener como
una suma de productos canónicos
considerando sólo las posiciones que tienen
1.
8

9. La expresión de salida obtenida se puede
simplificar combinando los cuadros del mapa
que contienen 1. Este proceso se denomina
agrupamiento.
Agrupamientos de dos términos (pares):
x=A’BC’+ABC’=BC’ x=A’BC’+A’BC=A’B
9

10. Agrupamientos de dos términos (pares):
x=A’B’C’+AB’C’
=B’C’
x=A’B’CD+A’B’CD’+AB’C’D’+ AB’CD’
=A’B’C+AB’D’
10

11. Agrupamientos de cuatro términos
(cuádruples):
x=C
x=AB
11

12. Agrupamientos de cuatro términos
(cuádruples):
x=BD x=AD’
12

13. Agrupamientos de cuatro términos
(cuádruples):
x=B’D’
13

14. Agrupamientos de ocho términos (octetos):
x=B’ x=D’
14

15. 1. Construir el mapa de Karnaugh.
2. Encontrar los unos que no sean adyacentes a
ningún otro uno (unos aislados).
3. Encontrar aquellos unos que sean adyacentes a
sólo otro uno (pares).
4. Agrupar los octetos aunque algunos unos se
hayan repetidos.
5. Agrupar cuádruples que contenga uno o más unos
que se hayan repetido. Utilizar el número mínimo
de agrupamientos.
6. Agrupar cualquier par que sea necesario para
incluir los unos que no se han repetido.
7. Realizar la suma de todos los agrupamientos
15

16. x=A’B’CD’+ACD+BD
16

17. x=A’B+BC’+A’CD
17

18. x=ABC’+A’C’D+A’BC+ACD
18

19. x=A’C’D+A’BC+AB’C’+ACD’
19

20.  Simplificar la expresión A’B’C’+B’C+A’B
utilizando mapas de Karnaugh
20

21.  Algunos circuitos lógicos se pueden diseñar
considerando que hay algunas condiciones de
entrada para las cuales no se especifica o no
afectan la salida. En este caso no se
especifica el valor de la variable y se puede
considerar como uno o como cero según
convenga en el procedimiento de reducción.
21

22. A B C X
0 0 0 1
0 0 1 1
0 1 0 1
0 1 1 0
1 0 0 0
1 0 1 0
1 1 0 1
1 1 1 0
22

23. Simplificar las expresiones dadas por:
1. f = a'b + ab' + ab
2. f = a'b + ab'c + c'
3. f = ac'd' + a'bd + abcd + ab'cd + a'bc'd' +
a'b'c'd‘ A B C X
4. 0 0 0 0
0 0 1 0
0 1 0 1
0 1 1 0
1 0 0 1
1 0 1 0
1 1 0 1
1 1 1 0
23

24. A B C X
5. 0 0 0 0
0 0 1 0
0 1 0 0
0 1 1 1
1 0 0 0
1 0 1 1
1 1 0 1
1 1 1 1
6. f=A’B’C’D’+A’BC’D’+AB’CD’+AB’CD’+AB’CD+
ABC’D
7. F=A’B’C’D+A’B’CD+A’BCD’+AB’C’D’+AB’C’D+
ABCD condiciones no importa: A’B’CD’, ABC’D
24

25.  Los mapas de Karnaugh presentan un
procedimiento ordenado para la
simplificación de expresiones lógicas
 Los mapas de Karnaugh pueden requerir
menos etapas en la reducción, especialmente
cuando la función contiene muchos términos.
 Con los mapas de Karnaugh siempre se
produce una expresión mínima y se reduce la
cantidad de errores.
25