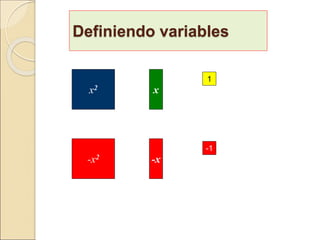
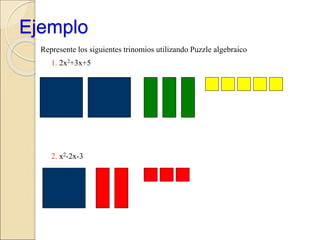
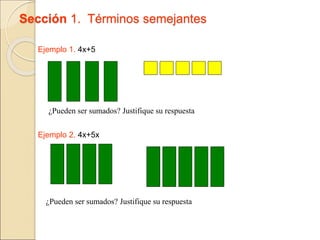
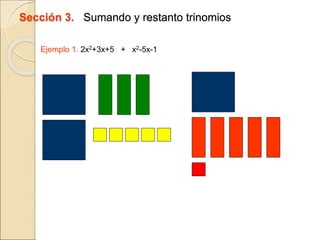
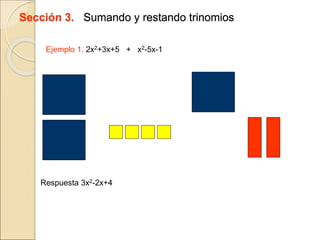
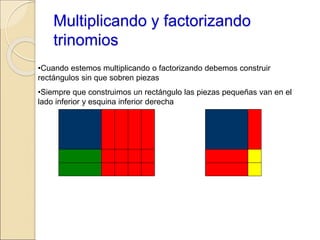
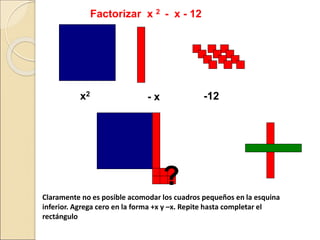
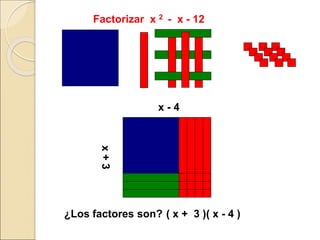
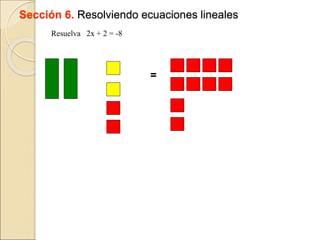
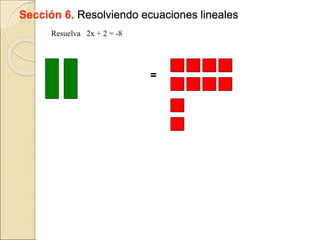
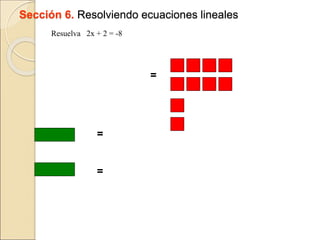
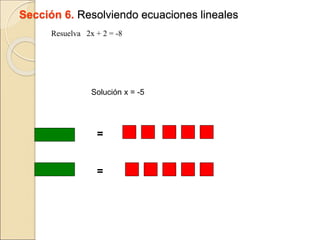
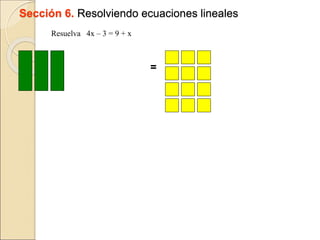
El documento describe cómo usar piezas de rompecabezas algebraicos (rectángulos de colores) para facilitar la comprensión de conceptos algebraicos en los estudiantes. Explica cómo los rectángulos de colores pueden usarse para representar variables, términos, sumar y restar expresiones, multiplicar trinomios, factorizar trinomios y resolver ecuaciones lineales.

1. USANDO PUZZLE ALGEBRAICO EN
MATEMÁTICA
Adaptado de: SOURCE: maths.slss.ie/resources/Algebra Tiles
Full Show.ppt
Presentado: KennethBaisden
JohnRoopchan
Traducido: LuisAlexander Fuentes

2. Puzzle Algebraico
Para trabajar con Puzzle algebraico es
necesario recordar que el color ROJO
significa negativo. Cualquier otro color
representa el signo mas.
+1 -1 = 0

3. ¿Qué es el Puzzle Algebraico?
Rectángulos de colores que
pueden ser utilizados para facilitar
en los estudiantes la comprensión
sobre el álgebra.

4. 1
Definiendo variables
x2
-x2
x
-x
-1

5. Ejemplo
Represente los siguientes trinomios utilizando Puzzle algebraico
1. 2x2+3x+5
2. x2-2x-3

6. Uso del Puzzle Algebraico
Puede ser usado (entre otros) para
Sección 1. Identificar terminos semejantes y no semejantes
Sección 2. Sumar y restar enteros
Sección 3. Simplificar expresiones
Sección 4. Multiplicar en álgebra
Sección 5. Factorizar trinomios
Sección 6. Resolver ecuaciones lineales

7. Sección 1. Términos semejantes
Ejemplo 1. 4x+5
¿Pueden ser sumados? Justifique su respuesta
Ejemplo 2. 4x+5x
¿Pueden ser sumados? Justifique su respuesta

8. Sección 2. Sumando y restando enteros
Ejemplo 1. 4-7
Ejemplo 2. –3-6

9. Sección 3. Sumando y restanto trinomios
Ejemplo 1. 2x2+3x+5 + x2-5x-1

10. Sección 3. Sumando y restando trinomios
Ejemplo 1. 2x2+3x+5 + x2-5x-1
Respuesta 3x2-2x+4

11. Sección 3. Sumando y restando trinomios
Ejemplo 2. 2x2+3x+2 - ( x2-2x+1 )
-
Una idea concreta para cambiar signos

12. Sección 3. Sumando y restando trinomios
Ejemplo 2. 2x2+3x+2 - ( x2-2x+1 )
Una idea concreta para cambiar signos

13. Ejemplo 2. 2x2+3x+2 - ( x2-2x+1 )
Una idea concreta para cambiar signo
Solución x2+5x+1
Sección 3. Sumando y restando trinomios

14. Práctica
Simplifique:
1) 6-7
2) 3-2-4-1
3) 5x2+2x
4) 2x2+4x+2x2-x
5) 3x2-2x+4+x2-x-2
6) x2-3x-2-x2-2x+4
7) 2x2-2x-1-3x2-2x-2
8) x2+2x+1- 3x2-x
9) x2-x+3-2x2+2x+x2-2x-5
Simplifique:
10)2-8-1
11)-5-1-4+1
12)x2+2
13)x2+5x+x2-2x
14)2x2-x+1 - (2x2-2x-5)
15)x2- 2x2-2x+4 - (x2+2x+3)
16)3x2-4x+2 - (x2+2)
17)x2+x-2 - 2(x2+2x-3)
18)-4x-3 - (2x2-2x-4)

15. Multiplicando y factorizando
trinomios
•Cuando estemos multiplicando o factorizando debemos construir
rectángulos sin que sobren piezas
•Siempre que construimos un rectángulo las piezas pequeñas van en el
lado inferior y esquina inferior derecha

16. Sección 4. Multiplicando en álgebra
Ejemplo 2. Multiplicar (x-1)(x-3)
Solución: x2-4x+3

17. Práctica
Multiplique lo siguiente:
1) x(x+3)
2) 2(x-5)
3) 3x(x-1)
4) (x+4)(x+3)
5) (x-1)(x+2)
6) (x-4)(x-2)
7) (3x-1)(x-3)
8) (x-1)(x-1)
9) (2x+1)2
10) (x-2)2

18. Factors and Area
- Una aproximación
geométrica
Una refuerzo de la
multiplicación
Sección 5. Factorizando trinomios

19. Represente (x+1)(x+3) acomodando las piezas en un
rectángulo
x
x 3
1
+
+
Reordenemos las piezas para mostrar la expresión:
x 2 + 4x + 3 How it works

20. x 2 + 6x + 8
Para factorizar la expresión formamos un rectángulo con
todas las piezas
x + 4
x
+
2
( x + 4 )( x + 2 )Los factores son
Factorizar x 2 + 6x + 8
Factorise x2+6x+8

21. x + 3
x
-
1
NOTA: LAS ROJAS SON NEGATIVAS
Ahora complete el rectángulo con los rectángulos negativos
Expresemos (x+3)(x-1) con un arreglo de piezas formando un
rectángulo
Reordenemos las piezas para mostrar la expresión
x2 + 3x -1x - 3 = x2 + 2x - 3
(x+3)(x-1)

22. Factorizar x 2 - 4x + 3
x2
- 4x + 3
x - 3
x - 1
Los factores son ( x - 3 )( x - 1 )

23. Factorizar x 2 - x - 12
x2
- x -12
Claramente no es posible acomodar los cuadros pequeños en la esquina
inferior. Agrega cero en la forma +x y –x. Repite hasta completar el
rectángulo
?

24. Factorizar x 2 - x - 12
¿Los factores son? ( x + 3 )( x - 4 )
x - 4
x+3

25. Sección 6. Resolviendo ecuaciones lineales
Resuelva 2x + 2 = -8
=

26. Sección 6. Resolviendo ecuaciones lineales
Resuelva 2x + 2 = -8
=

27. Sección 6. Resolviendo ecuaciones lineales
Resuelva 2x + 2 = -8
=
=
=

28. Sección 6. Resolviendo ecuaciones lineales
Resuelva 2x + 2 = -8
=
=
Solución x = -5

29. Sección 6. Resolviendo ecuaciones lineales
=
Resolver 4x – 3 = 9 + x
Puedes quitar figuras iguales de ambos lados
siempre que tengan el mismo color

30. Sección 6. Resolviendo ecuaciones lineales
=
Resuelva 4x – 3 = 9 + x
Puedes agregar la misma cantidad de figuras
iguales a ambos lados

31. Sección 6. Resolviendo ecuaciones lineales
=
Resuelva 4x – 3 = 9 + x

32. Sección 6. Resolviendo ecuaciones lineales
=
Resolver 4x – 3 = 9 + x
=
=

33. Sección 6. Resolviendo ecuaciones lineales
=
Resolver 4x – 3 = 9 + x
=
=
Solución x = 4

34. Práctica
Resuelva las siguientes
ecuaciones:
1) x+4 = 7
2) x-2 = 4
3) 3x-1 =11
4) 4x-2 = x-8
5) 5x+1 = 13-x
6) 2(x+3) = x-1
7) 2x-4 = 5x+8

35. Gracias