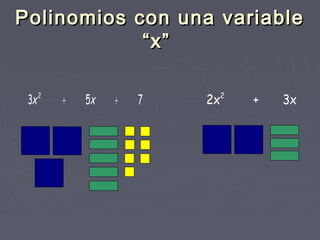
El documento describe el uso del ALGEPLANO para representar polinomios de segundo grado de dos variables y coeficientes enteros. El ALGEPLANO contiene piezas de plástico de diferentes formas, tamaños y colores que pueden representar términos y polinomios asignando variables a sus lados. Esto permite realizar operaciones algebraicas como adición, sustracción, multiplicación, división y factorización de una manera concreta y orientada al modelamiento matemático.

2. ALGEPLANOALGEPLANO
 Material utilizado para representarMaterial utilizado para representar
polinomios de segundo grado de coeficientespolinomios de segundo grado de coeficientes
enteros.enteros.
 Permite realizar las operaciones algebraicasPermite realizar las operaciones algebraicas
básicas:básicas:
AdiciónAdición
SustracciónSustracción
MultiplicaciónMultiplicación
DivisiónDivisión
FactorizaciónFactorización
 Parte de lo concreto y conlleva a lo abstractoParte de lo concreto y conlleva a lo abstracto

3. Modelamiento Matemático.Modelamiento Matemático.
► Orientado a la representación de
polinomios en el marco de los
monomios y polinomios de segundo
grado, de dos variables y de
coeficientes enteros.
METODOLOGÍA

4. Un juego de ALGEPLANO contiene un total de 70 piezas de plástico.
NombreNombre
PiezaPieza
Color y FormaColor y Forma
DimensiónDimensión CantidadCantidad
FichasFichas
CuadradoCuadrado
GrandeGrande
AzulAzul
4 cm. x 4 cm.4 cm. x 4 cm. 33
CuadradoCuadrado
GrandeGrande
RojoRojo
4 cm. x 4 cm.4 cm. x 4 cm. 33
RectánguloRectángulo
VerdeVerde
1 cm. x 4 cm.1 cm. x 4 cm. 88
RectánguloRectángulo
RojoRojo
1 cm. x 4 cm.1 cm. x 4 cm. 88
CuadradoCuadrado
PequeñoPequeño
AmarrilloAmarrillo
1 cm. x 1 cm.1 cm. x 1 cm. 2424
CuadradoCuadrado
PequeñoPequeño
RojoRojo
1 cm. x 1 cm.1 cm. x 1 cm. 2424
Se distinguen dos tipos de piezas según su forma (cuadrados y rectángulos) y
tres tipos según su tamaño (cuadrado grande, cuadrado pequeño y rectángulo).

5. Con ayuda del reconocimiento de las dimensiones de las fichas del
ALGEPLANO, asigna una variable a cada lado e identifica el concepto de
términos algebraicos y polinomios, representándolos física y simbólicamente.

6.  El Modelamiento de polinomios consiste en representar los términos
algebraicos de un polinomio partiendo de conceder un valor simbólico a las
piezas del “ALGEPLANO”.
 La representación de los monomios se puede realizar con cada una de las
piezas del ALGEPLANO
 Los estudiantes tienen un cuadrado grande (azul), si hacemos que “x”
represente la longitud de uno de sus lados, entonces el área azul se
representaría con “x2”
”.
x2
x
x
 Del mismo modo se procede a representar los valores que puede asumir el cuadrado
pequeño color amarillo.
y2
1
1
 Así mismo el área del rectángulo color verde podría representarse por “x” ya que sus lados
corresponden a “x” y a “1”.
y
x xy

8. Polinomios con una variablePolinomios con una variable
“x”“x”
+ +2
3 5 7x x 2
2x + 3x

9. X2
-X2
Cero

10. En la factorización determinaremos el
valor de cada lado de un arreglo
rectangular, para esto se tiene como
dato el valor del área del arreglo. La
siguiente actividad ilustra el método
más sencillo de factorizar un polinomio.

11. ACTIVIDAD Nº 1
Factorizar el polinomio 2
6 5x x+ +
1x +
5x +
( ) ( )2
6 5 5 1x x x x+ + = + +

12. ACTIVIDAD Nº 2
Factorizar el polinomio
2
2 7 6x x+ +
2x +
2 3x +
( ) ( )2
2 7 6 2 3 2x x x x+ + = + +

13. ACTIVIDAD Nº 3
Factorizar un polinomio cuando algunos de
sus términos son negativos. Por ejemplo,
factorizar
2
6x x− −

14. 2x +
3x −
( ) ( )2
6 3 2x x x x− − = − +

15. ACTIVIDAD Nº 4
Factorizar 2
2 3x x+ −
3x +
1x −
( ) ( )2
2 3 3 1x x x x+ − = + −