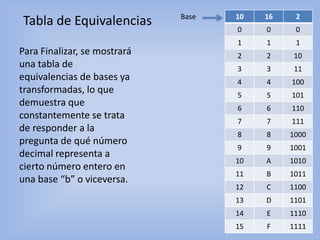
El documento presenta tres casos de algoritmos para transformar números entre diferentes bases numéricas. El primer caso explica cómo convertir números enteros de una base b a números enteros en base 10. El segundo caso trata sobre números fraccionarios. El tercer caso explica cómo convertir números enteros en base 10 a números enteros en una base b usando división repetida. Se incluye una tabla de equivalencias de números en diferentes bases como ejemplo.

1. Algoritmos de Transformación
Por: César Cisternas Peralta
Curso: Computación Aplicada
Sección N°: 2

2. Para todos los casos, se utilizará un
Algoritmo General:
Caso 1: Número entero en base “b” donde b es
un entero, a N° entero de base 10.
Algoritmo General
N M N,M= N° enteros
(b) (10)
b>1, b ϵ N° naturales n= N° dígitos de M
b= base

3. 0 1 2 n-1
M = d * b + d * b + d * b….d * b
(10) 0 1 2 n-1
Ejercicios de ejemplo:
4 3 2 1 0
1) (10001) ( ) = 1*2 + 0*2 + 0*2 + 0*2 + 1*2
(2) (10)
= 16+1 = 17
(10)
3 2 1 0
2) (4321) = 4*5 + 3*5 + 2*5 + 1*5 = 500 + 75 + 10 + 1
(5) = 586
(10)

4. Caso 2: N° fraccionarios en base “b” a N° fraccionario
base 10
N M N,M= N° fraccionarios
(b) (10)
b>1, b ϵ N° naturales n= N° dígitos
fraccionarios

5. Ejercicios de ejemplo:
-1 -2 -3
1) (0,101) ( ) = 1*2 + 0*2 + 1*2
(2)
-1, -2, -3…
= ½ + 0 + 1/8 = 5/8 = 0,625
(10)
-1 -2 -3
2) (0,237) = 2*8 + 3*8 + 7*8
(8)
= 2/8 + 3/64 + 7/512 = 159/512 ≈ 0,31054..
(10)

6. Caso 3: N° entero en base 10 a N° entero en base b
(Algoritmo de División).
En este caso, el N° en base 10 se divide por la base b hasta que el resultado sea igual a
0.
Ejemplo: Restos Los restos de cada división
conformarán el número
1) (16) ( ) 16:2 = 8 0 transformado desde base 10
(10) (2) 0 a base b (en este caso, base
2), escribiéndolos tal como
8:2 = 4 0
0 indica la dirección de la
flecha.
4:2 = 2 0
0
2:2 = 1 0 Por tanto, el resultado en
0 base 2 es:
1:2 = 0 1
(10000)
1
(2)

7. Base 10 16 2
Tabla de Equivalencias 0 0 0
1 1 1
Para Finalizar, se mostrará 2 2 10
una tabla de 3 3 11
equivalencias de bases ya 4 4 100
transformadas, lo que 5 5 101
demuestra que 6 6 110
constantemente se trata
7 7 111
de responder a la
8 8 1000
pregunta de qué número
9 9 1001
decimal representa a
10 A 1010
cierto número entero en
11 B 1011
una base “b” o viceversa.
12 C 1100
13 D 1101
14 E 1110
15 F 1111

8. Esperando que el material entregado sea de su agrado y
utilidad, me despido hasta una nueva ocasión
César Cisternas Peralta
Estudiante Ingeniería Civil Industrial
Universidad Tecnológica Metropolitana
2013