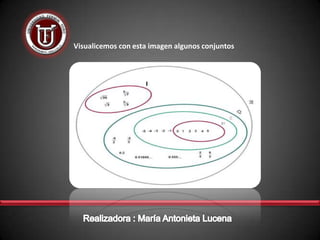
El documento define conceptos básicos de conjuntos como el conjunto universal U, la notación para conjuntos y elementos, y subconjuntos. Explica que un conjunto A es subconjunto de B si todos los elementos de A también están en B, denotado por A ⊆ B. También define el conjunto potencia de un conjunto A como el conjunto de todos sus subconjuntos, denotado por P(A).

1. Conjunto será cualquier colección de objetos y conjunto
universal, al conjunto que contiene todos los elementos a
considerar, denotado por la letra U .
Generalmente, los conjuntos son denotados con letras
mayúsculas como A,B,C,X,Y,Z, etc., mientras que para los
elementos se usan minúsculas como a,b,c,d,x,y,z, etc. Los
elementos de un conjunto son encerrados entre llaves o en un
círculo, el cual es llamado diagrama de Venn.

2. Visualicemos con esta imagen algunos conjuntos

3. Subconjuntos
Relación de Inclusión
Si A es el conjunto formado por todos los Estudiantes de Ing. de
Mantenimiento Mecánico y B es el conjunto formado por todos los
Estudiantes de la Universidad Fermín toro entonces, tenemos que
todo elemento de A es también elemento de B. Este resultado lo
expresamos diciendo que el conjunto A está incluido o contenido en el
conjunto B, o bien, que A es un subconjunto de B. Esta nueva relación
se simboliza por A Ì B.
Definición: Sean A y B conjuntos. Diremos que A es subconjunto de B
lo cual denotaremos por A Ì B, si todo elemento de A es también un
elemento de B.

4. Visualicemos con esta imagen como se relacionan los subconjuntos

5. Conjunto Potencia
Si A es un conjunto, se define el conjunto Potencia de A o conjunto partes de A
como Ã(A) = { X / X Ì A}, es decir, es el conjunto formado por todos los subconjuntos
de A.
Ejemplo: Si A = {x,y,z} entonces
Ã(A) = {{f }, {x}, {y}, {z}, {x,y}, {x,z}, {y,z}, {x,y,z}}
Características del Conjunto Potencia
-La principal característica de este conjunto es que es un conjunto de conjuntos,
-es decir, sus elementos son conjuntos.
-Dado un conjunto A podemos conocer el número de elementos de à (A),
-ya que si A tiene n elementos, entonces Ã(A) tiene 2n elementos.

6. Visualicemos con esta imagen como se relacionan los conjunto de
potencia

7. Igualdad de Conjuntos
Si dos conjuntos tienen los mismos elementos diremos que son iguales,
por ejemplo: A = {2,3,5,9,10} y B = {10,5,3,2,9} son iguales.

8. Unión e Intersección de Conjuntos
Sean A y B dos conjuntos. Se define la unión de
A y B como el conjunto:
A U B = { xÎ U / xÎ A Ú xÎ B}
Es decir, son todos los elementos que están en
A o están en B.
Ejemplo: Si A = {1,3,5,6,7,8} y B = {0,1,-
14,5,8,7,10} entonces,
A U B = {0,1,3,5,6,7,8,10,-14}

9. Diferencia y Complemento
Si A y B son conjuntos, entonces se define la
diferencia entre A y B como el siguiente
conjunto:
A - B = { xÎ U / xÎ A Ù xÏ B}. Es decir, son todos
los elementos que están en A pero que no
están en B.

10. Producto Cartesiano
Sean A y B dos conjuntos. Se define el
conjunto producto o producto cartesiano de A
y B como el conjunto Ax B = { (a,b) / aÎ B Ù bÎ B}
Ejemplo: Si A = {a,b} y B = {1,5,8}
entonces Ax B =
{(a,1), (a,5), (a,8), (b,1), (b,5), (b,8)}
mientras que BxA =
{(1,a), (1,b), (5,a), (5,b), (8,a),(8,b)}
Nótese que Ax B ¹ Bx A