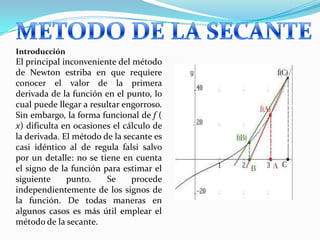
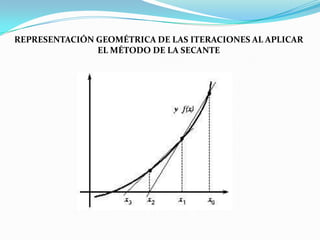
Este documento describe el método numérico de la secante para encontrar raíces de funciones. El método de la secante es similar al método de regula falsi, pero no considera los signos de la función. Usa dos puntos iniciales para estimar la derivada como la pendiente de la recta que pasa por esos puntos. Luego, calcula el siguiente punto iterativamente usando esa pendiente hasta converger a una solución dentro de un error especificado. Finalmente, presenta ejemplos y aplicaciones prácticas del método en Octave.

1. Universidad nacional de lojaAREA DE LA ENERGIA , LAS INDUSTRIAS Y LOS RECURSOS NATURALES NO RENOVABLESIngeniería en SistemasAnálisis NuméricoMÉTODO DE LA SECANTEIntegrantes:Andrés Armijos

2. Pedro aponte

3. Soraya Carrión

4. Diego castillo

5. Erasmo Montaño

6. Cristian palacios

7. Miguel paredesVIII módulo “A”

8. METODO DE LA SECANTEIntroducciónEl principal inconveniente del método de Newton estriba en que requiere conocer el valor de la primera derivada de la función en el punto, lo cual puede llegar a resultar engorroso. Sin embargo, la forma funcional de f ( x) dificulta en ocasiones el cálculo de la derivada. El método de la secante es casi idéntico al de regula falsi salvo por un detalle: no se tiene en cuenta el signo de la función para estimar el siguiente punto. Se procede independientemente de los signos de la función. De todas maneras en algunos casos es más útil emplear el método de la secante.

9. Una forma de evitar el cálculo de f ' ( x) consiste en considerar como aproximación a la derivada la recta que pasa por los valores de 2 iteraciones sucesivas (estima la f (x ) − f ( x ) tangente) es decir, la pendiente de la recta) :Esta variante se conoce con el nombre de método de la Secante. Sustituyendo esta expresión en la ecuación del método de Newton, se obtiene la expresión del método de la secante que proporciona el siguiente punto de iteración: