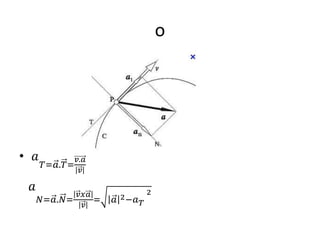
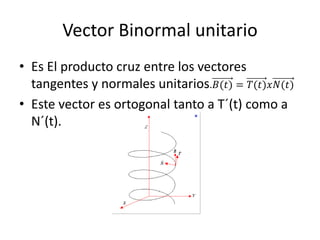
Este documento describe funciones vectoriales y sus aplicaciones en el movimiento en el espacio. Explica que una función vectorial mapea números reales a vectores y cómo calcular la derivada e integral de tales funciones. También cubre conceptos como la velocidad, aceleración y curvatura de curvas paramétricas definidas por funciones vectoriales, y cómo descomponer la aceleración en componentes tangenciales y normales. Incluye ejemplos numéricos para ilustrar estos conceptos.

1. APLICACIONES FUNCIONES
VECTORIALES

2. FUNCIONES VECTORIALES
• Una función vectorial es una función que
transforma un número real en un vector:
F : R → R3, definida como F(t) = (x(t), y(t), z(t)),
donde x(t), y(t) y z(t) son funciones reales de
variable real.
Así, se dice que F es continua, derivable o
integrable, si lo son x(t), y(t) y z(t).

3. DERIVADA E INTEGRAL DE UNA
FUNCION VECTORIAL

4. Reglas de derivación de funciones vectoriales
relacionadas con las operaciones entre vectores

6. Movimiento en el espacio
Cuando una función vectorial definida en un intervalo
abierto de R es derivable indefinidamente y su primera
derivada no se anula, decimos que se trata de una curva
regular.
Al vector F(t) se le llama vector de posición de la curva
Al vector F´(t) se le llama vector velocidad .
Al vector F´´(t) se le llama vector aceleración. De
modo que la velocidad en un instante t es F´(t) y la
aceleración es kF(t)k. .
Al vector F´(t) también se le llama vector tangente a la
curva F(t) en t.

7. EJEMPLO 1
• Dibuje la curva plana con la siguiente ecuacion
vectorial.
• Calcule 𝑟 ´(𝑡)
• Dibuje el vector de posición 𝑟 (𝑡) y el vector
tangente para el valor dado t.
𝑟 (𝑡)=(1+t)i+𝑡2
j, en t = 1

8. EJEMPLO 2
Hallar 𝑟 (𝑡) bajo las condiciones que se
especifican.
𝑟 (𝑡)´=2tj + 𝑡𝑘
𝑟 (0) = 𝑖 + 𝑗

9. EJEMPLO 3
Hallar la velocidad, la rapidez y la aceleración de
esa partícula.
𝑟 (𝑡)=ti+(2t-5)j+3tk

10. EJEMPLO 4
Hallar la posición en el instante t=2.
𝑎 𝑡 = 𝑡𝑗 + 𝑡𝑘, 𝑣 1 = 5𝑗, 𝑟 1 = 0

11. Vector tangente unitario
• Si 𝑟 (𝑡) es el vector de posición de una curva C
en un punto P de C el vector tangente unitario
de C en P, denotado por T(t), es el vector
unitario en la dirección 𝑟´ (𝑡), si 𝑟´ (𝑡)≠0 .
𝑇 (𝑡)=
𝑟´ (𝑡)
𝑟´ (𝑡)
=
𝑣 (𝑡)
𝑣(𝑡)

12. Vector unitario normal
• Cuando los dos vectores unitarios T y N están
trazados por el punto de la curva f(t), determinan
un plano llamado osculador de la curva.
• El plano osculador es el plano que mejor se
adapta a la curva en cada uno de sus puntos. Si la
curva es plana, el plano osculador coincide con el
plano de la curva.

13. Componentes Tangencial y Normal de
la aceleración
• El vector velocidad v es tangente a la trayectoria.
• El vector aceleración a puede descomponerse en
dos componentes (llamadas componentes
intrínsecas)mutuamente perpendiculares: una
componente tangencial (en la direcciónde la
tangente a la trayectoria), llamada aceleración
tangencial, y una componente normal (en la
dirección de la normal principal a la trayectoria),
llamada aceleración normal o centrípeta (este
último nombre en razón a que siempre está
dirigida hacia el centro de curvatura).

14. o
• 𝑎
𝑇=𝑎.𝑇=
𝑣.𝑎
𝑣
𝑎
𝑁=𝑎.𝑁=
𝑣𝑥𝑎
𝑣
= 𝑎 2−𝑎 𝑇
2

15. Vector Binormal unitario
• Es El producto cruz entre los vectores
tangentes y normales unitarios.𝐵(𝑡) = 𝑇(𝑡)𝑥𝑁(𝑡)
• Este vector es ortogonal tanto a T´(t) como a
N´(t).

16. Ejemplo
• Hallar 𝑎 𝑇 , 𝑎 𝑵 , 𝑇 (𝑡), 𝑁 (𝑡) en el instante t
dado, para la curva especial
𝑟 (𝑡)=ti+2tj-3tk,t=1

17. Longitud de arco de curva
La longitud de un arco de curva entre dos
puntos F(a) y F(b) viene dada por la formula.

18. Curvatura
Se define la curvatura como “la variación del
vector tangente con respecto a la longitud del
arco.
La curvatura viene a medir como se ”tuerce“ la
curva respecto de su longitud. Para curvas, no
necesariamente parame trizadas por el arco, se
puede calcular como:

19. Componentes de la aceleración
• Componente normal
𝑎𝑁 = 𝑘 𝑣 2
=
𝑟´ 𝑡 𝑥 𝑟´´(𝑡)
𝑟´(𝑡)
• Componente tangencial
aT= 𝑣 ´=
𝑣.𝑎
𝑣
=
𝑟´ 𝑡 .𝑟´´(𝑡)
𝑟´(𝑡)
• La componente tangencial de la aceleración es la responsable
de que cambie la rapidez, mientras que la componente
normal es responsable por la curvatura de la trayectoria. 𝑎 =
𝑎 𝑡 𝑇+𝑎 𝑁 𝑁

20. • Si la curva está en el espacio, también se
“retuerce” y para medir esto se define la
torsión como: