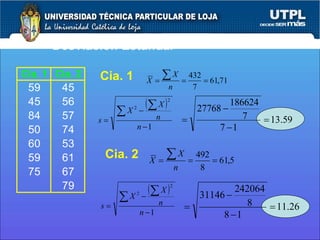
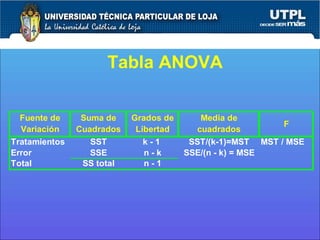
Este documento resume los conceptos clave detrás del análisis de varianza (ANOVA) y las pruebas estadísticas F y t. Explica cómo ANOVA compara tres o más medias poblacionales para determinar si son iguales, mientras que las pruebas F y t se usan para comparar varianzas poblacionales y pares de medias, respectivamente. Proporciona ejemplos numéricos para ilustrar cómo aplicar estos métodos y realizar inferencias estadísticas.

1. ESTADISTICA ANÁLISIS DE VARIANZA Cúmar Cueva

2. Comparación de dos Varianzas Poblacionales

3. LA DISTRIBUCIÓN F Sir Ronald Fisher Muestras  Poblaciones con igual Varianza Comparar varias medias poblacionales (ANOVA)

4. Características Continua  Valores infinitos No puede ser negativa Positivamente Sesgada (derecha) Asintótica (aumenta x pero no toca el eje) Existe una familia de Distribuciones F (grados de libertad)

5. Pasos para Comparar dos Varianzas Poblacionales Hipótesis Nula Alternativa

6. 2. Nivel de Significancia  : Probabilidad de rechazar la hipótesis nula. Un valor entre 0 – 1, usualmente 0.05 – 0.01 3. Grados de Libertad y Valor Crítico (n-1) Según los grados de libertad( numerador y denominador) se ubica el valor crítico en la tabla G.

7. 4. Se extrae el valor de prueba: El valor resultante se compra con el valor crítico (F), si es mayor se rechaza la hipótesis nula.

8. Ejemplo: Cantidad de productos con fallas en dos empresas fabricantes de juguetes. ¿Existe alguna diferencia en la variación en cuanto a la cantidad de fallas?

9. Desviación Estándar Cia. 1 Cia. 2

10. Observación: La extracción de la desviación estándar indica que hay más variación en la Cia. 1 13.59 > 11.26 A continuación se comprobará con una prueba estadística.

11. 1. Hipótesis Se plantea que: 2. Nivel de Significancia:  = 0.10

12. 3. Grados de Libertad y Valor Crítico  = 0.05 Localizamos el valor crítico según los grados de libertad en numerador y denominador: 3.87

13. 4. Se extrae el valor de prueba: Valor menor al valor crítico.

14. Interpretación 1.46 < 3.87 Valor calculado (1.46) es menor que el valor crítico (3.87). Por tanto se acepta la hipótesis nula. Por tanto no existe variación en cuanto a la cantidad de fallas entre las dos compañías.

15. ANOVA (Analisys of Variance)

16. Características y Supuestos implícitos Compara 3 o más medias poblacionales si son iguales. Evita la propagación del error. Las muestras provienen de poblaciones con una distribución normal. Las desviaciones estándar de las poblaciones son iguales. Las muestras son independientes.

17. Tabla ANOVA

18. De donde, Suma de Cuadrados, TOTAL x = cada una de las observaciones n = número total de observaciones

19. Suma de Cuadrados debidos al Tratamiento T c total de la columna de cada tratamiento. n c número de observaciones de cada tratamiento

20. Suma de Cuadrados al ERROR Ejemplo 

21. Control de Peso con tres Dietas. Se seleccionó aleatoriamente a 15 pacientes y se asignó 5 a cada dieta. Después de tres semanas se registró la perdida de peso, en libras. Al nivel de Significancia 0.05 ¿puede concluirse que hay alguna diferencia entre las 3 dietas?

22. 1. Hipótesis 2. Nivel de Significancia:  = 0.05 H 1 : Los promedios de peso no son iguales.

23. 3. Grados de Libertad y Valor Crítico  = 0.05 Localizamos el valor crítico según los grados de libertad en numerador y denominador: 3.89

24. 4. Cálculos para tabla ANOVA

25. Determinamos:

26. Reemplazando en la Tabla ANOVA

27. Interpretación 13.47 > 3.89 Valor calculado (13.47) es mayor que el valor crítico (3.89). Por tanto se desecha la hipótesis nula. Se determina que si existe diferencia entre las medias de peso para cada dieta.

28. Pero… Cómo saber cual de las medias es mayor o menor ?

29. Inferencia acerca de pares de valores medios

30. Características Se determina entre grupos en los cuales haya diferencia. Si el intervalo de confianza incluye el cero, no hay diferencia entre las medias de tratamiento.

31. Fórmula Media de la 1er y 2da muestras t obtenido de los grados de libertad (n-k) MSE cuadrado medio del error n 1 y n 2 número de observaciones de las muestras

32. Ej. Inferencia entre la primera y tercera dieta

33. Conclusión: El intervalo de confianza no incluye el cero, por tanto existe una gran diferencia en el tratamiento. Más perdida de peso en la dieta 3

34. ?