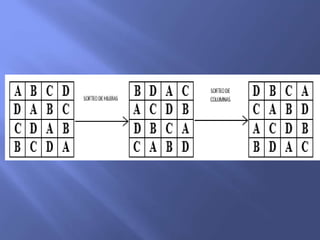
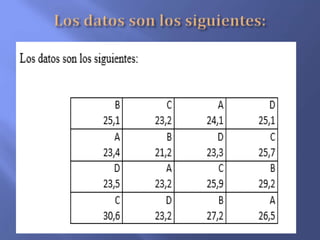
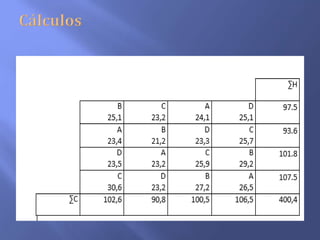
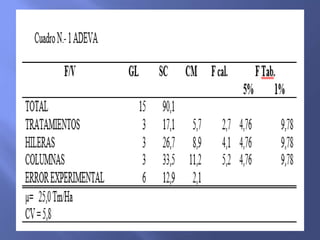
El documento describe la metodología de un diseño de bloques completos al azar (DBCA) para investigaciones agronómicas, destacando la importancia de la homogeneidad del material y la aleatoriedad en la distribución de tratamientos. Se mencionan pasos para la planificación y ejecución, así como la fórmula para analizar los resultados mediante análisis de varianza, concluyendo que no se observaron diferencias de rendimiento entre tratamientos evaluados. Además, se señala que se deben tener cuidados específicos en la cantidad de tratamientos y el diseño experimental para obtener resultados significativos.

1. Ing. Verónica Taipe, MS.c.

2. Se utiliza en
investigaciones
cuando se encuentra
dos fuentes de
variabilidad

3. En el campo o laboratorio
Lugares donde hay dos factores que esta
afectando sea positiva o negativamente la
aplicación de los tratamientos.

4. Que el material sea lo
más homogéneo posible
Que la distribución sea
totalmente al azar
Como es cuadrado debe
haber igual número de
tratamientos, hileras y
columnas

5. Sencillo de planificar y ejecutar
Permite la estratificación simultanea dentro de una
misma hiera como la columna, siendo más eficiente que
el DCA y DBCA
Permite el cálculo de una o más unidades perdidas

6. El número de tratamientos no
debe ser elevado (4 – 6)
No es recomendable para
pocos tratamientos dado que
los GL del error experimental
son muy bajos.

7. Xijk = µ + Ti + βj +δk + Eijk
• i = 1… t tratamientos
• j = 1.. h hileras
• K = 1.. c columnas
Una observación cualquiera, es
igual al efecto del promedio
poblacional del factor en estudio,
más el efecto que provoca la
aplicación de los tratamientos, más
el efecto que provoca la
implementación las hileras, mas el
efecto que provoca las columnas y
más el efecto del error
experimental.

9. 1.- Se busca el CL patrón en los libros de
estadística
2.- Ningún tratamiento debe repetirse dentro de
una misma hiera ni dentro de una misma
columna
3.- Una vez seleccionado el patrón se procede a
sortear las hileras y columnas
4.- Una vez sorteado se implementa en el sitio
experimental

11. En un experimento bajo el DCL se comparó la
adaptación de 4 variedades de un cultivar, siendo la
variable en estudio rendimiento (kg/parcela).

12. Los datos son los siguientes:

13. Problema:
Experimental:
Factor en estudio:
Tratamientos:

14. Número de hileras:
Número de columnas:
Unidad experimental:
Variable:
Hipótesis:

21.  En el análisis de varianza se puede observar que NO
hay diferencias entre los tratamientos ya que la Fcal
es MENOR que la Ftab, con probabilidad de error
de 0.05. Por lo tanto TODOS los tratamientos tienen
un rendimiento igual.

24. Fórmula para promedios cuando se pierden
dos o más unidades experimentales