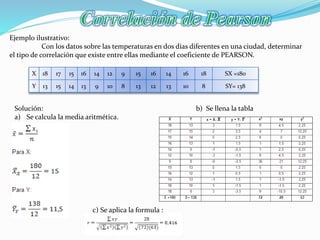
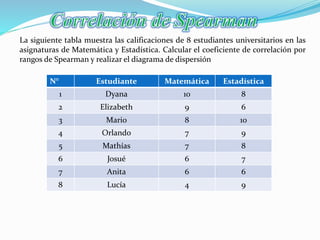
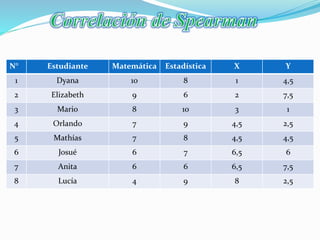
El documento explica el coeficiente de correlación de Pearson y Spearman. El coeficiente de Pearson mide la relación lineal entre dos variables cuantitativas, variando de -1 a 1, donde 1 indica correlación positiva perfecta, -1 negativa perfecta y 0 ninguna correlación lineal. El coeficiente de Spearman se usa para variables ordinales y también varía de -1 a 1.

1. Republica Bolivariana de Venezuela
Ministerio del Poder Popular para la Educación
Instituto Universitario Politécnico
“Santiago Mariño
Sede Barcelona
Estado Anzoátegui
Profesor: Bachiller.
Pedro Beltrán Yendry Montaño
C.I: 25.844.454
Sección” CV”

2. El coeficiente de correlación de Pearson es una medida de la
relación lineal entre dos variables aleatorias cuantitativas. A diferencia de la
covarianza, la correlación de Pearson es independiente de la escala de
medida de las variables.
Son números que varían entre los límites +1 y -1. Su magnitud
indica el grado de asociación entre las variables; el valor r = 0 indica que no
existe relación entre las variables; los valores ( 1 son indicadores de una
correlación perfecta positiva (al crecer o decrecer X, crece o decrece Y) o
negativa (Al crecer o decrecer X, decrece o crece Y).
De manera menos formal, podemos definir el coeficiente de
correlación de Pearson como un índice que puede utilizarse para medir el
grado de relación de dos variables siempre y cuando ambas sean
cuantitativas.

3. En el caso de que se esté estudiando dos variables aleatorias X y Y sobre una
población; el coeficiente de correlación de Pearson se simboliza con la letra Ρx,y,
siendo la expresión que nos permite calcularlo:
Donde:
De manera análoga podemos calcular este coeficiente sobre n estadístico muestral,
denotado como a:

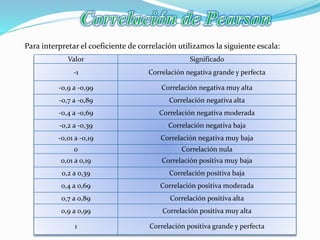
4. El valor del índice de correlación varía en el intervalo [-1,1]:
Si r = 1, existe una correlación positiva perfecta. El índice indica una
dependencia total entre las dos variables denominada relación directa:
cuando una de ellas aumenta, la otra también lo hace en proporción
constante.
Si 0 < r < 1, existe una correlación positiva.
Si r = 0, no existe relación lineal. Pero esto no necesariamente implica
que las variables son independientes: pueden existir todavía relaciones
no lineales entre las dos variables.
Si -1 < r < 0, existe una correlación negativa.
Si r = -1, existe una correlación negativa perfecta. El índice indica una
dependencia total entre las dos variables llamada relación inversa:
cuando una de ellas aumenta, la otra disminuye en proporción constante

5. Valor Significado
-1 Correlación negativa grande y perfecta
-0,9 a -0,99 Correlación negativa muy alta
-0,7 a -0,89 Correlación negativa alta
-0,4 a -0,69 Correlación negativa moderada
-0,2 a -0,39 Correlación negativa baja
-0,01 a -0,19 Correlación negativa muy baja
0 Correlación nula
0,01 a 0,19 Correlación positiva muy baja
0,2 a 0,39 Correlación positiva baja
0,4 a 0,69 Correlación positiva moderada
0,7 a 0,89 Correlación positiva alta
0,9 a 0,99 Correlación positiva muy alta
1 Correlación positiva grande y perfecta
Para interpretar el coeficiente de correlación utilizamos la siguiente escala:

6. a) Para datos no agrupados se calcula aplicando la siguiente
ecuación:
r:Coeficiente producto-momento de correlación lineal

7. Ejemplo ilustrativo:
Con los datos sobre las temperaturas en dos días diferentes en una ciudad, determinar
el tipo de correlación que existe entre ellas mediante el coeficiente de PEARSON.
X 18 17 15 16 14 12 9 15 16 14 16 18 SX =180
Y 13 15 14 13 9 10 8 13 12 13 10 8 SY= 138
Solución:
a) Se calcula la media aritmética.
b) Se llena la tabla
c) Se aplica la formula :

8. b) Para datos agrupados, el coeficiente de Correlación de
Pearson se calcula aplicando la siguiente fórmula:
Donde:
n = número de datos.
f = frecuencia de celda.
fx = frecuencia de la variable X.
fy = frecuencia de la variable Y.
dx = valores codificados o cambiados para los intervalos de la variable X, procurando
que al intervalo central le corresponda dx = 0, para que se hagan más fáciles los
cálculos.
dy = valores codificados o cambiados para los intervalos de la variable X, procurando
que al intervalo central le corresponda dy = 0, para que se hagan más fáciles los
cálculos.

9.  Permite predecir el valor de una variable dado un valor determinado de la otra
variable.
 Se trata de valorar la asociación entre dos variables cuantitativas estudiando el
método conocido como correlación.
 Dicho calculo es el primer paso para determinar la relación entre las variables.
 Consiste en la posibilidad de calcular su distribución muestral y asi poder
determinar su error típico de estimación.
 Reporta un valor de correlación cercano a 0 como un indicador de que no hay
relación lineal entre 2 variables.

10.  El valor del coeficiente de correlación es independiente de
cualquier unidad usada para medir variables.
 Mientras mas grande sea la muestra mas exacta será la
estimación.
 Requiere supuestos acerca de la naturaleza o formas de
las poblaciones afectadas.
 Requiere que las dos variables hayan sido medidas hasta
un nivel cuantitativo continuo y que la distribución de
ambas sea semejante a la de la curva normal-

11. El coeficiente de correlación de Spearman, ρ (rho) es una medida de la correlación
(la asociación o interdependencia) entre dos variables aleatorias continuas. Para
calcular ρ, los datos son ordenados y reemplazados por su respectivo orden.
El estadístico ρ viene dado por la expresión:
donde D es la diferencia entre los correspondientes estadísticos de orden de x - y. N
es el número de parejas.
Este coeficiente se emplea cuando una o ambas escalas de medidas de las vaiables
son ordinales, es decir, cuando una o ambas escalas de medida son posiciones.
Ejemplo: Orden de llegada en una carrera y peso de los atletas.

12. Para muestras mayores de 20 observaciones, podemos utilizar la siguiente
aproximación a la distribución t de Student.
La interpretación de coeficiente de Spearman es igual que la del coeficiente de
correlación de Pearson. Oscila ente -1 y +1, indicándonos asociaciones negativas o
positivas respectivamente, “0” cero, significa no correlación pero no independencia.

13.  Se requiere que al menos las variables estén medidas en al menos escala ordinal
es decir de forma que las puntaciones que la representan puedan ser colocadas en
dos series ordenadas.
 Una generalización del coeficiente de sepearman es útil en la situación en la cual hay tres o
mas condiciones, varios individuos son observados en cada uno de ellas predecimos que
las observaciones tendrán un orden en particular.
 Para aplicar el coeficiente de correlación de Spearman se requiere que las variables estén
medidas al menos en escala ordinal, es decir, de forma que las puntuaciones que las
representan pueden ser colocadas en dos series ordenadas.

14.  No esta afectada por los cambios en las unidades de
medida.
 Al ser una técnica no parámetra, es libre de
distribución probabilística.
 Las variables se correlacionan de acuerdo al rango
de valores generados en cada distribución.
 Es recomendable usarlo cuando los datos presentan valores
extremos, ya que dichos valores afectan mucho el coeficiente
de correlación de Pearson, o ante distribuciones no
normales.
 r no debe ser utilizado para decir algo sobre la relación entre
causa y efecto.
 Es difícil estimar el coeficiente de correlación entre dos
distribuciones de formas diferentes. El mismo coeficiente de
correlación puede resultar en diferentes gráficos de puntos
para diferentes distribuciones correlacionadas.

15. La siguiente tabla muestra las calificaciones de 8 estudiantes universitarios en las
asignaturas de Matemática y Estadística. Calcular el coeficiente de correlación por
rangos de Spearman y realizar el diagrama de dispersión
N° Estudiante Matemática Estadística
1 Dyana 10 8
2 Elizabeth 9 6
3 Mario 8 10
4 Orlando 7 9
5 Mathías 7 8
6 Josué 6 7
7 Anita 6 6
8 Lucía 4 9

16. En la asignatura de Matemática se observa:
- Dyana tiene la más alta calificación, ocupando el primer puesto, por lo que su
rango es 1
- Elizabeth ocupa el segundo puesto, por lo que su rango es 2
- Mario se encuentra ubicado en el tercer lugar, por lo que su rango es 3
- Orlando y Mathías ocupan el cuarto y quinto puesto, por lo que su rango es la
media aritmética de 4 y 5 que da por resultado 4,5
- Josué y Anita ocupan el sexto y séptimo lugar, por lo que su rango es la media
aritmética de 6 y 7 que da por resultado 6,5

17. - Lucía se encuentra ubicada en el octavo lugar, por lo que su rango es 8
En la asignatura de Estadística se observa:
- Mario tiene la más alta calificación, ocupando el primer puesto, por lo que su rango
es 1
- Orlando y Lucía ocupan el segundo y tercer puesto, por lo que su rango es la media
aritmética de 2 y 3 que da por resultado 2,5
- Dyana y Mathías ocupan el cuarto y quinto puesto, por lo que su rango es la media
aritmética de 4 y 5 que da por resultado 4,5
- Josué se encuentra ubicado en el sexto lugar, por lo que su rango es 6
- Elizabeth y Anita ocupan el séptimo y octavo lugar, por lo que su rango es la media
aritmética de 7 y 8 que da por resultado 7,5

18. N° Estudiante Matemática Estadística X Y
1 Dyana 10 8 1 4,5
2 Elizabeth 9 6 2 7,5
3 Mario 8 10 3 1
4 Orlando 7 9 4,5 2,5
5 Mathías 7 8 4,5 4,5
6 Josué 6 7 6,5 6
7 Anita 6 6 6,5 7,5
8 Lucía 4 9 8 2,5

19. Calculando d, 𝑑2
, y 𝑑2
, se obtiene los siguientes resultados :
Aplicando la formula se obtiene :

20.  https://es.wikipedia.org/wiki/Coeficiente_de_correlaci%C3%B3n_de_
Pearson
 http://www.monografias.com/trabajos85/coeficiente-correlacion-karl-
pearson/coeficiente-correlacion-karl-pearson.shtml
 http://www.monografias.com/trabajos85/coeficiente-correlacion-
rangos-spearman/coeficiente-correlacion-rangos-spearman.shtml
 https://es.wikipedia.org/wiki/Coeficiente_de_correlaci%C3%B3n_de_S
pearman