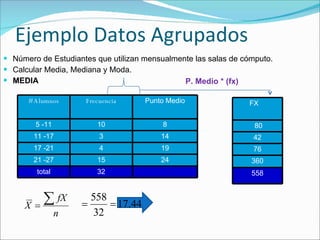
Este documento define y explica tres medidas de tendencia central: la media, la mediana y la moda. La media es la suma de todos los valores dividida por el número total de datos. La mediana es el valor central de los datos ordenados de menor a mayor. La moda es el valor que se repite con más frecuencia. El documento incluye ejemplos de cómo calcular estas medidas para datos agrupados y no agrupados.

1. MEDIDAS DE TENDENCIA CENTRAL Escuela: Ponentes: Bimestre: Ciclo: Ciencias de la Computación Cinthia Pulla E. Ma. Fernanda Valverde. II Bimestre Abril- Agosto 2008

2. Medidas de Tendencia Central

3. Media Aritmética Suma de todos los valores de la población, dividida para el número total de dichos datos. Para calcular utilizamos la siguiente fórmula, que es la misma para la MEDIA MUESTRAL Donde: u= Representa la media de los elementos N= Número total de elementos X= Representa los elementos. ∑ = Es la letra griega en mayúscula, indica la operación de sumar. ∑ X= Simboliza la suma de todos los valores X.

4. Media Ponderada. Se presenta cuando hay varias observaciones con un mismo valor, lo cual puede ocurrir si los datos se han agrupado en una distribucion de frecuencias. Cada observacion se multiplica por el numero de veces que se presenta.

5. Ejemplo- Media Ponderada Venta de Tarjetas para Telefonía Móvil(PORTA). Datos estimados Valor Tarjeta # de Compras 3 17 6 8 10 12 20 5 30 4

6. Resultado-Media. Ponderada

7. Mediana Es un valor único de un conjunto de datos que mide al elemento central en los datos. Este único elemento es el más cercano a la mitad o el más central en el conjunto de números. En los DATOS NO AGRUPADOS . Es el valor que corresponde al punto medio luego de ser ordenados de menor a mayor, donde el 50% deben ser mayores que la mediana y 50% menores.

8. Mientras que en los datos AGRUPADOS se rige a la siguiente fórmula. De donde, L  Limite inferior de la clase (mediana) n  Número total de frecuencias f  frecuencia de la clase (mediana) FA  frecuencia acumulada menor (mediana) i  amplitud de clase

9. Es una medida de tendencia central parecida a la mediana ya que no se calcula por métodos ordinarios de aritmética, Sino por simple observación. Valor que se repite más frecuentemente en un conjunto de datos. En DATOS AGRUPADOS se calcula mediante el punto medio de clase que contiene mayor número de frecuencia. Moda

10. Ejemplo Datos no Agrupados En la tabla se muestra el número de errores diarios en la facturación realizada por una compañía telefónica local, calcula la moda . 0, 2, 5, 7, 15, 0, 2, 5, 7, 15, 1, 4, 6, 8, 15, 1, 4, 6, 12, 19 Media = 134/20= 6.7 Mediana = 0, 0, 1, 1, 2, 2, 4, 4, 5, 5, 6, 6, 7, 7, 8, 12, 15, 15, 15, 19 = 5+ 6 /2 = 5.5 Moda = 15 .

11. Ejemplo Datos Agrupados Número de Estudiantes que utilizan mensualmente las salas de cómputo. Calcular Media, Mediana y Moda. MEDIA P. Medio * (fx) # Alumnos Frecuencia Punto Medio 5 -11 10 8 11 -17 3 14 17 -21 4 19 21 -27 15 24 total 32 FX 80 42 76 360 558

12. MODA n / 2 = 32 / 2 = 16 Localización: MEDIANA # Alumnos Frecuencia Frecuencia Acumulada 5 -11 10 10 11 -17 3 13 17 -23 4 17 23 -29 15 32 total 32

13. Gracias PREGUNTAS¿?