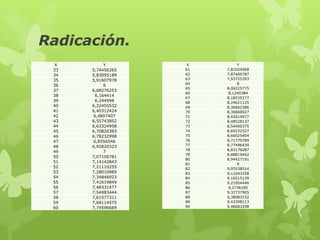
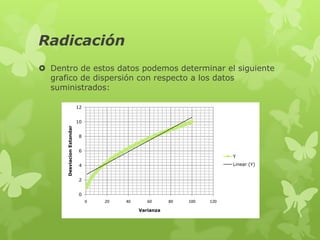
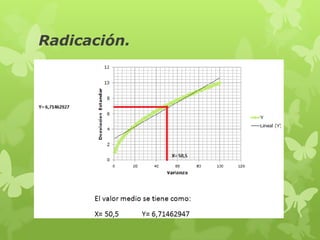
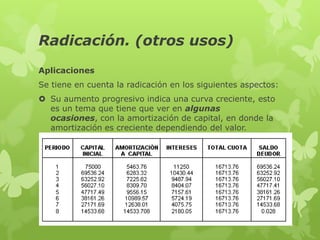
El documento aborda la aplicación de la radicación en finanzas y estadística, destacando su relevancia en el cálculo de la desviación estándar, una medida de dispersión crucial en estadística descriptiva. Se menciona cómo la raíz cuadrada de los valores se relaciona con gráficos de dispersión y el cálculo de varianza. Además, se mencionan aplicaciones prácticas de la radicación en la amortización de capital y en la comparación de valores futuros en inversiones.

1. Aplicación de la
radicación en el ámbito
financiero
Por: Yenith Lucero Garzón.
Corporación Universitaria Minuto de Dios

2. Radicación.
Se determina la siguiente información de la siguiente
manera:
X Y X Y
1 1
17 4,12310563
2 1,41421356
18 4,24264069
3 1,73205081 19 4,35889894
4 2
20 4,47213595
5 2,23606798
21 4,58257569
6 2,44948974
22 4,69041576
7 2,64575131 23 4,79583152
8 2,82842712 24 4,89897949
9 3
25 5
10 3,16227766
26 5,09901951
11 3,31662479
27 5,19615242
12 3,46410162 28 5,29150262
13 3,60555128 29 5,38516481
14 3,74165739 30 5,47722558
15 3,87298335 31 5,56776436
16 4 32 5,65685425

3. Radicación.
X Y X Y
33 5,74456265 61 7,81024968
34 5,83095189 62 7,87400787
35 5,91607978 63 7,93725393
64 8
36 6
65 8,06225775
37 6,08276253
66 8,1240384
38 6,164414
67 8,18535277
39 6,244998 68 8,24621125
40 6,32455532 69 8,30662386
41 6,40312424 70 8,36660027
42 6,4807407 71 8,42614977
43 6,55743852 72 8,48528137
44 6,63324958 73 8,54400375
45 6,70820393 74 8,60232527
46 6,78232998 75 8,66025404
47 6,8556546 76 8,71779789
48 6,92820323 77 8,77496439
78 8,83176087
49 7
79 8,88819442
50 7,07106781
80 8,94427191
51 7,14142843
81 9
52 7,21110255 82 9,05538514
53 7,28010989 83 9,11043358
54 7,34846923 84 9,16515139
55 7,41619849 85 9,21954446
56 7,48331477 86 9,2736185
57 7,54983444 87 9,32737905
58 7,61577311 88 9,38083152
59 7,68114575 89 9,43398113
60 7,74596669 90 9,48683298

4. Radicación.
X Y
91 9,53939201
92 9,59166305
93 9,64365076
94 9,69535971
95 9,74679434
96 9,79795897
97 9,8488578
98 9,89949494
99 9,94987437
100 10

5. Radicación
 Dentro de estos datos podemos determinar el siguiente
grafico de dispersión con respecto a los datos
suministrados:
12
10
Desviacion Estandar
8
6
Y
4 Linear (Y)
2
0
0 20 40 60 80 100 120
Varianza

6. Radicación.

7. Radicación.
 Dentro de los datos establecidos y organizados según la
grafica podemos determinar que:
 Ya que la raíz cuadrada de cada uno de los dígitos es el
equivalente al eje Y.

8. Radicación.
 Dentro de estos datos podemos definir
principalmente, que la radicación tiene una aplicación
especial en la estadística por medio de la desviación
estándar, una medida de dispersión muy utilizada en la
estadística descriptiva.
 Por tanto se tiene en cuenta que la desviación
estándar, es el resultado de la raíz cuadrada de la
varianza.

9. Radicación.
 Desviación estándar:
 La medida de dispersión que se conoce como
desviación estándar en estadística, es la raíz
cuadrada de las distancias de las observaciones con
respecto a su promedio, obteniendo como resultado las
mismas unidades en que están dados los datos
originales recolectados.
 Su formula es:

10. Radicación.
 Como ejemplo tenemos:

11. Radicación. (otros usos)
Aplicaciones
Se tiene en cuenta la radicación en los siguientes aspectos:
 Su aumento progresivo indica una curva creciente, esto
es un tema que tiene que ver en algunas
ocasiones, con la amortización de capital, en donde la
amortización es creciente dependiendo del valor.

12. Radicación.
 También la radicación es utilizada en inversiones, para
la comparación de valores futuros que son alternos o
paralelos a través del tiempo de espera.

13. Radicación.
 También se tiene en cuenta la Radicación para el despeje
de la ecuación general de interés compuesto, en donde:

14. Radicación
FIN