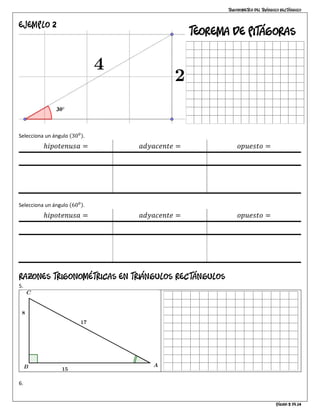
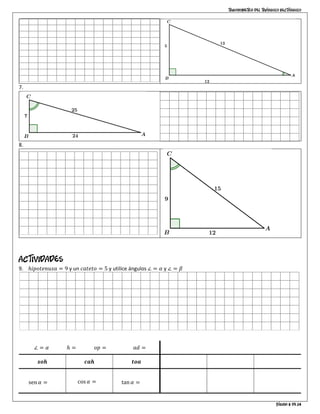
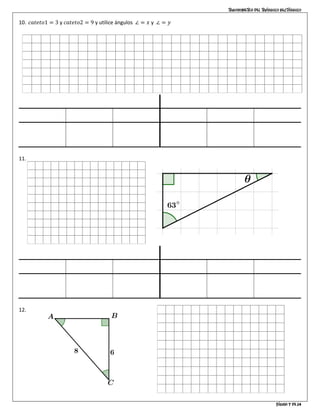
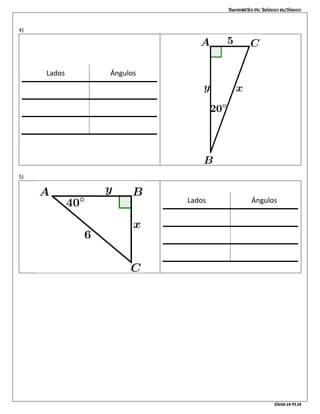
El documento es una guía sobre trigonometría en triángulos rectángulos, explicando la nomenclatura de los lados (hipotenusa, opuesto y adyacente) y sus relaciones a través de funciones trigonométricas (seno, coseno y tangente). Incluye el teorema de Pitágoras y una serie de ejemplos y actividades para ayudar a los estudiantes a aplicar los conceptos aprendidos. Se abordan problemas relacionados con la identificación de los lados y el cálculo de longitudes usando las razones trigonométricas.

1. Trigonometría del triángulo rectángulo
Página 1 de 14
Escuela Normal Superior de Villavicencio
NOMBRE DEL ESTUDIANTE: ____________________________________________________
ÁREA: TRIGONOMETRÍA GRADO: DÉCIMO -__ FECHA: _______
DOCENTE: ARMANDO GONZÁLEZ PERÍODO: 2 GUÍA: 01
Lados de triángulos rectángulos
Utilizamos palabras especiales para designar los lados de triángulos
rectángulos.
La hipotenusa de un triángulo rectángulo es siempre el lado opuesto
al ángulo recto. Es el lado más grande de un triángulo rectángulo.
Los otros dos lados se llaman opuesto y adyacente. Los nombres están
dados por su relación con respecto a un ángulo.
El lado opuesto está siempre enfrente del ángulo dado.
El lado adyacente es el que está junto al ángulo dado, y que no
es la hipotenusa.

2. Trigonometría del triángulo rectángulo
Página 2 de 14
Combinando todo esto, los nombres de los lados son como sigue:
Es importante recordar que, si pensamos en otro ángulo, nuestros lados
opuesto y adyacente cambian, pero nuestra hipotenusa no.
actividad
1. Con respecto al ángulo 𝐸 y 𝐴, nombre la hipotenusa, el opuesto y el adyacente, de cada ángulo
2. Con respecto al ángulo 𝑃 y 𝑅, nombre la hipotenusa, el opuesto y el adyacente.
3. Con respecto al ángulo 𝑌 y 𝐾, nombre la hipotenusa, el opuesto y el adyacente.
Ángulo ℎ𝑖𝑝𝑜𝑡𝑒𝑛𝑢𝑠𝑎 𝑜𝑝𝑢𝑒𝑠𝑡𝑜 𝑎𝑑𝑦𝑎𝑐𝑒𝑛𝑡𝑒
∠𝑬 𝑬𝑨̅̅̅̅ 𝑴𝑨̅̅̅̅̅ 𝑬𝑴̅̅̅̅̅
∠𝑨 𝑬𝑨̅̅̅̅ 𝑬𝑴̅̅̅̅̅ 𝑨𝑴̅̅̅̅̅
Ángulo ℎ𝑖𝑝𝑜𝑡𝑒𝑛𝑢𝑠𝑎 𝑜𝑝𝑢𝑒𝑠𝑡𝑜 𝑎𝑑𝑦𝑎𝑐𝑒𝑛𝑡𝑒
∠𝑷 𝑷𝑹̅̅̅̅ 𝑸𝑹̅̅̅̅ 𝑷𝑸̅̅̅̅
∠𝑹 𝑷𝑹̅̅̅̅ 𝑷𝑸̅̅̅̅ 𝑹𝑸̅̅̅̅
Ángulo ℎ𝑖𝑝𝑜𝑡𝑒𝑛𝑢𝑠𝑎 𝑜𝑝𝑢𝑒𝑠𝑡𝑜 𝑎𝑑𝑦𝑎𝑐𝑒𝑛𝑡𝑒
∠𝒀 𝑲𝒀̅̅̅̅ 𝑲𝑺̅̅̅̅ 𝒀𝑺̅̅̅̅
∠𝑲 𝑲𝒀̅̅̅̅ 𝑺𝒀̅̅̅̅ 𝑲𝑺̅̅̅̅
Pintarsiemprelostriángulosdelasactividades.

3. Trigonometría del triángulo rectángulo
Página 3 de 14
Identifiquemos lo aprendido hasta ahora.
Recuerda que solo se puede hablar de hipotenusa cuando hay triángulos rectángulos.
Por Teorema de Pitágoras, tenemos:
ℎ𝑖𝑝𝑜𝑡𝑒𝑛𝑢𝑠𝑎 2
= 𝑐𝑎𝑡𝑒𝑡𝑜 2
+ 𝑐𝑎𝑡𝑒𝑡𝑜 2
⟹ 52
= 32
+ 42
En trigonometría 3 funciones centrales, que permite establecer las relaciones entre las tres medidas de los lados del
triángulo rectángulo.
Razón Abreviatura
𝑆𝑒𝑛𝑜 𝑠𝑒𝑛
𝐶𝑜𝑠𝑒𝑛𝑜 𝑐𝑜𝑠
𝑇𝑎𝑛𝑔𝑒𝑛𝑡𝑒 𝑡𝑎𝑛
Mnemotecnia
𝑠𝑒𝑛 𝑐𝑜𝑠 𝑡𝑎𝑛
𝑠𝑜ℎ 𝑐𝑎ℎ 𝑡𝑜𝑎
𝑠𝑒𝑛 =
𝑜𝑝
ℎ𝑖𝑝
𝑐𝑜𝑠 =
𝑎𝑑
ℎ𝑖𝑝
𝑡𝑎𝑛 =
𝑜𝑝
𝑎𝑑
Alfabeto griego
Alpha 𝛼 Α Nu 𝜈 Ν
Beta 𝛽 Β Xi 𝜉 Ξ
Gamma 𝛾 Γ Ómicron 𝜊 Ο
Delta 𝛿 Δ Pi 𝜋 Π
Épsilon 𝜀 Ε Rho 𝜌 Ρ
Zeta 𝜁 Ζ Sigma 𝜎 Σ
Eta 𝜂 Η Tau 𝜏 Τ
Theta 𝜃 Θ Upsilon 𝜐 Υ
Lota 𝜄 Ι Phi 𝜙 Φ
Kappa 𝜅 Κ Chi 𝜒 Χ
Lambda 𝜆 Λ Psi 𝜓 Ψ
Mu 𝜇 Μ Omega 𝜔 Ω
Angulo recto ൫900
൯ Catetos ൫3 𝑦 4൯ Hipotenusa ሺ5ሻ
Identificar con colores cada elemento

4. Trigonometría del triángulo rectángulo
Página 4 de 14
4. Ahora con todos los elementos localizados (ángulo de 900
, catetos e hipotenusa) se procede a ubicar un ángulo
cualquiera theta.
ℎ𝑖𝑝𝑜𝑡𝑒𝑛𝑢𝑠𝑎 = 5 𝑎𝑑𝑦𝑎𝑐𝑒𝑛𝑡𝑒 = 4 𝑜𝑝𝑢𝑒𝑠𝑡𝑜 = 3
sen 𝜃 =
3
5
cos 𝜃 =
4
5
tan 𝜃 =
3
4
Intentémoslo con el otro ángulo, que se llamará 𝒙.
ℎ𝑖𝑝𝑜𝑡𝑒𝑛𝑢𝑠𝑎 = 5 𝑎𝑑𝑦𝑎𝑐𝑒𝑛𝑡𝑒 = 3 𝑜𝑝𝑢𝑒𝑠𝑡𝑜 = 4
sen 𝑥 =
4
5
cos 𝑥 =
3
5
tan 𝑥 =
4
3
Ejemplo 1
Selecciona un ángulo ሺ𝜃ሻ.
ℎ𝑖𝑝𝑜𝑡𝑒𝑛𝑢𝑠𝑎 = 𝑎𝑑𝑦𝑎𝑐𝑒𝑛𝑡𝑒 = 𝑜𝑝𝑢𝑒𝑠𝑡𝑜 =
𝑠𝑜ℎ 𝑐𝑎ℎ 𝑡𝑜𝑎
sen 𝜃 =
7
√65
⋅
√65
√65
=
7√65
65
cos 𝜃 =
4
√65
⋅
√65
√65
=
4√65
65
tan 𝜃 =
7
4
teorema de Pitágoras

5. Trigonometría del triángulo rectángulo
Página 5 de 14
Ejemplo 2
Selecciona un ángulo ሺ300ሻ.
ℎ𝑖𝑝𝑜𝑡𝑒𝑛𝑢𝑠𝑎 = 𝑎𝑑𝑦𝑎𝑐𝑒𝑛𝑡𝑒 = 𝑜𝑝𝑢𝑒𝑠𝑡𝑜 =
𝑠𝑜ℎ 𝑐𝑎ℎ 𝑡𝑜𝑎
sen 𝜃 =
7
√65
⋅
√65
√65
=
7√65
65
cos 𝜃 =
4
√65
⋅
√65
√65
=
4√65
65
tan 𝜃 =
7
4
Selecciona un ángulo ሺ600ሻ.
ℎ𝑖𝑝𝑜𝑡𝑒𝑛𝑢𝑠𝑎 = 𝑎𝑑𝑦𝑎𝑐𝑒𝑛𝑡𝑒 = 𝑜𝑝𝑢𝑒𝑠𝑡𝑜 =
𝑠𝑜ℎ 𝑐𝑎ℎ 𝑡𝑜𝑎
sen 𝜃 =
7
√65
⋅
√65
√65
=
7√65
65
cos 𝜃 =
4
√65
⋅
√65
√65
=
4√65
65
tan 𝜃 =
7
4
Razones trigonométricas en triángulos rectángulos
5.
6.
teorema de Pitágoras

6. Trigonometría del triángulo rectángulo
Página 6 de 14
7.
8.
Actividades
9. ℎ𝑖𝑝𝑜𝑡𝑒𝑛𝑢𝑠𝑎 = 9 y un 𝑐𝑎𝑡𝑒𝑡𝑜 = 5 y utilice ángulos ∠ = 𝛼 y ∠ = 𝛽
∠ = 𝛼 ℎ = 𝑜𝑝 = 𝑎𝑑 = ∠ = 𝛽
𝒔𝒐𝒉 𝒄𝒂𝒉 𝒕𝒐𝒂 ℎ = 9 𝑜𝑝 = 5 𝑎𝑑 = 3√7
sen 𝛼 =
√7
3
cos 𝛼 =
5
9
tan 𝛼 =
3√7
5
sen 𝛼 =
5
9
cos 𝛼 =
√7
3
tan 𝛼 =
5√7
21

7. Trigonometría del triángulo rectángulo
Página 7 de 14
10. 𝑐𝑎𝑡𝑒𝑡𝑜1 = 3 y 𝑐𝑎𝑡𝑒𝑡𝑜2 = 9 y utilice ángulos ∠ = 𝑥 y ∠ = 𝑦
∠ = 𝑥 ∠ = 𝑦
ℎ = 3√10 𝑜𝑝 = 9 𝑎𝑑 = 3 ℎ = 3√10 𝑜𝑝 = 3 𝑎𝑑 = 9
sen 𝑥 =
3√10
10
cos 𝑥 =
√10
10
tan 𝑥 = 3 sen 𝑦 =
√10
10
cos 𝑦 =
3√10
10
tan 𝑦 =
1
3
11.
∠ = 𝜔 = 630
∠ = 𝜃 = 270
ℎ = 3√5 𝑜𝑝 = 6 𝑎𝑑 = 3 ℎ = 3√10 𝑜𝑝 = 3 𝑎𝑑 = 6
sen 𝜔 =
2√5
5
cos 𝜔 =
√5
5
tan 𝜔 = 2 sen 𝜃 =
√5
5
cos 𝜃 =
2√5
5
tan 𝜃 =
1
2
12.

8. Trigonometría del triángulo rectángulo
Página 8 de 14
∠ = 𝐴 ∠ = 𝐶
ℎ = 8 𝑜𝑝 = 6 𝑎𝑑 = 2√7 ℎ = 8 𝑜𝑝 = 2√7 𝑎𝑑 = 6
sen 𝐴 =
3
4
cos 𝐴 =
√7
4
tan 𝐴 =
3√7
7
sen 𝐶 =
√7
4
cos 𝐶 =
3
4
tan 𝐶 =
√7
3
Resolver un lado en triángulos rectángulos con trigonometría
Podemos utilizar razones trigonométricas para determinar lados desconocidos en triángulos rectángulos.
EJEMPLO 1
Dado △ 𝐴𝐵𝐶, determina 𝐴𝐵̅̅̅̅.
Solución
Se observa que el ángulo 𝐶, está dado explícitamente en el gráfico.
También se observa que han dado la hipotenusa, y piden determinar la longitud
del lado opuesto al ángulo 𝐶.
∠𝐶 = 500
ℎ𝑖𝑝 = 6 𝑜𝑝 = 𝑥
La razón trigonométrica a utilizar es el seno.
sen 𝐶 =
𝑜𝑝
ℎ𝑖𝑝
Se despeja el opuesto.
𝑜𝑝 = ℎ𝑖𝑝 ⋅ sen 𝐶
Se reemplaza los valores
𝑥 = 6 sin500 𝑥 = 4.60
El lado 𝐴𝐵̅̅̅̅ = 4.60
Problemas
13. Dado △ 𝐹𝐻𝑀, determina 𝐹𝑀̅̅̅̅̅. Redondea tu respuesta a la centésima más cercana.
Declaración de variables
Á𝑛𝑔𝑢𝑙𝑜 𝐿𝑎𝑑𝑜 1 𝐿𝑎𝑑𝑜 2
∠𝐹 = 350
𝑎𝑑 = 4 ℎ𝑖𝑝 = 𝑥
Razón trigonométrica a utilizar
cos 𝐹 =
𝑎𝑑
ℎ𝑖𝑝
Variable despejada
ℎ𝑖𝑝 =
𝑎𝑑
cos 𝐹
Respuesta:

9. Trigonometría del triángulo rectángulo
Página 9 de 14
14. Dado △ 𝑄𝑃𝑇, determina 𝑄𝑇̅̅̅̅. Redondea tu respuesta a la centésima más cercana.
Declaración de variables
Á𝑛𝑔𝑢𝑙𝑜 𝐿𝑎𝑑𝑜 1 𝐿𝑎𝑑𝑜 2
∠𝐹 = 350
𝑎𝑑 = 4 ℎ𝑖𝑝 = 𝑥
Razón trigonométrica a utilizar
cos 𝐹 =
𝑎𝑑
ℎ𝑖𝑝
Variable despejada
ℎ𝑖𝑝 =
𝑎𝑑
cos 𝐹
Respuesta:
15. Dado △ 𝐻𝑀𝑁, determina 𝐻𝑀̅̅̅̅̅. Redondea tu respuesta a la centésima más cercana.
Declaración de variables
Á𝑛𝑔𝑢𝑙𝑜 𝐿𝑎𝑑𝑜 1 𝐿𝑎𝑑𝑜 2
∠𝐹 = 350
𝑎𝑑 = 4 ℎ𝑖𝑝 = 𝑥
Razón trigonométrica a utilizar
cos 𝐹 =
𝑎𝑑
ℎ𝑖𝑝
Variable despejada
ℎ𝑖𝑝 =
𝑎𝑑
cos 𝐹
Respuesta:
16. En el siguiente triángulo, ¿cuál de las siguientes ecuaciones puede utilizarse para encontrar 𝑥?
Elige todas las opciones correctas.
a) senሺ570ሻ =
6
𝑥
b) cosሺ570ሻ =
6
𝑥
c) cosሺ330ሻ =
6
𝑥
d) tanሺ330ሻ =
6
𝑥
17. Resuelva el triángulo rectángulo que se muestra a continuación. Mencione las longitudes en la décima más cercana.

10. Trigonometría del triángulo rectángulo
Página 10 de 14
Declaración de variables
Á𝑛𝑔𝑢𝑙𝑜 𝐿𝑎𝑑𝑜 1 𝐿𝑎𝑑𝑜 2 𝐿𝑎𝑑𝑜 3
∠𝐹 = 650
𝑎𝑑 = 5 𝑜𝑝 = 𝑥 ℎ𝑖𝑝 = 𝑦
1) Valor de 𝒙
Razón trigonométrica a utilizar
tan 𝐴 =
𝑜𝑝
𝑎𝑑
Variable despejada
𝑜𝑝 = 𝑎𝑑 ⋅ tan 𝐴
Respuesta:
2) Valor de 𝒚
Razón trigonométrica a utilizar
tan 𝐴 =
𝑜𝑝
𝑎𝑑
Variable despejada
𝑜𝑝 = 𝑎𝑑 ⋅ tan 𝐴
Respuesta:
3) Para el ángulo faltante ∠𝐶. Recordar que la suma de los ángulos
internos de un triángulo siempre vale 1800
. Como el valor del ángulo
recto siempre es 900
, nos queda la suma de los otros dos ángulos
agudos debe valer también 900
. Entonces para el ángulo ∠𝐶:
900
− 650
= 250
Respuesta
Lados Ángulos
𝐴𝐵̅̅̅̅ = 5 ∠𝐴 = 650
𝐵𝐶̅̅̅̅ ≈ 10.7 ∠𝐵 = 900
𝐴𝐶̅̅̅̅ ≈ 11.8 ∠𝐶 = 250
Ejercicios
18. Resolver el triángulo rectángulo. Redondea tu respuesta a la centésima más cercana.
Declaración de variables
Á𝑛𝑔𝑢𝑙𝑜 𝐿𝑎𝑑𝑜 1 𝐿𝑎𝑑𝑜 2 𝐿𝑎𝑑𝑜 3
∠𝐹 = 650
𝑎𝑑 = 5 𝑜𝑝 = 𝑥 ℎ𝑖𝑝 = 𝑦
1) Valor de 𝒙.
Razón trigonométrica a utilizar
tan 𝐴 =
𝑜𝑝
𝑎𝑑
Variable despejada
𝑜𝑝 = 𝑎𝑑 ⋅ tan 𝐴
Respuesta:

11. Trigonometría del triángulo rectángulo
Página 11 de 14
2) Valor de 𝒚.
Razón trigonométrica a utilizar
tan 𝐴 =
𝑜𝑝
𝑎𝑑
Variable despejada
𝑜𝑝 = 𝑎𝑑 ⋅ tan 𝐴
Respuesta:
3) Ángulo ∠𝐶.
900
− 250
= 650
Respuesta
19. Resolver el triángulo rectángulo. Redondea tu respuesta a la centésima más cercana.
Declaración de variables
Á𝑛𝑔𝑢𝑙𝑜 𝐿𝑎𝑑𝑜 1 𝐿𝑎𝑑𝑜 2 𝐿𝑎𝑑𝑜 3
∠𝐹 = 650
𝑎𝑑 = 5 𝑜𝑝 = 𝑥 ℎ𝑖𝑝 = 𝑦
1) Valor de 𝒙.
Razón trigonométrica a utilizar
tan 𝐴 =
𝑜𝑝
𝑎𝑑
Variable despejada
𝑜𝑝 = 𝑎𝑑 ⋅ tan 𝐴
Respuesta:
2) Valor de 𝒚.
Razón trigonométrica a utilizar
tan 𝐴 =
𝑜𝑝
𝑎𝑑
Variable despejada
𝑜𝑝 = 𝑎𝑑 ⋅ tan 𝐴
Respuesta:
3) Ángulo ∠𝐶.
900
− 250
= 650
Respuesta
20. Resolver el triángulo rectángulo. Redondea tu respuesta a la centésima más cercana.

12. Trigonometría del triángulo rectángulo
Página 12 de 14
Declaración de variables
Á𝑛𝑔𝑢𝑙𝑜 𝐿𝑎𝑑𝑜 1 𝐿𝑎𝑑𝑜 2 𝐿𝑎𝑑𝑜 3
∠𝐹 = 650
𝑎𝑑 = 5 𝑜𝑝 = 𝑥 ℎ𝑖𝑝 = 𝑦
1) Valor de 𝒙.
Razón trigonométrica a
utilizar
tan 𝐴 =
𝑜𝑝
𝑎𝑑
Variable despejada
𝑜𝑝 = 𝑎𝑑 ⋅ tan 𝐴
Respuesta:
2) Valor de 𝒚.
Razón trigonométrica a
utilizar
tan 𝐴 =
𝑜𝑝
𝑎𝑑
Variable despejada
𝑜𝑝 = 𝑎𝑑 ⋅ tan 𝐴
Respuesta:
3) Ángulo ∠𝐶.
900
− 250
= 650
Respuesta
21.
Declaración de variables
Á𝑛𝑔𝑢𝑙𝑜 𝐿𝑎𝑑𝑜 1 𝐿𝑎𝑑𝑜 2 𝐿𝑎𝑑𝑜 3
∠𝐹 = 650
𝑎𝑑 = 5 𝑜𝑝 = 𝑥 ℎ𝑖𝑝 = 𝑦
1) Valor de 𝒙.
Razón trigonométrica a
utilizar
tan 𝐴 =
𝑜𝑝
𝑎𝑑
Variable despejada
𝑜𝑝 = 𝑎𝑑 ⋅ tan 𝐴
Respuesta:
2) Valor de 𝒚.
Razón trigonométrica a
utilizar
tan 𝐴 =
𝑜𝑝
𝑎𝑑
Variable despejada
𝑜𝑝 = 𝑎𝑑 ⋅ tan 𝐴
Respuesta:
3) Ángulo ∠𝐶.
900
− 250
= 650

13. Trigonometría del triángulo rectángulo
Página 13 de 14
Respuesta
homework
resuelva los siguientes triángulos rectángulo. Redondéalas a la centésima más cercana.
1)
Lados Ángulos
ℎ𝑖𝑝 = 7 ∠𝐴 = 650
𝑥 = 6.34 ∠𝐵 = 900
𝑦 = 2.96 ∠𝐶 = 250
2)
Lados Ángulos
ℎ𝑖𝑝 = 7 ∠𝐴 = 650
𝑥 = 6.34 ∠𝐵 = 900
𝑦 = 2.96 ∠𝐶 = 250
3)
Lados Ángulos
ℎ𝑖𝑝 = 7 ∠𝐴 = 650
𝑥 = 6.34 ∠𝐵 = 900
𝑦 = 2.96 ∠𝐶 = 250

14. Trigonometría del triángulo rectángulo
Página 14 de 14
4)
Lados Ángulos
ℎ𝑖𝑝 = 7 ∠𝐴 = 650
𝑥 = 6.34 ∠𝐵 = 900
𝑦 = 2.96 ∠𝐶 = 250
5)
Lados Ángulos
ℎ𝑖𝑝 = 7 ∠𝐴 = 650
𝑥 = 6.34 ∠𝐵 = 900
𝑦 = 2.96 ∠𝐶 = 250