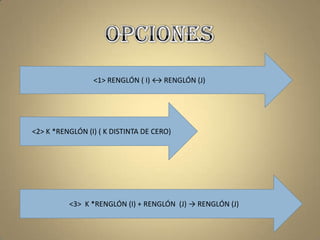
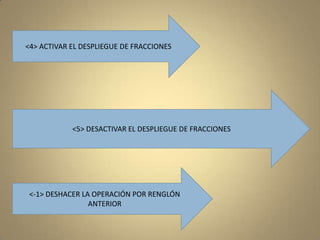
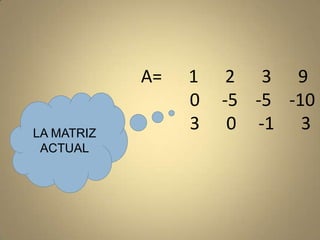
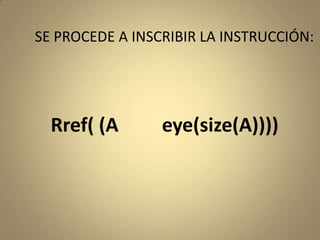
El documento describe cómo aplicar la reducción de matrices por renglones, incluyendo operaciones específicas y un ejemplo práctico. También se explica cómo calcular la inversa de matrices en Octave, mostrando el uso de la función rref y la extracción del resultado. Adicionalmente, se menciona la representación de vectores como matrices columna y el cálculo de su norma.

1. Aplicación REDUCE

2. REDUCEReduce una matriz por renglones, eligiendo de manera explícita las operaciones por renglón que deban realizarse.Una operación por renglón puede deshacerse, pero esta característica no puede utilizarse dos veces consecutivas.

3. EJEMPLO N* 1

4. **** “REDUCE” una matriz mediante la reducción por renglones**** A= 1 2 3 9 2 -1 1 8 3 0 -1 3LA MATRIZ ACTUAL ES

5. OPCIONES<1> RENGLÓN ( I) ↔ RENGLÓN (J)<2> K *RENGLÓN (I) ( K DISTINTA DE CERO) <3> K *RENGLÓN (I) + RENGLÓN (J) -> RENGLÓN (J)

6. <4> ACTIVAR EL DESPLIEGUE DE FRACCIONES <5> DESACTIVAR EL DESPLIEGUE DE FRACCIONES<-1> DESHACER LA OPERACIÓN POR RENGLÓN ANTERIOR

7. <0> SALIR DE REDUCE

8. PASO 1INTRODUZCA SU ELECCIÓN3

9. PASO 2INTRODUZCA EL FACTOR-2

10. PASO 3INTRODUZCA EL PRIMER NÚMERO DEL RENGLÓN1

11. PASO 4INTRODUZCA EL NÚMERO DE RENGLÓN POR MODIFICAR2

12. ****REEMPLAZO POR SU COMBINACION LINEALCONCLUÍDO****

13. A= 1 2 3 9 0 -5 -5 -10 3 0 -1 3LA MATRIZ ACTUAL

14. INVERSAS DE MATRICESEN OCTAVE

15. EJEMPLO 1SEA A= 1 1 1 0 2 3 5 5 1

16. SE PROCEDE A INSCRIBIR LA INSTRUCCIÓN:Rref( (A eye(size(A))))

17. Y se obtiene……..Ans= 1.0000 0 0 1.6250 -0.5000 -0.1250 0 1.0000 0 -1.8750 0.5000 0.3750 0 0 1.0000 1.2500 0 -0.2500

18. PARA EXTRAER LA MATRIZ INVERSA, HACEMOSAinv= ans(:,4:6)

19. Y obtenemos……..Ainv= 1.6250 -0.5000 -0.1250 -1.8750 0.5000 0.3750 1.2500 0 -0.2500

20. VECTORES EN OCTAVE Un n-vector X se puede representar en octave como una matriz columna con n elementos.X1 X2 O. X= (X1 X2 … Xn) X= * * *Xn

21. PARA CALCULAR SU NORMA O LONGITUDAPLICAMOS EL INSTRUCTIVOnorm(X)

22. EJEMPLO 1SEA EL VECTOR U= 2 1 1 -1

23. CALCULAR SU NORMAENTONCES:norm(u)ans.= 2.6458DESPLIEGA:

24. FinAX1=

25. HECHO PORELÍAS BADRAROSMARY BARRAGÁNAGRADECEMOS AMATLAB PARA ÁLGEBRA LINEALPROGRAMA OCTAVEPROFESOR JOSÉ GASCÓN