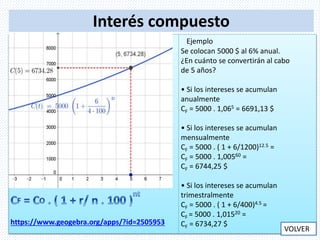
El documento describe las funciones exponenciales y sus características. Explica que una función exponencial toma la forma f(x)=bx donde b es una constante y x es la variable independiente. Las funciones exponenciales tienen aplicaciones en diversos campos como biología, economía y física. También describe cómo los parámetros de una función exponencial como el coeficiente principal y el término independiente afectan su gráfica.