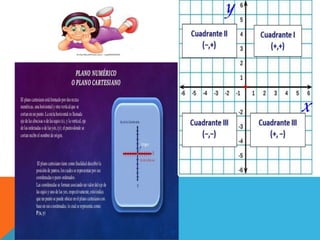
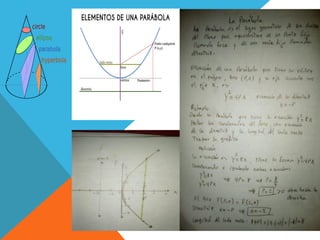
El documento define conceptos básicos de conjuntos y números reales. Explica que un conjunto está formado por elementos y puede representarse con llaves. Define la intersección de conjuntos como los elementos comunes a dos conjuntos. Luego, introduce las relaciones de orden entre números reales como desigualdades, y tipos de intervalos como abiertos, cerrados y semiabiertos.

1. REPÚBLICA BOLIVARIANA DE VENEZUELA
MINISTERIO DEL PODER POPULAR PARA LA EDUCACIÓN UNIVERSITARIA,
CIENCIA Y TECNOLOGÍA
UNIVERSIDAD POLITÉCNICA TERRITORIAL DEL ESTADO LARA
ANDRÉS ELOY BLANCO
PNF CONTADURÍA SECCIÓN 0401
U N I D A D I I : N Ú M E R O S R E A L E S Y P L A N O N U M É R I C O
Participante:
Danni Campos C.I:15.225.135
Barquisimeto, Abril 2021

2. Definición: Un conjunto es una reunión o colección de varios objetivos. Los
conjuntos en matemáticas se designa con letras mayúsculas: A,B,C,X,Y,Z
CONJUNTO:
Elementos de un Conjunto: Cada
objetivo que esta dentro del conjunto se
denomina elementos del conjunto y se
simbolizan con letras minúsculas a, b ,c, d,
etc. Un par de llaves { }, utilizado con
palabras o símbolos puede describir un
conjunto.
Ejemplo:
Dado el conjunto M formado por los dedos de una
mano.
M={pulgar, índice, medio, anular, meñique}
Los elementos de M son cada uno de los 5 dedos de
la mano: pulgar, índice, medio, anular y meñique.
Pulgar Є M se lee « El pulgar pertenece a los dedos
de la mano».
El conjunto M se puede expresar por comprensión:
M= {x / x es dedo de la mano} se lee
«El conjunto M, formado por los elementos x tales
que x es un dedo de una mano»
Sea S el conjunto de los números naturales menores que 8
S= { 1,2,3,4,5,6,7,}
S={ X/X es un numero natural menor que 8}

3. Intersección de dos Conjuntos:
Es el conjunto de todos los
elementos que se encuentran en A
y también en B. Se simboliza A ∩ B
« se lee: A intersección con B»
I. A U B={1,2,4,6,8,9,10,12,16}
II. A ∩B={4}
III. BUC={1,2,4,9,10,16}
iv. B∩C= Ø vacío

4. Relaciones de orden en el Conjunto de los Números Reales.
Desigualdades
Definición:
si a, b Є R
I. a < b ↔ b – a es positiva
II. a > b ↔ a – b es positiva
3 < 7 → 7 – 3 = 4, que es positivo
-8 < -2 → -2 – (-8) = -2+8= 6 es positivo
10 > 4 → 10 – 4 = 6 es positivo
Definición:
si a, b Є R
I. a ≤ b si y solo si a < b ò a = b
II. a ≥ b si y solo si a > b, ò bien a=b
Teorema
I. a > 0 si y solo si a es positivo
II. a < 0 si y solo si a es negativo
Teorema propiedad transitiva de orden
Si a, b, c, Є R, y
Si a> b y b> c, entonces a > c
Ejemplo:
Si x < 5 y 5 < y entonces por la
propiedad transitiva de orden se sigue
que x < y.

5. Intervalo abierto:
Es el conjunto de todas los
números x que cumplen la
desigualdad continua a < x < b
y se denota (a , b)= {x / a < x < b}
Ejemplo:
(1/2 , 4) = { x / 1/2 < x < 4 }
½
.( ) R
-1 0 1 2 3 4
Intervalo cerrado en a y b:
Es el conjunto de los números
reales comprendidos entre a y b
con la inclusión de a y b.
Se simboliza: [a , b]
[a , b ]= {x Є R / -1 ≤ x ≤ 3}
[ ]
a b
Ejemplo:
[ -1 , 3 ]= {x Є R / a ≤ x ≤ b}
[ ] R
-1 0 1 2 3

6. Intervalo semi-abierto por la izquierda
(a, b]= {x Є R / a < x ≤ b}
( ]
a b
Intervalo semi-abierto por la derecha
[ a, b)= {x Є R / a ≤ x < b}
[ )
a b