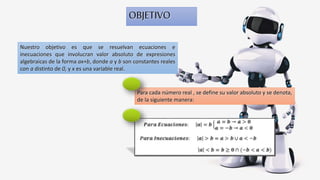
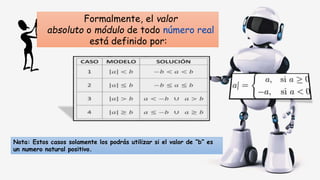
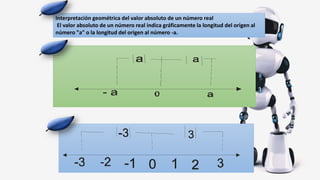
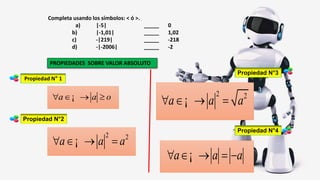
Este documento explica cómo resolver ecuaciones e inecuaciones que involucran el valor absoluto de expresiones algebraicas. Define el valor absoluto y sus propiedades, y presenta el teorema clave para resolver estas ecuaciones, que es que si a es distinto de cero, entonces la ecuación |ax + b| = c se satisface si ax + b ≥ 0 y ax + b = c o si ax + b < 0 y ax + b = -c. Proporciona un ejemplo para ilustrar cómo aplicar este teorema.

1. Ecuacionescon Valor Absoluto

3. OBJETIVO
Nuestro objetivo es que se resuelvan ecuaciones e
inecuaciones que involucran valor absoluto de expresiones
algebraicas de la forma ax+b, donde a y b son constantes reales
con a distinto de 0, y x es una variable real.
Para cada número real , se define su valor absoluto y se denota,
de la siguiente manera:

4. Valor absoluto de un número entero es el
número natural que sigue al signo. Se indica
poniendo el número entero entre barras.
El valor absoluto está relacionado con las nociones de:
Matemáticos y físicosMagnitud
Distancia

5. Formalmente, el valor
absoluto o módulo de todo número real
está definido por:
Nota: Estos casos solamente los podrás utilizar si el valor de “b” es
un numero natural positivo.

6. Interpretación geométrica del valor absoluto de un número real
El valor absoluto de un número real indica gráficamente la longitud del origen al
número "a" o la longitud del origen al número -a.

7. Completa usando los símbolos: < ó >.
a) |-5| _____ 0
b) |-1,01| _____ 1,02
c) -|219| _____ -218
d) -|-2006| _____ -2
Propiedad N° 1
PROPIEDADES SOBRE VALOR ABSOLUTO
a a o   ¡
Propiedad N°2
2 2
a a a   ¡
Propiedad N°3
2 2
a a a   ¡
Propiedad N°4
a a a    ¡

8. Propiedad N°5
, . .a b ab a b   ¡
,
aa
a b
b b
   ¡ b o
Propiedad N°6
,a b a b a b     ¡ Desigualdad
triangular
Propiedad N°6

9. Los teoremas que permiten la solución de ecuaciones con valor absoluto
son los siguientes:
 0a b b a b a b       
Ejemplos:
1.resuelve:
12 3 6x 
Desarrollo:
6 0
12 3 6 12 3 6x x     
Resolviendo las dos ecuaciones:
3 6 12 3 6 12x x      
3 6 3 18x x     
2 6x x  
 . 2;6c s 

10. Resumiendo:
Para resolver las cuaciones con valor absoluto tienes que emplear una de las
propiedades:
 0a b b a b a b       
a b a b a b    

11. BIBLIOGRAFÍA
http://www.cidse.itcr.ac.cr/cursos-linea/MATEGENERAL/t4-valorabsoluto/valor-
absoluto-julioetall/node1a.html
http://www.edutecne.utn.edu.ar/cuaterniones/Res_Ec_Inec_Modulo.pdf
Libro Matemática 1 Santillana.