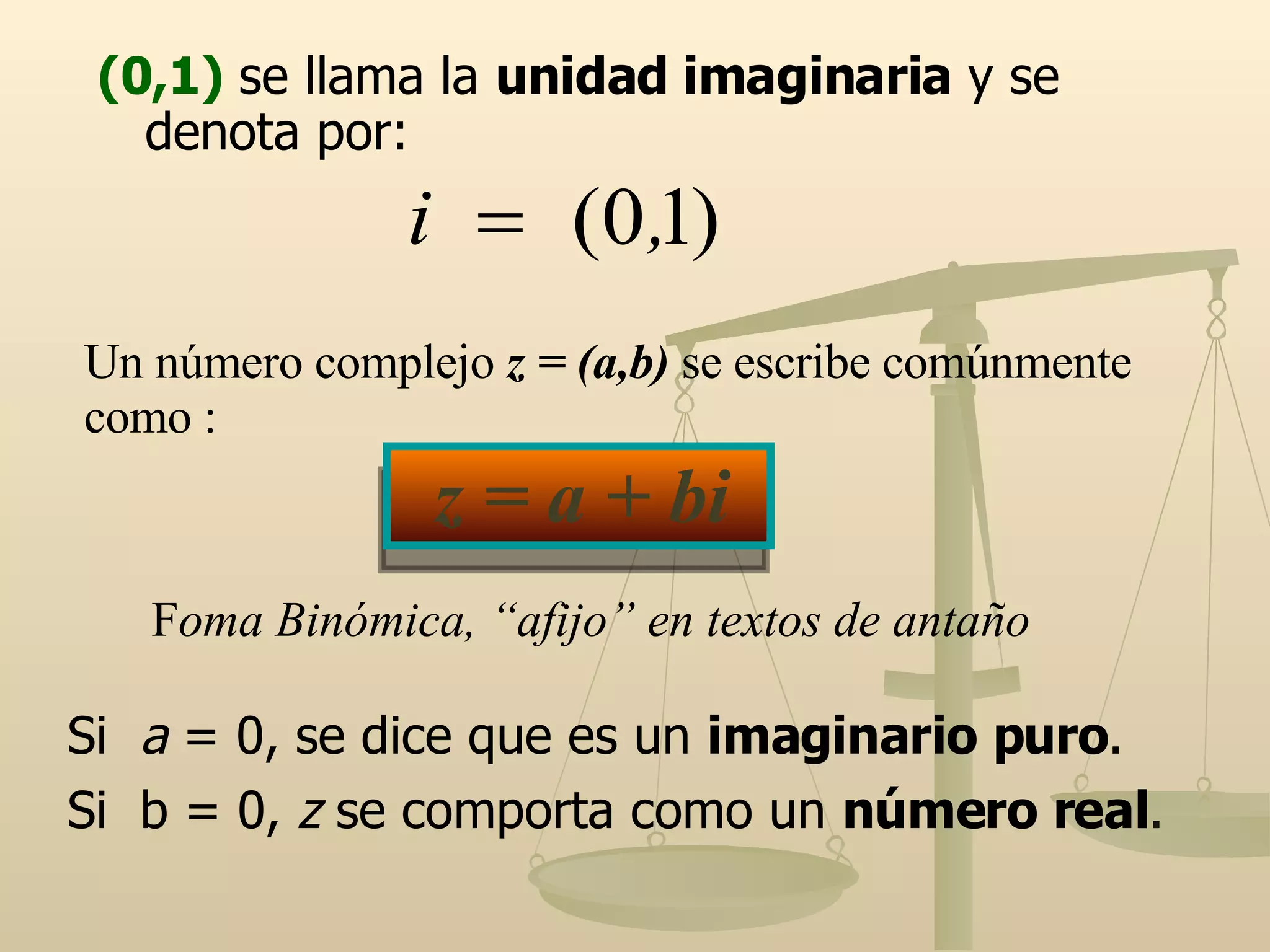
Los números complejos son pares ordenados de números reales (a, b) que pueden escribirse como z = a + bi. Esto resuelve el defecto de que los números reales no pueden solucionar ecuaciones polinómicas como x2 + 1 = 0. Un número complejo z tiene una parte real a y una parte imaginaria b. Las operaciones básicas con números complejos, como suma y diferencia, siguen reglas algebraicas similares a los números reales pero considerando sus partes real e imaginaria de forma independiente.

1. C Números Complejos PROFESOR : PUSZKO, Nicolás E. EGB 453 DNI 28.782.517 DOCENTES DISCTANTES : MOLINA, Néstor – KLIMISZYN, Diego – Stefanoff, Silvia Año : 2.008 PROGRAMA PROVINCIAL DE CAPACITACIÓN DOCENTE “ESCUELA ABIERTA” EL USO DE INTERNET COMO RECUERSO DIDÁCTICO

2. C C soluciona el defecto algebraico de R de que existan ecuaciones polinómicas con coeficientes reales que no tienen soluciones reales. Ej. x 2 + 1 = 0. Números Complejos Historia

3. Un número complejo z es un par ordenado de números reales a y b, escrito como : z = ( a,b )

4. (0,1) se llama la unidad imaginaria y se denota por: Si a = 0, se dice que es un imaginario puro . Si b = 0, z se comporta como un número real . z = a + bi Un número complejo z = (a,b) se escribe comúnmente como : F oma Binómica, “afijo” en textos de antaño

5. C z = a + bi z = ( a,b ) Representación Gráfica

6. Conjugado El conjugado de un número complejo z = x + i y se define como:

7. Opuesto El opuesto de un número complejo z = x + i y se define como:

8. Suma (Forma Binómica) Suma “ Sean : Parte real Parte imaginaria

9. Diferencia (Forma Binómica) Diferencia Sean : Parte real Parte imaginaria

10. Suma (Forma Cartesiana) Suma “ Sean : Parte real Parte imaginaria

11. Diferencia (Forma Cartesiana) Diferencia Sean : Parte real Parte imaginaria