La guía didáctica introduce los intervalos reales, definidos como el espacio entre dos números reales. Explica que hay diferentes tipos de intervalos basados en si incluyen o excluyen los extremos, y cómo representarlos gráficamente y mediante símbolos. Además, cubre operaciones básicas como unión e intersección de intervalos.

2. INTRODUCCIÓN:
Esta guía didáctica ha sido diseñada con la finalidad de afianzar los conocimientos en
relación al conjunto de números reales y las distintas operaciones que se realizan dentro
de dicho conjunto, así como también hacer énfasis en las diferentes definiciones que
tienen que ver con intervalos reales: tipos, representación grafica y operaciones.
OBJETIVO:
Definir e identificar los diferentes tipos de intervalos, y resolver ejercicios con las
operaciones básicas (Unión e intersección). A lo largo de esta guía descubrirás las
siguientes interrogantes.
¿QUÉ SE ENTIENDE POR
INTERVALO?
¿CUÁL ES LA UTILIDAD DE LOS
INTERVALOS EN LA VIDA DIARIA?
¿CUÁLES SON LOS SIMBOLOS
QUE SE UTILIZAN PARA ESCRIBIR
LOS INTERVALOS?
¿CUÁLES SON LAS OPERACIONES
BÁSICAS CON INTERVALOS?
¿CÓMO GRAFICAR LOS
DIFERENTES TIPOS DE
INTERVALOS?
¿CUÁLES SON LOS TIPOS DE
INTERVALOS?
GUÍA DIDÁCTICA: INTERVALOS REALES

3. Practicante: Heczobeth Piña
INTERVALO
Es el espacio o distancia que hay de un tiempo a otro o de un lugar a otro.
La expresión {x є R/ a<x<b} se lee: el conjunto de todos los números
reales tales que son mayores que a y menores que b.
En la recta numérica siguiente, x es un número real cualquiera que está
entre otros dos reales a y b.
____________(_________________________________________)___________
a x b
Es evidente que a<x y x<b. Esta situación se puede expresar como:
a<x<b. Como x es un número real cualquiera, la expresión a<x<b se satisface para los
infinitos valores que puede tomar x de los que existen entre a y b.
GUÍA DIDÁCTICA: INTERVALOS REALES
La expresión {x є R/ a<x<b}
representa el conjunto de
todos los números reales que
están entre otros dos reales
dados. Este conjunto de
números reales se denomina
Intervalo

4. Practicante: Heczobeth Piña
Por Ejemplo
Si se quiere hallar todos los
puntos sobre una recta real
que están entre el punto A(-
3) y el punto B(5), observa lo
que se realiza
En este caso el conjunto buscado está formado por todos los puntos
que quedan a la derecha del punto A y a la izquierda del punto B, es decir, las
coordenadas de esos puntos son mayores que -3 y son menores que 5, como se
muestra en la siguiente figura:
_________A_(_____________________________________________)_B______
-3 5
Luego, si X(x) es un punto que está entre A y B se escribe -3<x<5. A
ese conjunto de puntos se le denomina intervalo y los números -3 y 5 se llaman
sus extremos.
GUÍA DIDÁCTICA: INTERVALOS REALES

5. GUÍA DIDÁCTICA: INTERVALOS REALES
Importante:
En la figura anterior, los
extremos se han marcados con
paréntesis para indicar que no
están incluidos, es decir, que no
forman parte del conjunto. Si así
fuera se colocarían corchetes
De acuerdo con lo anterior, es posible identificar y definir en
forma analítica y en forma gráfica distintos conjuntos de
números reales en la recta real.
Dado a<b, y a, b є R, se definen los siguientes tipos de
intervalos:

6. GUÍA DIDÁCTICA: INTERVALOS REALES
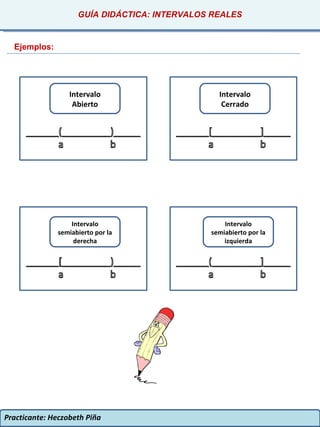
Tipos de Intervalos
Intervalo
Cerrado
Intervalo
semiabierto por la
derecha
Intervalo
semiabierto por la
izquierda
Es el conjunto de
números reales
comprendidos
entre a y b,
incluidos ambos.
Se simboliza
como:
[a,b]
Los corchetes
indican que los
extremos están
en el conjunto.
Se llama así al
conjunto de
números reales
comprendidos
entre ay b que
incluye al
extremo a, pero
no incluye al
extremo b. Se
simboliza por:
[a,b)
Se denomina
así al conjunto
de números
reales
comprendidos
entre a y b que
excluye al
extremo a,
pero incluye al
extremo b.
Se simboliza
por:
(a,b]
Intervalo
Abierto
Se denomina
así al conjunto
de números
reales
comprendidos
entre a y b. Se
simboliza por:
(a,b)
Los paréntesis
indican que los
extremos no
están en el
conjunto

7. Practicante: Heczobeth Piña
Ejemplos:
GUÍA DIDÁCTICA: INTERVALOS REALES
Intervalo
Abierto
Intervalo
Cerrado
Intervalo
semiabierto por la
derecha
Intervalo
semiabierto por la
izquierda

8. GUÍA DIDÁCTICA: INTERVALOS REALES
El conjunto de todos los números reales mayores
que un número real a, se considera un intervalo infinito de la
forma (a, +∞). El símbolo +∞ significa que el conjunto se
extiende indefinidamente a la derecha. Asimismo se pueden
definir otros intervalos infinitos, como lo son: [a,+ ∞), (- ∞,a), (-
∞,a] y (- ∞,+ ∞), en los que - ∞ significa que el conjunto se
extiende indefinidamente hacia la izquierda.
Fíjate en el siguiente ejemplo: [-2,+ ∞).
___________[_____________________________
-2 + ∞
Ahora observa cómo se halla la intersección de los intervalos
(-3,6] y [-5,4), o sea (-3,6] ∩ [-5,4). Para ello se trazan ambos
intervalos y se identifica el que contiene la parte común.
____[___(________________________)________]___
-5 -3 0 4 6
Luego, la intersección o la parte común es el intervalo (-3,4).
En otro caso, fíjate cómo se halla la unión de los intervalos (-
2,7] y (-5,4), o sea, (-2,7] U (-5,4). Esto implica determinar el
conjunto de los números reales que estén en al menos uno de
esos intervalos.
__(_______(____________________)__________]__
-5 -2 0 4 7
Al representar ambos intervalos se observa que la unión de
los conjuntos es el intervalo (-5,7]. Se colocó corchete a la
derecha porque también contiene al 7

9. GUÍA DIDÁCTICA: INTERVALOS REALES
ara hacer en el cuaderno
Representa gráficamente cada uno de los siguientes intervalos:
a)[2, 5)
b)(-∞,3]
c)(2, +∞)
d)(-4, 5]
e)[-6,1]
f)[-3, 5)
Escribe en forma de intervalo el conjunto que corresponde a
cada gráfico
a) ___[____________)___
1 12
b) _____(_____________)___
-3 0
c) ________[__________________)_____
-1 + ∞
d) _______(________________]_____
4 8

10. GUÍA DE DIDÁCTICA: INTERVALOS REALES
Curiosidades Matemáticas
Los Intervalos y el Calendario
Los Intervalos se han utilizado prácticamente
desde la existencia del hombre, quién mediante la
observación de los fenómenos naturales, comenzó a
registrar el tiempo a través de marcas en los árboles o
en su cueva.
Con el tiempo, se estableció el año de 360
días en 12 meses y 4 estaciones; pero las civilizaciones
que usaban este calendario se percataron de que este
cálculo no era exacto y tenían que agregar días para
predecir el periodo de siembra y cosecha.
Fue en 45 a. C. cuando el emperador romano
Julio César fijó la duración del año en 365 días y ordenó
que se acumularan 6 horas por año, y que cada cuatrienio
se aplicara un día más, lo cual debía llevarse a cabo en
febrero; así surgió el año bisiesto,
Aunque el cálculo de Julio César fue muy
aproximado, cometió un error, ya que al año solar no le
sobran 6 horas, sino 5 horas, 48 minutos y 46 segundos.
Esa pequeña diferencia no fue grave al principio, pero
hacia el siglo XVI ya había producido una diferencia tan
grande y un desplazamiento de las estaciones que pro
ello, en 1582, el papa astrónomo Gregorio XIII
determinó que el calendario fuera adelantado 19 días
para actualizarse. Su calendario fue más preciso: apenas
tiene un error de 1 día, 4 horas y 48 minutos en 4000
años