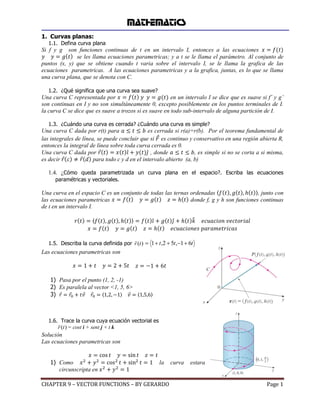
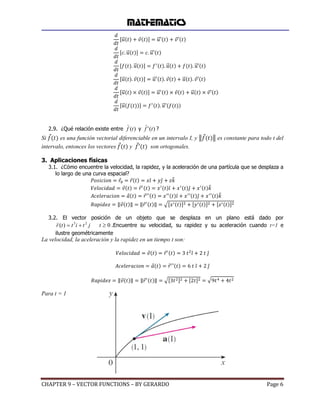
1. El documento habla sobre curvas planas y funciones vectoriales. Define conceptos como curva suave, cerrada, simple y cómo queda parametrizada una curva plana en el espacio. También explica qué es una función vectorial y su relación con curvas espaciales. 2. Describe cómo calcular la velocidad, aceleración y vector tangente de una función vectorial, así como las reglas para derivar diferentes funciones vectoriales. 3. Explica cómo encontrar la velocidad, rapidez y aceleración de una partícula que se desplaza

1. 1. Curvas planas:
1.1. Defina curva plana
MMMMAAAATTTTHHHHEEEEMMMMAAAATTTTIIIICCCCSSSS
Si f y g son funciones continuas de t en un intervalo I, entonces a las ecuaciones
se les llama ecuaciones parametricas; y
puntos (x, y) que se obtiene cuando t varia sobre el intervalo I, se le llama la grafica de las
ecuaciones parametricas. A las ecuaciones parametricas y a la grafica, juntas, es lo que se llama
una curva plana, que se denota con C.
1.2. ¿Qué significa que una curva sea suave?
Una curva C representada por
son continuas en I y no son simultáneamente 0, excepto posiblemente en los puntos terminales
la curva C se dice que es suave a trozos si es suave en todo sub
1.3. ¿Cuándo una curva es cerrada? ¿Cuándo una curva es simple?
Una curva C dada por r(t) para
las integrales de línea, se puede concluir que si
entonces la integral de línea sobre toda curva cerrada es 0.
Una curva C dada por
es decir

2. para todo c y d en el intervalo abierto (a, b)
1.4. ¿Cómo queda parametrizada un curva plana en el espacio?.
paramétricas y vectoriales.
Una curva en el espacio C es un conjunto de todas las ternas ordenadas
las ecuaciones parametricas
de t en un intervalo I.
1.5. Describa la curva definida por
Las ecuaciones parametricas son
1) Pasa por el punto (1, 2, -1)
2) Es paralela al vector 1, 5, 6
3)
1.6. Trace la curva cuya ecuación vectorial es
r (t) = cost i + sent j + t k
Solución
Las ecuaciones parametricas son
1) Como
circunscripta en
CHAPTER 9 – VECTOR FUNCTIONS
– BY GERARDO
a t se le llama el parámetro. Al conjunto de
enota en un intervalo I se dice que es suave si f’ y g’
de I.
a sub-intervalo de alguna partición de I.
es cerrada si r(a)=r(b). Por el teorema fundamental de
!
es continuo y conservativo en una región abierta R,
# $# , donde , es simple si no se corta a si
Escriba
misma,
las ecuaciones
, junto con
% donde f, g y h son funciones continuas
# $# '(

3. )

4. *+,(

5. +
*-
% (

6. )

7. *+,(./
0(
*

8. .
r (t) = 1+ t,2 + 5t,−1+ 6t
% 1
1
23 %
23 la curva estara
Page 1
(

9. +
*-