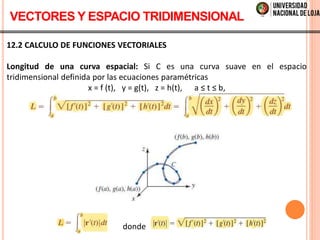
Este documento trata sobre cálculo vectorial y funciones vectoriales. Explica conceptos como funciones de valores vectoriales, rectas, curvas helicoidales, cónicas y esféricas en el espacio tridimensional. También cubre el cálculo de funciones vectoriales como límites, derivadas, integrales, longitud de curvas espaciales y movimiento sobre una curva.










![12.2 CALCULO DE FUNCIONES VECTORIALES
Interpretacion geometrica de r'(t): Como sugieren las figuras, la posición límite del
vector [r(t+h) - r(t)]/h es un vector sobre la recta tangente en P. También definimos
la recta tangente como la recta que pasa por P que es paralela al vector r'(t).
VECTORES Y ESPACIO TRIDIMENSIONAL](https://image.slidesharecdn.com/calculovectorial-parteiii-200910153122/85/Calculo-Vectorial-Parte-III-11-320.jpg)

![12.2 CALCULO DE FUNCIONES VECTORIALES
Integrales de funciones vectoriales: Si r(t) = f(t) i + g(t) j + h(t) k es una función
vectorial continua sobre el intervalo [a, b], entonces la integral indefinida de r está
definida por
Debido a la continuidad de las funciones componentes f, g y h, la integral definida
de r(t) sobre [a, b] puede definirse como
donde R es una función vectorial tal que R'(t) = r(t)
VECTORES Y ESPACIO TRIDIMENSIONAL
https://www.mathway.com/es/popular-problems/Calculus/546291
https://www.calculadora-de-derivadas.com/](https://image.slidesharecdn.com/calculovectorial-parteiii-200910153122/85/Calculo-Vectorial-Parte-III-13-320.jpg)