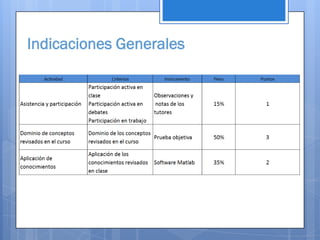
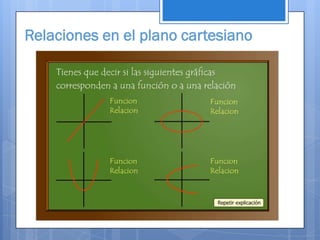
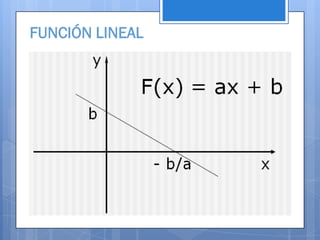
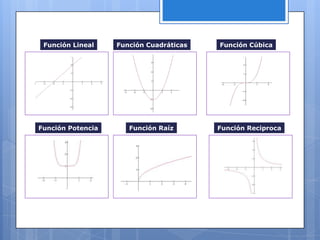
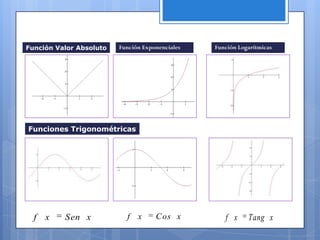
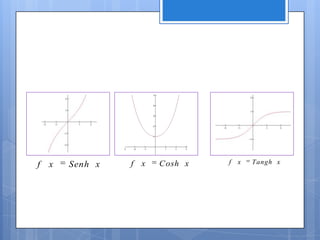
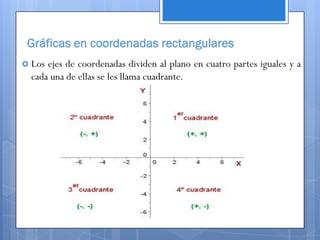
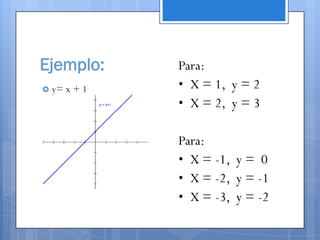
Este documento contiene información sobre diferentes temas matemáticos como sistemas de ecuaciones, funciones y gráficas. Explica métodos para resolver sistemas de ecuaciones lineales y cuadráticas como sustitución, igualación y reducción. También define conceptos de funciones como lineales, cuadráticas, trigonométricas y su combinación. Por último, describe cómo graficar funciones en coordenadas rectangulares y cómo dividir el plano cartesiano en cuadrantes.

1. Datos Personales
Andrea Katherine Iñiguez Medina
akiniguez@utpl.edu.ec
andre.iniguez@gmail.com

2. Indicaciones Generales

3. Indicaciones Generales
Aplicación de conocimientos:
 Realizar un trabajo práctico de los de los temas revisados en
clase.
 El trabajo se deberá realizar en grupos de cinco personas.
 Dibujar las funciones trigonométricas principales

4. Sistemas de ecuaciones lineales y
cuadráticas: Métodos de resolución


6. Sistemas de ecuaciones lineales y
cuadráticas: Métodos de resolución


7. Métodos de resolución
 Resolver un sistema es hallar los valores de las incógnitas que
cumplen con todas y cada una de las ecuaciones. Estos valores
se conocen como soluciones del sistema
 Sea el sistema x+y=2
x –y=0
 Como se puede apreciar por su sencillez la única solución
posible es x = 1 e y = 1, pues son los valores de las
incógnitas que hacen posible que se cumplan las dos
igualdades.

8. Reglas que permiten resolver sistemas
1. Si a los dos miembros de una ecuación de un sistema se les suma o
resta un mismo número o expresión algebraica, resulta otro sistema
equivalente al dado.
2. Si se multiplican o dividen los dos miembros de una ecuación de un
sistema por un mismo número o expresión algebraica distinto de
cero, resulta otro sistema equivalente al dado.
3. Reemplazar cualquiera de los miembros de una ecuación por una
expresión igual (equivalente)

9. Métodos de resolución
Para resolver un sistema de ecuaciones lineales existen varios métodos:
 Método de Sustitución: Es el más empleado, pues permite
resolver la mayoría de los sistemas, tanto de ecuaciones lineales como
cuadráticas, exponenciales o logarítmicas.
 Método de Igualación: Es una variante del método anterior,
utilizada muy puntualmente.
 Método de Reducción: Es muy empleado para sistemas lineales
con igualdad de coeficientes, y especialmente para sistemas
cuadráticos.

10. Método de Sustitución
Si en una ecuación de un sistema se sustituye una incógnita por la expresión que se
obtiene al despejarla de la otra ecuación, resulta otro sistema equivalente.
 Ejemplo 1
Sea el sistema: x + 3.y = 4 (1)
3.x - y = 2 (2)
 De la ecuación (1) se despeja la incógnita “x” : x = 4 – 3.y
 Y se sustituye su expresión en la ecuación (2) : 3 (4 – 3.y) – y = 2
 Operando … 12 – 9.y – y = 2  12 – 2 = 9.y + y  10 = 10.y 
y=1
 Llevando ese valor a la ecuación ( 1 ), tenemos …
x = 4 – 3.y = 4 – 3.1 = 4 – 3 = 1 , o sea x = 1

11. Método de Igualación

12. Método de Reducción
1. Buscamos que los coeficientes de una incógnita cualquiera (x o y) sean
iguales pero de signo contrario, multiplicando por los números
convenientes a una o ambas ecuaciones.
2. Restamos las ecuaciones para eliminar una de las incógnitas.
3. Resolvemos la ecuación resultante, con lo que hallamos el valor de una
de las incógnitas.
4. Sustituimos el valor obtenido en cualquiera de las ecuaciones iniciales
y resolvemos la nueva ecuación, con lo que hallamos el valor de la otra
incógnita.
5. Comprobamos la solución obtenida.

13. Ejemplo
 Sea el sistema: x + 3.y = 4 (1)
3.x - y = 2 (2)
 Multiplicamos la ecuación (1) por 3, resultando otra EQUIVALENTE, pero
teniendo el mismo coeficiente en x.
3.x + 9.y = 12 (1)
3.x - y = 2 (2)
 A la ecuación (1) la resto la (2), quedando:
y=1
 Sustituyendo el valor de “y” en la ecuación (1), tenemos:
x=1
 La solución del sistema es: x = 1 , y = 1

14. Ecuaciones cuadráticas


15. FUNCIONES MATEMÁTICAS
 Relación es la correspondencia de un primer conjunto,
llamado Dominio, con un segundo conjunto, llamado Rango,
de manera que a cada elemento del Dominio le corresponde
uno o más elemento del Recorrido o Rango.
 Una Función es una relación a la que se añade la restricción
de que a cada valor del Dominio le corresponde uno y sólo
un valor del recorrido.

16. Definición de relación y de función

17. 

18. 

19. Relaciones en el plano cartesiano

20. FUNCIÓN LINEAL

21. FUNCIÓN CUADRÁTICA

22. FUNCIONES ESPECIALES


23. 

24. Función Lineal Función Cuadráticas Función Cúbica
Función Potencia Función Raíz Función Reciproca

25. Función Valor Absoluto Función Exponenciales Función Logarítmicas
Funciones Trigonométricas
f x Sen x f x C os x f x Tang x

26. f x Senh x f x Cosh x f x Tangh x

27. Combinación de funciones
 Existen diferentes métodos para combinar dos funciones
para crear una nueva función.
Suma de f y g f g x f x g x
Resta de f y g f g x f x g x
Producto de f y g f g x f x g x
f f x
Cociente de f y g x g x 0
g g x

28. Gráficas en coordenadas rectangulares
 Los ejes de coordenadas dividen al plano en cuatro partes iguales y a
cada una de ellas se les llama cuadrante.

29. Ejemplo: Para:
 y= x + 1 • X = 1, y = 2
• X = 2, y = 3
Para:
• X = -1, y = 0
• X = -2, y = -1
• X = -3, y = -2

30. Ejemplo:

x y
1 1
2 4
3 9
0 0
-1 1
-2 2
-3 9