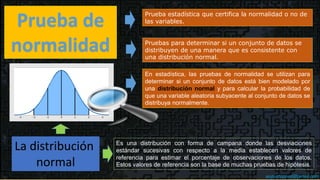
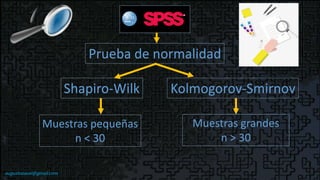
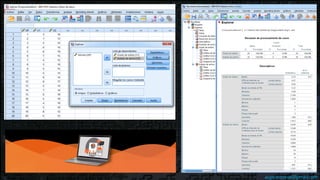
Este documento describe las pruebas de normalidad de Shapiro-Wilk y Kolmogorov-Smirnov para determinar si un conjunto de datos se distribuye normalmente. La prueba de Shapiro-Wilk se recomienda para muestras pequeñas menores a 30, mientras que la prueba de Kolmogorov-Smirnov es mejor para muestras grandes mayores a 30. El documento también explica cómo interpretar los resultados estadísticos de estas pruebas en SPSS para concluir si los datos se aproximan o no a una distribución normal.

1. Mg. Augusto Ismael Zavala Osorio
Prueba de normalidad
en SPSS

2. Prueba estadística que certifica la normalidad o no de
las variables.
Pruebas para determinar si un conjunto de datos se
distribuyen de una manera que es consistente con
una distribución normal.
Prueba de
normalidad
En estadística, las pruebas de normalidad se utilizan para
determinar si un conjunto de datos está bien modelado por
una distribución normal y para calcular la probabilidad de
que una variable aleatoria subyacente al conjunto de datos se
distribuya normalmente.
La distribución
normal
Es una distribución con forma de campana donde las desviaciones
estándar sucesivas con respecto a la media establecen valores de
referencia para estimar el porcentaje de observaciones de los datos.
Estos valores de referencia son la base de muchas pruebas de hipótesis.
augustozaval@gmail.com

3. PRUEBA
DE
NORMALIDAD
Shapiro-Wilk
Mide la fuerza del ajuste con una recta. Se usa
para contrastar la normalidad de un conjunto
de datos.
Cuanto mayor sea el valor de este estadístico
mayor desacuerdo habrá en la recta de
normalidad, por lo que se rechaza la hipótesis
nula.
Se recomienda para muestras pequeñas,
menos de 30.
Kolmogorov-
Smirnov
Es un procedimiento de “bondad de ajuste”
que permite medir el grado de concordancia
existente entre la distribución de un conjunto
de datos y una distribución teórica específica.
Su objetivo es señalar si los datos provienen de
una población que tiene la distribución teórica
especificada, es decir, contrasta si las
observaciones podrían razonablemente
proceder de la distribución especificada.
Se recomienda para muestras mayores de 30.
augustozaval@gmail.com

4. Prueba de normalidad
Shapiro-Wilk Kolmogorov-Smirnov
Muestras pequeñas
n < 30
Muestras grandes
n > 30
augustozaval@gmail.com

5. Prueba de normalidad en
Ho: Datos se aproximan a la distribución normal. (p > alfa)
H1: Datos no se aproximan a la distribución normal. (p < alfa)
Ho: (p-valor > alfa)
H1: (p-valor < alfa)
Regla general
para hipótesis
estadística
En SPSS p = Sig. Sig. = significancia o significación calculada
Sig. : nivel de significación = 0.05 (lo que está fuera del 95 % de probabilidades
Si Sig. (p-valor) > 0.05 aceptamos H0 (hipótesis nula) → distribución normal
Si Sig. (p-valor) < 0.05 rechazamos H0 (hipótesis nula) → distribución no normal.
Entonces

6. augustozaval@gmail.com

7. augustozaval@gmail.com

8. augustozaval@gmail.com

9. augustozaval@gmail.com

10. Muestra pequeña
Shapiro-Wilk
p > alfa
P > alfa
Paramétrico
Paramétrico
Dist. normal
Dist. normal
Interpretación:
Como p > alfa, entonces aceptamos la hipótesis nula
obteniendo una distribución normal. Corresponde
una prueba paramétrica, en este caso, al ser una
correlación el estadístico sería el coeficiente de
correlación R de Pearson.
augustozaval@gmail.com

11. augustozaval@gmail.com