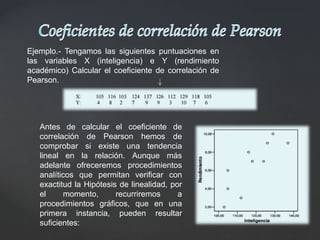
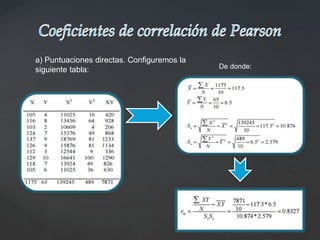
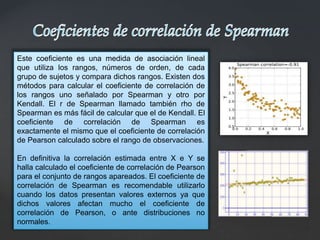
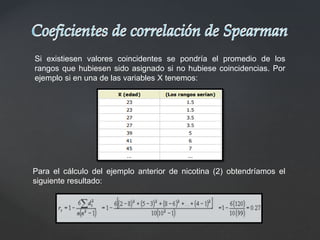
Este documento explica los coeficientes de correlación de Pearson y Spearman. El coeficiente de Pearson mide la relación lineal entre dos variables cuantitativas, variando de -1 a 1, donde 0 indica ninguna correlación y valores cercanos a 1 o -1 indican una fuerte correlación positiva o negativa. El coeficiente de Spearman es similar pero se basa en los rangos de los datos en lugar de los valores reales, haciéndolo más robusto ante valores atípicos. Ambos coeficientes son herramientas útiles para medir el grado de asociación entre

1. República Bolivariana de Venezuela
Ministerio del Poder Popular para la Educación
Superior
Instituto Universitario Politécnico “Santiago
Mariño”
Sede – Barcelona
Alumno:
Booz González.
C.I: 26.293.477
Profesor:
Pedro Beltrán
Sección CV
Barcelona, 2016

2. Los coeficientes de correlación son medidas que indican la
situación relativa de los mismos sucesos respecto a las dos
variables, es decir, son la expresión numérica que nos indica el
grado de relación existente entre las 2 variables y en qué
medida se relacionan. Son números que varían entre los límites
+1 y -1. Su magnitud indica el grado de asociación entre las
variables; el valor r = 0 indica que no existe relación entre las
variables; los valores ( 1 son indicadores de una correlación
perfecta positiva (al crecer o decrecer X, crece o decrece Y) o
negativa (Al crecer o decrecer X, decrece o crece Y).
En estadística, el coeficiente de correlación de Pearson es una
medida de la relación lineal entre dos variables aleatorias
cuantitativas. A diferencia de la covarianza, la correlación de
Pearson es independiente de la escala de medida de las
variables.
De manera menos formal, podemos definir el coeficiente de
correlación de Pearson como un índice que puede utilizarse
para medir el grado de relación de dos variables siempre y
cuando ambas sean cuantitativas.

3. En el caso de que se esté estudiando dos
variables aleatorias X y Y sobre una
población; el coeficiente de correlación de
Pearson se simboliza con la letra px,y siendo
la expresión que nos permite calcularlo:
Donde:
De manera análoga podemos
calcular este coeficiente sobre un
estadístico muestral, denotado
como rx,y a:

4. Valor del
Coeficiente de Pearson
Grado de Correlación
entre las Variables
r = 0
Ninguna correlación
r = 1 Correlación positiva perfecta
0 < r < 1 Correlación positiva
r = -1 Correlación negativa perfecta
-1 < r < 0 Correlación negativa
Nótese que una correlación negativa no es menos fuerte que una
correlación positiva. Así, por ejemplo, un de 0,5 es tan ‘grande’ o fuerte
como un de –0,5. Los signos positivos y negativos sólo indican si el valor
de una variable aumenta o disminuye, respectivamente, con el aumento
en el valor de la otra variable. Como usted sabe, cuando los aumentos
(disminuciones) de una variable producen aumentos (disminuciones) en la
otra, la relación es positiva. Es negativa cuando los aumentos
(disminuciones) de una variable producen disminuciones (aumentos) en la
otra.

5. Ventajas
 El valor del coeficiente de
correlación es independiente de
cualquier unidad usada para
medir variables
 Mientras mas grande sea la
muestra mas exacta será la
estimación
Desventajas
 El valor 0 representa falta
de correlación.
 Cuando las variables X e Y
son independientes, el
numerador se anula y el
coeficiente de correlación
poblacional tiene el valor
cero.
 En cambio una correlación
nula no implica la
independencia de variables.

6. Ejemplo.- Tengamos las siguientes puntuaciones en
las variables X (inteligencia) e Y (rendimiento
académico) Calcular el coeficiente de correlación de
Pearson.
Antes de calcular el coeficiente de
correlación de Pearson hemos de
comprobar si existe una tendencia
lineal en la relación. Aunque más
adelante ofreceremos procedimientos
analíticos que permitan verificar con
exactitud la Hipótesis de linealidad, por
el momento, recurriremos a
procedimientos gráficos, que en una
primera instancia, pueden resultar
suficientes:

7. a) Puntuaciones directas. Configuremos la
siguiente tabla: De donde:

8. Este coeficiente es una medida de asociación lineal
que utiliza los rangos, números de orden, de cada
grupo de sujetos y compara dichos rangos. Existen dos
métodos para calcular el coeficiente de correlación de
los rangos uno señalado por Spearman y otro por
Kendall. El r de Spearman llamado también rho de
Spearman es más fácil de calcular que el de Kendall. El
coeficiente de correlación de Spearman es
exactamente el mismo que el coeficiente de correlación
de Pearson calculado sobre el rango de observaciones.
En definitiva la correlación estimada entre X e Y se
halla calculado el coeficiente de correlación de Pearson
para el conjunto de rangos apareados. El coeficiente de
correlación de Spearman es recomendable utilizarlo
cuando los datos presentan valores externos ya que
dichos valores afectan mucho el coeficiente de
correlación de Pearson, o ante distribuciones no
normales.

9. El cálculo del coeficiente viene dado por:
Los valores de los rangos se colocan según el
orden numérico de los datos de la variable.
Ejemplo: Se realiza un estudio
para determinar la asociación
entre la concentración de
nicotina en sangre de un
individuo y el contenido en
nicotina de un cigarrillo (los
valores de los rangos están entre
paréntesis) (2).

10. •Se ordenan todos los casos para cada
una de las variables de interés y se les
asigna un rango consecutivo.
•Si la asociación entre ambas variables
fuera perfecta se esperaría que el rango
de ambas variables fuera exactamente
igual.
•El coeficiente de correlación se calcula
en base a las diferencias registradas en
los rangos entre ambas variables.
•Para evitar que las diferencias positivas
anulen a las negativas, el estadístico se
calcula en función de las diferencias
elevadas al cuadrado.
METODOLOGÍA

11. Si existiesen valores coincidentes se pondría el promedio de los
rangos que hubiesen sido asignado si no hubiese coincidencias. Por
ejemplo si en una de las variables X tenemos:
Para el cálculo del ejemplo anterior de nicotina (2) obtendríamos el
siguiente resultado:

12. VENTAJAS
• No se asume una relación lineal
entre las variables.
• No se asume una distribución
normal bivariada.
• Es válido para muestras en las que
no se pueden hacer medidas pero
sí asignar rangos.
• Es más robusto
INCONVENIENTES
• Pérdida de información
• La eficiencia es del 91%
(para distribuciones
normales, en el test de
Fisher basta con un tamaño
muestral un 91% menor
para rechazar la hipótesis
nula con el mismo nivel de
significación) V

13.  https://es.wikipedia.org/wiki/Coeficiente_de_correlaci%C3%B3n_de_Pearson
 http://www.lapaginadelprofe.cl/UAconcagua/ICanalisisdatoscuantitativos.htm
 http://kovachi.sel.inf.uc3m.es/@api/deki/files/141/=correlacion.pdf
 http://www.monografias.com/trabajos93/muestreo-correlaciones-
contingencias-y-pearson/muestreo-correlaciones-contingencias-y-
pearson2.shtml
 https://es.scribd.com/doc/134574744/COEFICIENTE-DE-CORRELACION-
DE-PEARSON-Y-SPEARMAN-DR-ENRIQUE-SIERRA