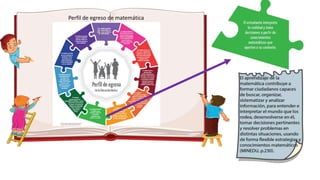
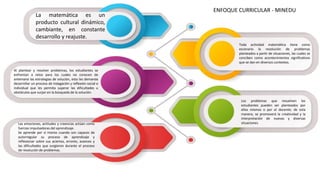
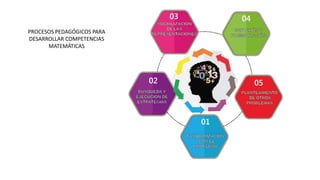
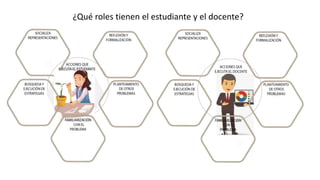
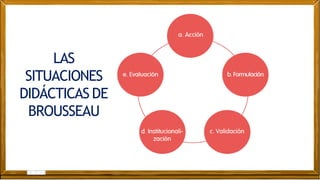
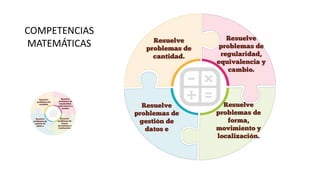
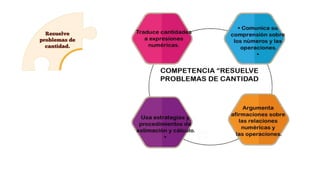
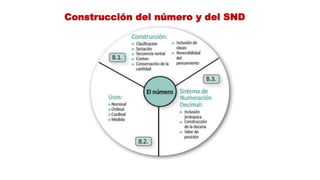
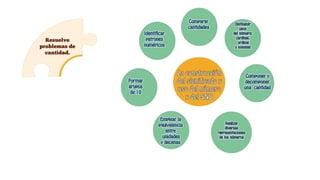
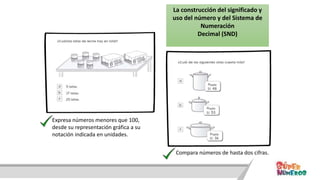
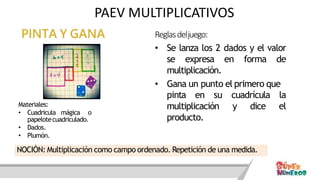
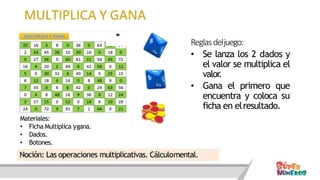
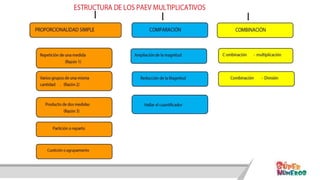
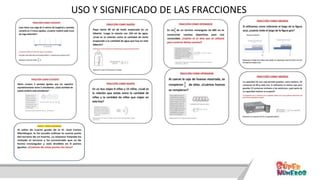
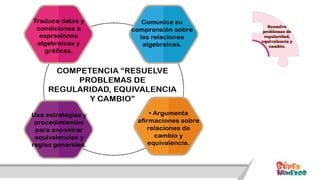
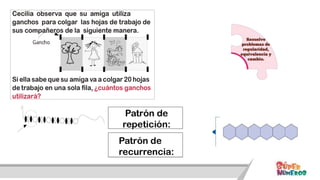
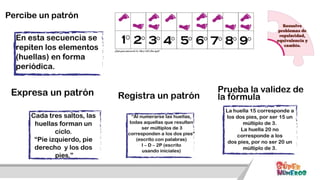
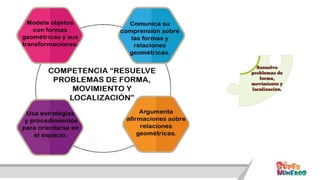
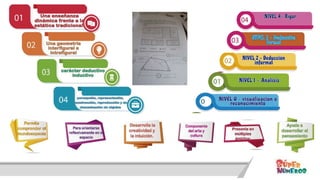
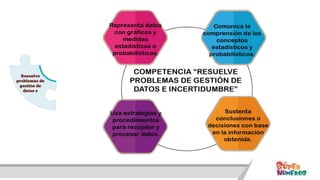
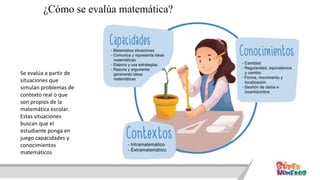
Este documento presenta información sobre las competencias matemáticas y cómo desarrollarlas. En particular, describe que las competencias matemáticas se desarrollan resolviendo problemas planteados en diversos contextos y que requieren procesos de indagación. También señala que tanto los estudiantes como los docentes juegan un rol importante en este proceso, y presenta algunas estrategias pedagógicas como las situaciones didácticas de Brousseau.

1. “La Matemática es el telar en el que Dios tejió la
tela del universo”.
Galileo
LAS COMPETENCIAS MATEMÁTICAS
MAG. FROY FRANCISCO CASTRO VENTURA

2. ANÁLISIS DE
CASO
¿Qué estudiante o estudiantes
resolvieron correctamente la
tarea planteada? ¿Por qué?

3. ¿Qué es la competencia matemática?
¿Cómo desarrollamos la competencia
matemática?

4. Perfil de egreso de matemática

5. La matemática es un
producto cultural dinámico,
cambiante, en constante
desarrollo y reajuste.
Toda actividad matemática tiene como
escenario la resolución de problemas
planteados a partir de situaciones, las cuales se
conciben como acontecimientos significativos
que se dan en diversos contextos.
Al plantear y resolver problemas, los estudiantes se
enfrentan a retos para los cuales no conocen de
antemano las estrategias de solución, esto les demanda
desarrollar un proceso de indagación y reflexión social e
individual que les permita superar las dificultades u
obstáculos que surjan en la búsqueda de la solución.
Los problemas que resuelven los
estudiantes pueden ser planteados por
ellos mismos o por el docente; de esta
manera, se promoverá la creatividad y la
interpretación de nuevas y diversas
situaciones.Las emociones, actitudes y creencias actúan como
fuerzas impulsadoras del aprendizaje.
Se aprende por sí mismo cuando son capaces de
autorregular su proceso de aprendizaje y
reflexionar sobre sus aciertos, errores, avances y
las dificultades que surgieron durante el proceso
de resolución de problemas.
ENFOQUE CURRICULAR - MINEDU

6. PROCESOS PEDAGÓGICOS PARA
DESARROLLAR COMPETENCIAS
MATEMÁTICAS

7. ¿Qué roles tienen el estudiante y el docente?

8. MARCO DE REFERENCIA
El razonamiento lógico matemático no existe por sí mismo en la
realidad, sino que este se da dentro del individuo. Cada sujeto lo
construye en su mente a través de la interacción con los objetos
(vivenciación, manipulación, representación gráfico simbólica y
abstracción reflexiva o mental)
TEORÍA COGNITIVA
“El conocimiento no puede ser una copia,
ya que siempre es una relación entre
sujeto y objeto”
Jean Piaget (1896-1980)

9. Teoría de la Situación
Didáctica
Un marco para pensar y actuar la
enseñanza de la matemática.
Guy Brousseau
Una situación didáctica es el conjunto de relaciones
establecidas explícita o implícitamente entre el
estudiante, un cierto medio –otros estudiantes,
eventualmente instrumentos u otros objetos– y un
profesor.
¿Con qué fin?
Con el fin de que dichos estudiantes se apropien de un
saber constituido o en vías de construcción.
De esto se deduce que, el escenario de la situación
didáctica es la sala de clases con sus diversos actores.
(1936-2004)

10. DIDÁCTICA DELA MATEMÁTICA
LAS
SITUACIONES
DIDÁCTICAS DE
BROUSSEAU

11. COMPETENCIAS
MATEMÁTICAS

14. Construcción del número y del SND

16. PAEV ADITIVOS

20. Resuelve situaciones de
distintos significados
aditivos presentadas en
diferentes tipos de
textos.
Resuelve problemas de varias etapas, que
requieren establecer relaciones, seleccionar
datos útiles o integrar algunos datos.
La construcción del
significado y uso
de las operaciones

21. La construcción del significado y
uso del número y del Sistema de
Numeración
Decimal (SND)
Expresa números menores que 100,
desde su representación gráfica a su
notación indicada en unidades.
Compara números de hasta dos cifras.
Identifica patrones y completa términos en secuencias numéricas.

22. Reglasdeljuego:
• Se lanza los 2 dados y el valor
se expresa en forma de
multiplicación.
• Gana un punto el primero que
cuadrícula la
y dice el
pinta en su
multiplicación
producto.
NOCIÓN: Multiplicación como campo ordenado. Repetición de una medida.
Materiales:
• Cuadricula mágica o
papelotecuadriculado.
• Dados.
• Plumón.
PAEV MULTIPLICATIVOS

23. Reglasdeljuego:
• Se lanza los 2 dados y
el valor se multiplica el
valor.
• Gana el primero que
encuentra y coloca su
ficha en elresultado.
Noción: Las operaciones multiplicativas. Cálculomental.
Materiales:
• Ficha Multiplica ygana.
• Dados.
• Botones.

25. El Reparto de los panes
“El calculador, de nombre Beremiz, y su amigo Bagdalí encontraron caído en el camino a un
pobre viajero quien resultó ser un jeque, es decir, uno de los más ricos de Bagdad. Éste había
sido atacado por una turba de persas, nómadas del desierto. Beremiz y su amigo lo
atendieron y lo invitaron a comer con los panes que ellos llevaban. Beremiz aportó 5 panes y
su amigo 3. Fueron, entonces, 8 panes los que se comieron entre los tres. Cada pan que
sacaban se lo repartían entre los 3. Mientras comían, el rico les prometió que al llegar a
Bagdad pagaría con 8 monedas de oro por los 8 panes que ellos dispusieron para alimentarse.
Y así lo hizo. Sacó las 8 monedas de oro y las repartió: – Beremiz, por tus 5 panes te daré 5
monedas. Y a ti, bagdalí, te daré por tus 3 panes 3 monedas –Cuando terminó de hablar el
jeque, inmediatamente Beremiz manifestó su desacuerdo con la repartición de las monedas:
– ¡Perdón, oh jeque! La división hecha de ese modo será muy sencilla, mas no es
matemáticamente exacta. El jeque, sorprendido, interrogó al hombre que calculaba: – ¿Por
qué la división tiene que ser de esa forma?...”
Extraído del libro “El hombre que calculaba”
DIDÁCTICA DE LAS FRACCIONES

26. USO Y SIGNIFICADO DE LAS FRACCIONES

39. ¿Cómo se evalúa matemática?
Se evalúa a partir de
situaciones que
simulan problemas de
contexto real o que
son propios de la
matemática escolar.
Estas situaciones
buscan que el
estudiante ponga en
juego capacidades y
conocimientos
matemáticos