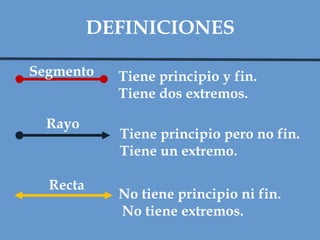
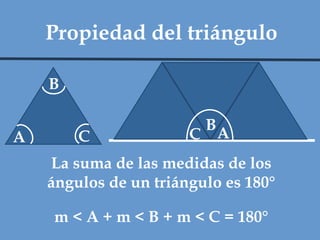
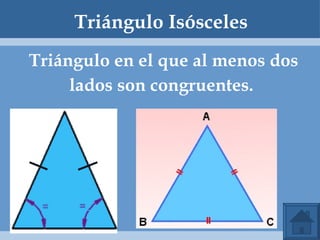
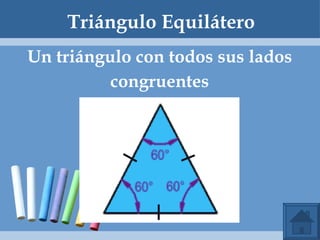
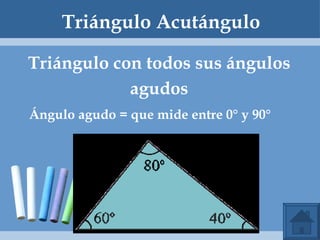
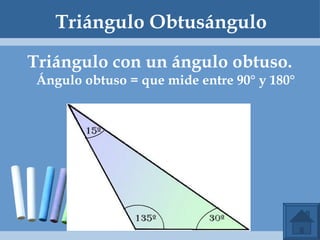
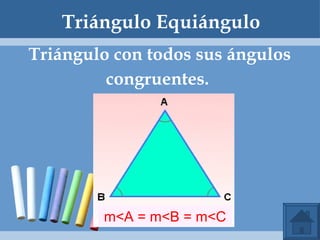
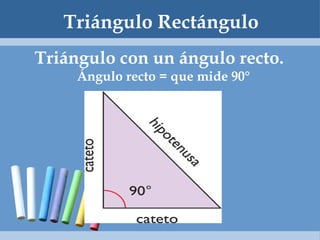
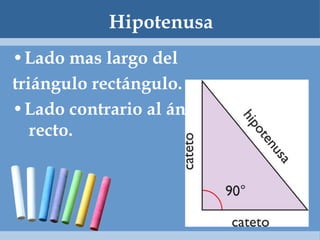
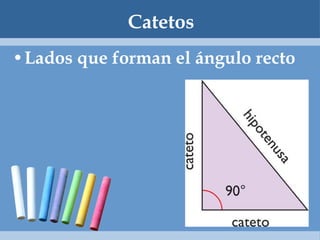
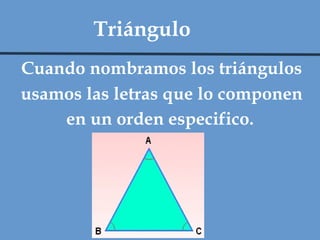
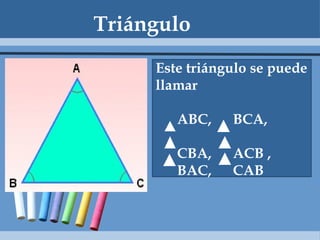
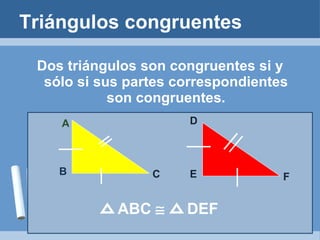
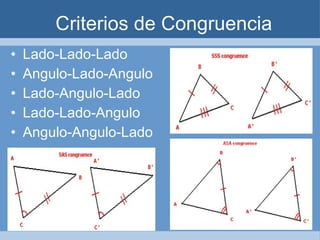
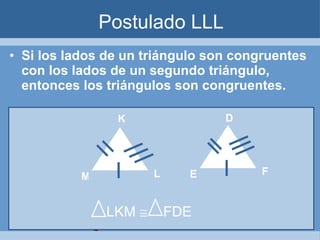
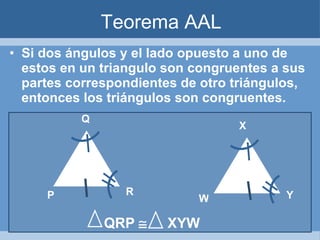
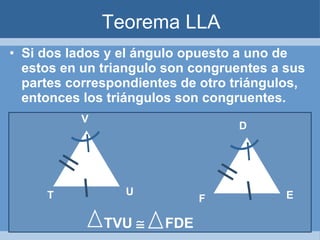
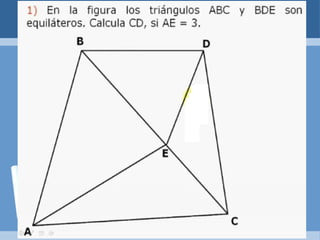
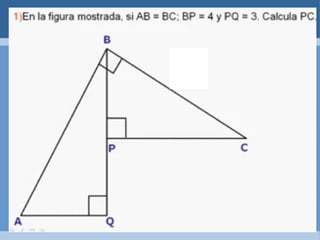
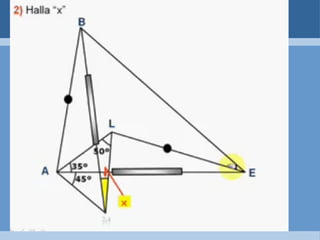
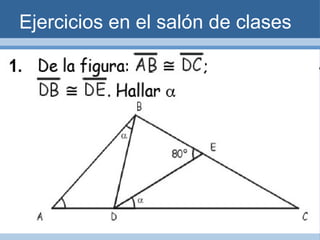
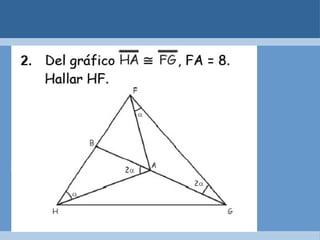
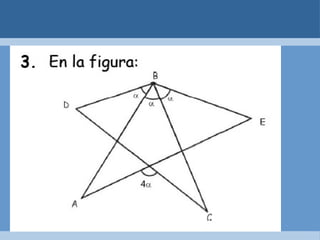
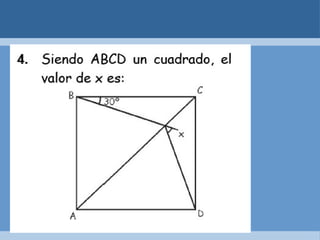
Este documento define y clasifica los triángulos. Explica que un triángulo tiene tres vértices y tres lados. Clasifica los triángulos por la longitud de sus lados (escaleno, isósceles, equilátero) y por la medida de sus ángulos (agudo, obtuso, rectángulo, equiángulo). También describe los criterios para determinar si dos triángulos son congruentes, como el postulado de lado-lado-lado.

1. TRIANGULOS

2. Segmento Rayo Recta Tiene principio y fin. Tiene dos extremos. Tiene principio pero no fin. Tiene un extremo. No tiene principio ni fin. No tiene extremos. DEFINICIONES

3. ÁNGULOS Ángulo es la unión de dos rayos. Donde se unen se conoce como el vértice del ángulo.

4. ÁNGULOS Para nombrar un ángulo hay un orden a seguir. Se utilizan tres letras donde la segunda letra debe ser el vértice del ángulo, un numero o solo el vértice El ángulo se nombra < BOA < AOB <A < 1 1

5. Las figuras geométricas componen nuestro alrededor. Una de las figuras más importante es el triángulo, el cual tendremos bajo estudio. Un triángulo es un polígono de tres lados (segmentos) o tres puntos no alineados llamados vértices.

7. Propiedad del triángulo A C B C B A La suma de las medidas de los ángulos de un triángulo es 180° m < A + m < B + m < C = 180°

8. Clasificación de triángulo Los triángulos se clasifican de acuerdo a la medida de los ángulos o de los lados. LADOS ANGULOS Escaleno Isósceles Equilátero Acutángulo Obtusángulo Equiángulo Rectángulo

9. Clasificación de triángulo Los triángulos se clasifican de acuerdo a la medida de los ángulos o de los lados. LADOS ANGULOS Escaleno Isósceles Equilátero Acutángulo Obtusángulo Equiángulo Rectángulo

10. Triángulo Escaleno Un triángulo con todos los lados de diferentes longitudes.

11. Triángulo Isósceles Triángulo en el que al menos dos lados son congruentes.

12. Triángulo Equilátero Un triángulo con todos sus lados congruentes

13. Triángulo Acutángulo Triángulo con todos sus ángulos agudos Ángulo agudo = que mide entre 0° y 90°

14. Triángulo Obtusángulo Triángulo con un ángulo obtuso. Ángulo obtuso = que mide entre 90° y 180°

15. Triángulo Equiángulo Triángulo con todos sus ángulos congruentes. m<A = m<B = m<C

16. Triángulo Rectángulo Triángulo con un ángulo recto. Ángulo recto = que mide 90°

17. Hipotenusa Lado mas largo del triángulo rectángulo. Lado contrario al ángulo recto.

18. Catetos Lados que forman el ángulo recto

19. Cuando nombramos los triángulos usamos las letras que lo componen en un orden especifico. Triángulo

20. Triángulo Este triángulo se puede llamar ABC, BCA, CBA, ACB , BAC, CAB

21. SIMBOLOS Triángulo < Ángulo = Congruente

22. Triángulos congruentes Dos triángulos son congruentes si y sólo si sus partes correspondientes son congruentes. A B C D E F ABC  DEF

23. Criterios de Congruencia Lado-Lado-Lado Angulo-Lado-Angulo Lado-Angulo-Lado Lado-Lado-Angulo Angulo-Angulo-Lado

24. Postulado LAL Si dos lados y el ángulo incluido de un triángulo son congruentes a dos lados y el ángulo incluido de otro triángulo, entonces los dos triángulos son congruentes . A B C D E ABC  FED F

25. Postulado ALA Si dos ángulos y el lado incluido de un triángulo son congruentes con dos ángulos y el lado incluido de otro triángulo, los triángulos son congruentes. A B C D E ABC  EDC

26. Postulado LLL Si los lados de un triángulo son congruentes con los lados de un segundo triángulo, entonces los triángulos son congruentes. D E F LKM  FDE M L K

27. Teorema AAL Si dos ángulos y el lado opuesto a uno de estos en un triangulo son congruentes a sus partes correspondientes de otro triángulos, entonces los triángulos son congruentes. QRP  XYW Q P R X W Y

28. Teorema LLA Si dos lados y el ángulo opuesto a uno de estos en un triangulo son congruentes a sus partes correspondientes de otro triángulos, entonces los triángulos son congruentes. TVU  FDE V T U D F E

32. Ejercicios en el salón de clases