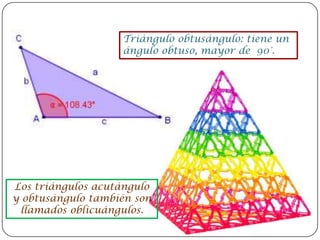
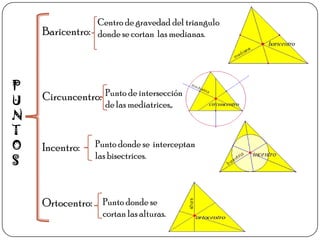
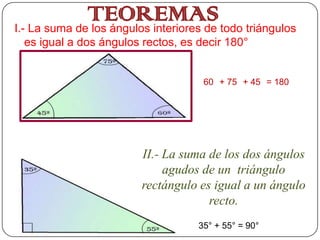
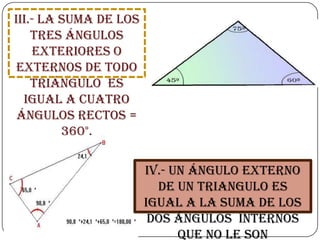
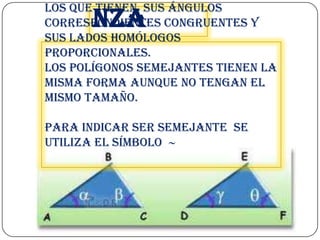
El documento proporciona información sobre triángulos. Define un triángulo como una figura plana de tres lados y tres ángulos. Explica cómo clasificar triángulos según sus lados y ángulos, y describe propiedades importantes como la suma de los ángulos internos, teoremas de congruencia y semejanza, y el teorema de Pitágoras.

1. EL TRIÁNGULO

2.  Un triángulo es una superficie plana trilateral:
> Tres ángulos
> Tres lados
> Tres vértices
Es el polígono con menos lados.
Símbolo: 1 triángulo; s triángulos
Para nombrarlo se usan tres letras en sus vértices o
una cifra romana en su interior.
Se emplean letras minúsculas para designar los lados.

3. CLASIFICACION DE LOS TRIÁNGULOS
 SEGÚN SUS LADOS:
Triángulo
Todos sus lados
a
son desiguales.
b
a ≠ b≠ c
c
El signo ≠ se lee
“diferente de ”

4. triángulo Tiene dos lados iguales
b a
a = b
c
Tiene: triángulo
B
-tres lados iguales
-ángulos iguales, siempre miden
60°.
A C
También se llama acutángulo.

5.  SEGÚN SUS ÁNGULOS
Triángulo rectángulo:
Tiene un ángulo recto .
El lado opuesto a este es la
hipotenusa.
Los lados perpendiculares
reciben el nombre de catetos.
Triángulo acutángulo:
tiene los tres ángulos
agudos, menores de 90°.

6. Triángulo obtusángulo: tiene un
ángulo obtuso, mayor de 90°.
Los triángulos acutángulo
y obtusángulo también son
llamados oblicuángulos.

7. Rectas y puntos notables del triangulo
*De cada una de estas rectas son tres en cualquier triángulo.
Segmento trazado desde un vértice
Mediana: hasta el punto medio del lado opuesto.
R
E Perpendicular trazada en el
Mediatriz: punto medio del lado opuesto.
C
T
A Recta que parte del vértice de un
Bisectriz: ángulo dividiendo a este en dos
S
exactamente iguales.
Perpendicular trazada desde
Altura: un vértice al lado apuesto
o su prolongación.

8. Centro de gravedad del triangulo
Baricentro: donde se cortan las medianas.
P
U Circuncentro: Punto de intersección
de las mediatrices,.
N
T
O Incentro: Punto donde se interceptan
las bisectrices.
S
Ortocentro: Punto donde se
cortan las alturas.

9. Propiedades de los triángulos
1.- La altura correspondiente a la base
de un triangulo isósceles es también
la mediana, mediatriz y bisectriz.
2.- En dos triángulos congruentes, a
ángulos congruentes se oponen
lados congruentes y viceversa. Estos
lados y ángulos se llaman
homólogos.
3.- Un lado es menor que la suma de
los otros dos y mayor que su
diferencia.
4.- A mayor lado se opone mayor

10. TEOREMAS todo triángulos
I.- La suma de los ángulos interiores de
es igual a dos ángulos rectos, es decir 180°
60 + 75 + 45 = 180
II.- La suma de los dos ángulos
agudos de un triángulo
rectángulo es igual a un ángulo
recto.
35° + 55° = 90°

11. III.- La suma de los
tres ángulos
exteriores o
externos de todo
triángulo es
igual a cuatro
ángulos rectos =
360°.
IV.- Un ángulo externo
de un triangulo es
igual a la suma de los
dos ángulos internos
que no le son

12. CONGRUEN
CIA
LOS TRIANGULOS SON
CONGRUETNES CUANDO TIENEN
IGUAL FORMA Y TAMAÑO. SUS
ANGULOS Y LADOS
CORRESPONDIENTES SON IGUALES.
EL SIMBOLO  SE LEE
“CONGRUENTE”

13. CASOS DE CONGRUENCIA:
1.- LAL  LAL (lado, ángulo,
lado): si un triángulo tiene dos
lados y el ángulo comprendido
congruentes a los elementos
correspondientes de otro entonces
los dos triángulos son congruentes.
2.- ALA  ALA (ángulo, lado,
ángulo): dos triángulos con dos
ángulos congruentes adyacentes
a un lado congruente, son
congruentes.

14. 2.- LLL  LLL (lado, lado, lado): si dos
triángulos tienen sus tres lados
respectivamente congruentes, entonces son
congruentes.

15.  La razón de un numero a otro es el cociente
indicado del primero entre el segundo.
La razón de 3 a 5 es 3
5
El numerador de la razón
es el antecedente y el La igualdad de dos razones
denominador es el es una proporción:
consecuente:
La proporción se escribe
a c
En la razón 3
b =d ;
4 o a : b = c : d, se lee: a es b,
3 Es el antecedente y el 4 como c es a d
el consecuente.

16. Propiedades de las
proporciones
1. En toda proporción el producto de los medios es igual al
producto de los extremos.
2. Una proporción se puede transformar en otra invirtiendo los
términos de cada razón.
3. En toda proporción un extremo cualquiera es igual al
producto de los medios entre el extremo conocido.
4. En toda proporción un medio es igual al producto de los
extremos entre el medio conocido.
5. La media proporcional, aplicando el principio 4, será igual a
la raíz cuadrada del producto de los extremos.

17. I. Si una recta es paralela a uno de los lados de un
triangulo, entonces los otros dos lados quedan divididos
en segmentos proporcionales.
II. Dos transversales cualesquiera cortadas por tres o mas
paralelas quedan divididas en segmentos proporcionales.
III. La bisectriz de un ángulo de un triángulo divide al lado
en dos segmentos proporcionales a los lados adyacentes
a ese ángulo .

18. los que tienen sus ángulos
NZA
correspondientes congruentes y
sus lados homólogos
proporcionales.
Los polígonos semejantes tienen la
misma forma aunque no tengan el
mismo tamaño.
Para indicar ser semejante se
utiliza el símbolo 

19. Razón de semejanza
Es la razón de los dos lados
homólogos.
Teorema básico de la
proporcionalidad: Casos de semejanza:
“toda recta paralela a uno de Dos triángulos son semejantes
los lados de un triangulo, •si tienen dos ángulos
determina un triangulo respectivamente congruentes.
semejante al dado.” •si tienen dos lados
proporcionales y congruente el
ángulo comprendido.
•Si tienen sus tres lados
proporcionales.

20. TEOREMA DE PITÁGORAS
EL CUADRADO CONSTRUIDO
SOBRE LA HIPOTENUSA DE UN
TRIÁNGULO RECTÁNGULO ES
IGUAL A LA SUMA DE LOS
CUADRADOS CONSTRUIDOS
SOBRE LOS CATETOS.