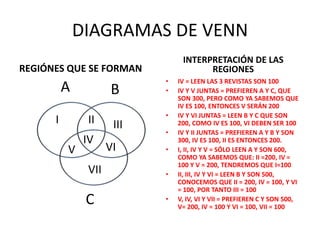
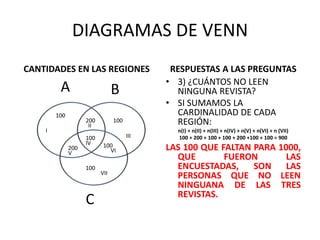
El documento presenta los resultados de una encuesta realizada a 1000 personas sobre sus preferencias por 3 revistas (A, B, C). Utiliza diagramas de Venn para resolver preguntas como cuántos leen 2 revistas, 1 revista o ninguna. Explica cómo determinar las cantidades en cada región del diagrama para encontrar las respuestas.

1. ÁLGEBRA BÁSICA
PRIMER SEMESTRE

2. 1.2 DIAGRAMA DE VENN
• UNA DE LAS MÁS IMPORTANTES ES QUE NOS
PERMITEN RESOLVER PROBLEMAS DONDE SE
INVOLUCREN VARIOS CONJUNTOS.
SUPONGAMOS QUE UNA EDITORIAL HACE UNA
ENCUESTA DE PREFERENCIAS SOBRE SUS TRES
REVISTAS A LAS QUE LLAMAREMOS A, B , C.
LOS RESULTADOS DE LA ENCUESTA REVELARON
LOS SIGUIENTES DATOS:

3. RESULTADOS DE LA ENCUESTA
• SE ENCUESTARON 1000
PERSONAS.
• 600 LEEN LA REVISTA A
• 500 LA REVISTA B
• 500 LA REVISTA C
• 200 LAS REVISTAS B Y C
• 300 LA C Y LA A
• 300 LA A Y LA B
• 100 LA A, LA B Y LA C.
• VAMOS A RESOLVER CON
LA AYUDA DE DIAGRAMAS
DE VENN LAS SIGUIENTES
PREGUNTAS:
• 1) ¿CUÁNTOS LEEN DOS Y
SÓLO DOS REVISTAS?
• 2) ¿CUÁNTOS LEEN SÓLO
UNA REVISTA?
• 3) ¿CUÁNTOS NO LEEN
NINGUNA REVISTA?

4. DIAGRAMAS DE VENN
REGIÓNES QUE SE FORMAN
INTERPRETACIÓN DE LAS
REGIONES
• IV = LEEN LAS 3 REVISTAS SON 100
• IV Y V JUNTAS = PREFIEREN A Y C, QUE
SON 300, PERO COMO YA SABEMOS QUE
IV ES 100, ENTONCES V SERÁN 200
• IV Y VI JUNTAS = LEEN B Y C QUE SON
200, COMO IV ES 100, VI DEBEN SER 100
• IV Y II JUNTAS = PREFIEREN A Y B Y SON
300, IV ES 100, II ES ENTONCES 200.
• I, II, IV Y V = SÓLO LEEN A Y SON 600,
COMO YA SABEMOS QUE: II =200, IV =
100 Y V = 200, TENDREMOS QUE I=100
• II, III, IV Y VI = LEEN B Y SON 500,
CONOCEMOS QUE II = 200, IV = 100, Y VI
= 100, POR TANTO III = 100
• V, IV, VI Y VII = PREFIEREN C Y SON 500,
V= 200, IV = 100 Y VI = 100, VII = 100
A B
I II
IV
VII
C
III
V VI

5. DIAGRAMAS DE VENN
CANTIDADES EN LAS REGIONES RESPUESTAS A LAS PREGUNTAS
• 3) ¿CUÁNTOS NO LEEN
NINGUNA REVISTA?
• SI SUMAMOS LA
CARDINALIDAD DE CADA
REGIÓN:
n(I) + n(II) + n(III) + n(IV) + n(V) + n(VI) + n (VII)
100 + 200 + 100 + 100 + 200 +100 + 100 = 900
LAS 100 QUE FALTAN PARA 1000,
QUE FUERON LAS
ENCUESTADAS, SON LAS
PERSONAS QUE NO LEEN
NINGUANA DE LAS TRES
REVISTAS.
A B
100
200 100
C
100
200 100
100
I
II
IV
III
V VI
VII

6. BUSCANDO LAS DEMÁS RESPUESTAS
• 1) ¿CUÁNTOS LEEN DOS Y SÓLO DOS REVISTAS?
SON LOS QUE ESTAN EN LAS REGIONES II, V Y VI, ASÍ QUE
SUMANDO SUS CARDINALIDADES TENEMOS:
n(II) + n(V) + n(VI) = 200 + 200 + 100 = 500
• 2) ¿CÚANTOS LEEN SÓLO UNA REVISTA?
LOS QUE ESTAN EN LAS REGIONES I, III Y VII
n(I) + n(III) + n(VII) = 100 + 100 + 100 = 300
• ¿QUÉ CANTIDAD DE LECTORES COMPRAN LAS TRES REVISTAS?
LOS QUE ESTAN EN LA ZONA IV
n(IV) = 100

7. EJERCICIO DE TAREA
EN UNA SECUNDARIA CON 300 ALUMNOS, SE PRACTICAN
FUTBOL (F), ATLETISMO (A) Y VOLEIBOL (V), SI 74 PRACTICAN
V, 92 PRACTICAN A, 117 PRACTICAN F, ADEMÁS 24
PRACTICAN V Y F, 22 PRACTICAN F Y A, 19 PRACTICAN V Y A Y
9 LOS TRES DEPORTES. REALIZAR UN DIAGRAMA DE VENN Y
RESPONDER:
a) ¿CUÁNTOS ALUMNOS NO PRACTICAN ALGUNO DE ESTOS
TRES DEPORTES?
b) ¿CUÁNTOS PRACTICAN SÓLO F Y V?
c) ¿CUÁNTOS ALUMNOS PRACTICAN SÓLO UN DEPORTE?

8. Conjunto Universo y Conjunto Unitario
• Universo: Esta formado
por todos los elementos
que intervienen en una
situación dada.
Ejemplo:
U = x x es un Estado de la
República Mexicana
• Unitario: Consta de un
solo elemento.
Ejemplo:
M = x x es maestra de
Álgebra de Prepa UPAEP
Santiago de 1º B
A = x x es alumno de
primer semestre de
Bachillerato de UPAEP de
nombre René Santos
Gómez

9. Representación de Subconjuntos
Los representaremos ahora con un diagrama
de Venn.
K
1 3
7
2 6
10
5 8 9
4
M L

10. PROPIEDADES DE LOS SUBCONJUNTOS
1) Cualquier conjunto esta incluido en si mismo, es
decir es subconjunto de sí mismo. A  A
2) El conjunto vacio es un subconjunto de cualquier
conjunto.   A. ¿Por qué? Como el conjunto
no tiene elementos, si no fuera así, significaría
que alguno de sus elementos no esta en otro.
3) Al conjunto que contiene todos los elementos se
le denomina Conjunto Universal.

11. EJEMPLO
Sea Z = l, m, n
Escribir todos los posibles subconjuntos de Z:
, l, m, n, l, m, m, n, l, n, l, m, n

12. COMPLEMENTO DE UN
SUBCONJUNTO
Si tenemos un conjunto U = 1, 2, 3, 4, 5, 6, 7 y
otro B = 3, 7, decimos que B es subconjunto
de U.
Los elementos 1, 2, 4, 5, 6 están en U pero no
están en B, este conjunto se representa como
Bc o B’ y se lee “complemento de B” o “B
prima”.
B’ = 1, 2, 4, 5, 6
Su notación sería B’ = x  U  x  B

13. Ejemplos de Complemento de un
Subconjunto
Si U = 1, 2, 3… 20 y A  U y sabemos que:
A = x  x es un número par menor o igual a 20,
encontrar A’
A = 2, 4, 6, 8, 10, 12, 14, 16, 18, 20
A’ = x  x es un número non menor a 20
A’ = 1, 3, 5, 7, 9, 11, 13, 15, 17, 19
A’ = x  U  x  A

14. Ejemplos de Complemento de un
Subconjunto
Si U = a, b, c, d, e, f, g, h, i, j y S  U y sabemos
que:
S = a, g, h, i, encontrar S’
S’ = b, c, d, e, f, j
S’ = x  U  x  S

15. EQUIVALENCIA ENTRE
PROBABILIDAD Y CONJUNTOS.
– Tirar una moneda tres veces
• Espacio muestral
– Ω = {CCC, CCX, CXC, CXX, XCC, XCX, XXC, XXX}.
– Sucesos simples: cada uno de los elementos de Ω
– Otros ejemplos de sucesos podrían ser,
• A = {dos caras como mínimo}
– A = {CCC, CCX,CXC, XCC}.
• B = {dos cruces}
– B = {CXX, XCX,XXC}