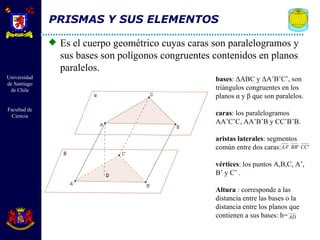
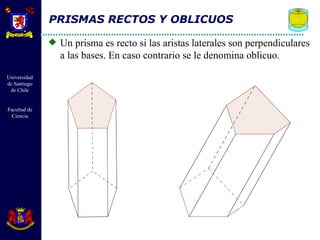
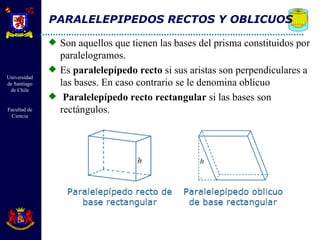
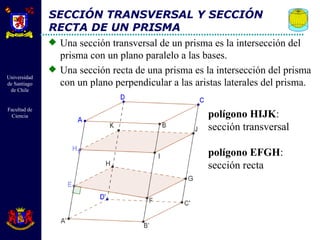
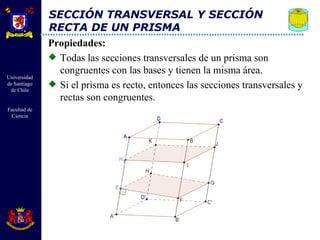
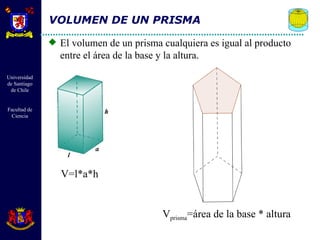
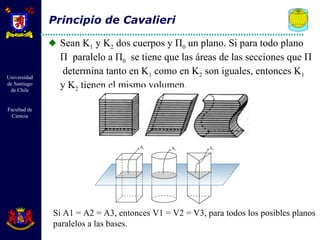
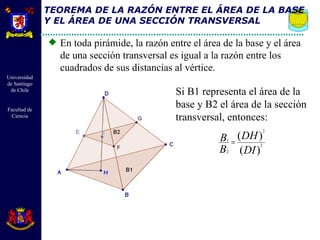
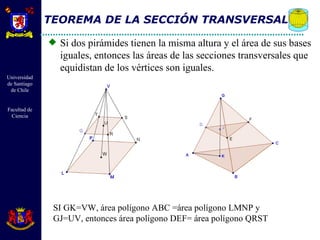
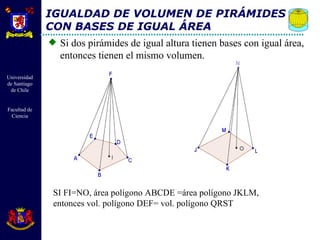
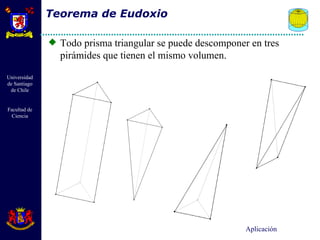
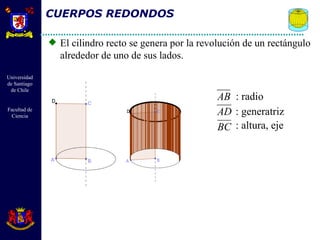
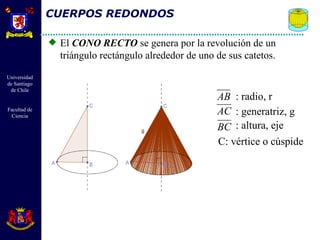
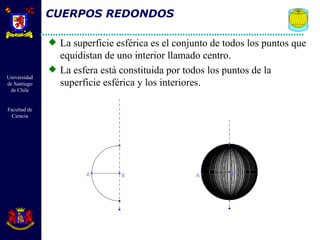
El documento describe diferentes cuerpos geométricos como prismas, paralelepípedos, pirámides y cuerpos redondos. Define sus elementos, propiedades y fórmulas para calcular su área, volumen y otras medidas. También explica conceptos como secciones transversales, teoremas sobre volúmenes e igualdades, y la generación de cuerpos por rotación.

1. Curso : “ Geometría ” Unidad: “ Cuerpo Geométricos ” Santiago, diciembre de 2009

2. PRISMAS Y SUS ELEMENTOS Es el cuerpo geométrico cuyas caras son paralelogramos y sus bases son polígonos congruentes contenidos en planos paralelos. bases : Δ ABC y Δ A’B’C’, son triángulos congruentes en los planos α y β que son paralelos. caras : los paralelogramos AA’C’C, AA’B’B y CC’B’B. aristas laterales : segmentos común entre dos caras: vértices : los puntos A,B,C, A’, B’ y C’ . Altura : corresponde a las distancia entre las bases o la distancia entre los planos que contienen a sus bases: h=

3. PRISMAS RECTOS Y OBLICUOS Un prisma es recto si las aristas laterales son perpendiculares a las bases. En caso contrario se le denomina oblicuo.

4. PARALELEPIPEDOS RECTOS Y OBLICUOS Son aquellos que tienen las bases del prisma constituidos por paralelogramos. Es paralelepípedo recto si sus aristas son perpendiculares a las bases. En caso contrario se le denomina oblicuo Paralelepípedo recto rectangular si las bases son rectángulos.

5. SECCIÓN TRANSVERSAL Y SECCIÓN RECTA DE UN PRISMA Una sección transversal de un prisma es la intersección del prisma con un plano paralelo a las bases. Una sección recta de una prisma es la intersección del prisma con un plano perpendicular a las aristas laterales del prisma. polígono HIJK : sección transversal polígono EFGH : sección recta

6. SECCIÓN TRANSVERSAL Y SECCIÓN RECTA DE UN PRISMA Propiedades: Todas las secciones transversales de un prisma son congruentes con las bases y tienen la misma área. Si el prisma es recto, entonces las secciones transversales y rectas son congruentes.

7. ÁREA LATERAL Y ÁREA TOTAL DE UN PRISMA El área lateral de un prisma se obtiene al sumar las áreas de las caras laterales. El área total de un prisma resulta al sumar las áreas de las caras laterales y las de las bases. á lat. prisma = l*p á total prisma = 2B +l*p l : longitud arista lateral p : perímetro de la sección recta. B : área de la base.

8. VOLUMEN DE UN PRISMA El volumen de un prisma cualquiera es igual al producto entre el área de la base y la altura. V=l*a*h V prisma =área de la base * altura

9. Principio de Cavalieri Sean K 1 y K 2 dos cuerpos y П 0 un plano. Si para todo plano П paralelo a П 0 se tiene que las áreas de las secciones que П determina tanto en K 1 como en K 2 son iguales, entonces K 1 y K 2 tienen el mismo volumen. Si A1 = A2 = A3, entonces V1 = V2 = V3, para todos los posibles planos paralelos a las bases.

10. Pirámide Es un poliedro que tiene como base un polígono cualquiera y sus caras laterales son triángulos que tienen un vértice común llamado cúspide o vértice de la pirámide. Dependiendo de la base: triangulares, cuadradas, pentagonales, hexagonales, etc. Pirámide Regular: L : vértice o cúspide Polígono ABCD : cuadrado. LK : altura. LE : apotema, ρ Δ ABL, Δ BCL, Δ CDL y Δ DAL : triángulos isósceles congruentes.

11. TEOREMA DE LA RAZÓN ENTRE EL ÁREA DE LA BASE Y EL ÁREA DE UNA SECCIÓN TRANSVERSAL En toda pirámide, la razón entre el área de la base y el área de una sección transversal es igual a la razón entre los cuadrados de sus distancias al vértice. Si B1 representa el área de la base y B2 el área de la sección transversal, entonces:

12. TEOREMA DE LA SECCIÓN TRANSVERSAL Si dos pirámides tienen la misma altura y el área de sus bases iguales, entonces las áreas de las secciones transversales que equidistan de los vértices son iguales. SI GK=VW, área polígono ABC =área polígono LMNP y GJ=UV, entonces área polígono DEF= área polígono QRST

13. IGUALDAD DE VOLUMEN DE PIRÁMIDES CON BASES DE IGUAL ÁREA Si dos pirámides de igual altura tienen bases con igual área, entonces tienen el mismo volumen. SI FI=NO, área polígono ABCDE =área polígono JKLM, entonces vol. polígono DEF= vol. polígono QRST

14. Teorema de Eudoxio Todo prisma triangular se puede descomponer en tres pirámides que tienen el mismo volumen. Aplicación

15. Volumen de una Pirámide El volumen de una pirámide cualquiera es igual al producto entre el área de la base y su altura. V pirámide =

16. CUERPOS REDONDOS Los cuerpos redondos están limitados solamente por superficies curvas o bien por superficies planas y curvas. Se pueden considerar como volúmenes o cuerpos de revolución producidos al girar en torno a un eje una determinada figura geométrica.

17. CUERPOS REDONDOS El cilindro recto se genera por la revolución de un rectángulo alrededor de uno de sus lados. : radio : generatriz : altura, eje

18. CUERPOS REDONDOS Área lateral, área total y volumen del cilindro recto . área lateral cilindro : área total cilindro : Volumen cilindro :

19. CUERPOS REDONDOS El CONO RECTO se genera por la revolución de un triángulo rectángulo alrededor de uno de sus catetos. : radio, r : generatriz, g : altura, eje C: vértice o cúspide

20. CUERPOS REDONDOS Área lateral, área total y volumen del cono recto . área lateral cono : área total cono : Volumen cilindro :

21. CUERPOS REDONDOS La superficie esférica es el conjunto de todos los puntos que equidistan de uno interior llamado centro. La esfera está constituida por todos los puntos de la superficie esférica y los interiores.

22. CUERPOS REDONDOS Área y volumen de la esfera. área esfera: Volumen esfera :

23. CUERPOS REDONDOS Generación de cuerpos por Traslación y/o Rotación.

24. Teorema de Pappus -Guldin La superficie de un cuerpo de rotación es igual al producto del perímetro de la figura que la engendra por el camino recorrido por su centro de gravedad. A(Cuerpo de Revolución)= 2π ⋅ d ⋅ P d : distancia del eje de rotación al centro de gravedad de la región generadora. P : perímetro de la región generadora.

25. Teorema de Pappus -Guldin El Volumen de un cuerpo de rotación es igual al producto de la superficie de la figura que la engendra por el camino recorrido por su centro de gravedad. A(Cuerpo de Revolución)= 2π ⋅ d ⋅ A d : distancia del eje de rotación al centro de gravedad de la región generadora. A : Área de la región generadora.