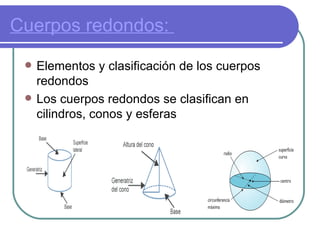
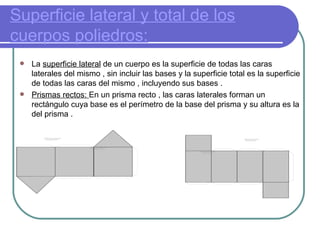
El documento presenta los conceptos básicos de los cuerpos geométricos incluyendo su clasificación, elementos, fórmulas para calcular su superficie y volumen. Explica que los poliedros se dividen en prismas y pirámides, y provee detalles sobre cada tipo de figura. También cubre cuerpos redondos como cilindros y conos, y cómo calcular su superficie total.

1. EVALUACION TRIMETRAL : Matemática Profesor : Jorge Moreira Alumnas : Alles Lourdes Araujo Carolina Ramírez marina Torres Noemí Curso : 3ro 3ra Colegio : Escuela normal José Manuel estrada “Regional”

2. Cuerpos geométricos : Elementos y clasificación de los cuerpos geométricos: Los poliedros se clasifican en prismas y pirámides. El prisma es un poliedro cuyas caras laterales son paralelogramos y las bases son polígonos paralelos e iguales . Clasificación de los prismas : _ Irregulares :sus bases son polígonos irregulares _ Regulares : sus bases son polígonos regulares . _ Rectos : sus caras laterales son rectángulos. La pirámides es un poliedro que tiene una sola base y un vértice o cúspide en el que concurren todas las caras menos una, que es la base. Clasificación de las pirámides : _ Irregular: su base es un polígono irregular. _ Regulares: su base es un polígono regular. _ Rectas: sus caras son triángulos isósceles iguales.

3. Cuerpos redondos: Elementos y clasificación de los cuerpos redondos Los cuerpos redondos se clasifican en cilindros, conos y esferas

4. Superficie lateral y total de los cuerpos poliedros: La superficie lateral de un cuerpo es la superficie de todas las caras laterales del mismo , sin incluir las bases y la superficie total es la superficie de todas las caras del mismo , incluyendo sus bases . Prismas rectos: En un prisma recto , las caras laterales forman un rectángulo cuya base es el perímetro de la base del prisma y su altura es la del prisma . Perímetro de la base Perímetro de la base

5. Poliedros regulares : Tetraedro regular: sus caras son cuatro triángulos equiláteros iguales . Hexaedro regular: sus caras son 6 caras iguales. Octaedro regular: sus caras son ocho triángulos equiláteros iguales . Dodecaedro regular: sus caras son 12 pentágonos regulares iguales Icosaedro regular: sus caras son 20 triángulos equiláteros iguales

6. Superficies laterales: Superficie lateral del prisma recto = perímetro de la base por la altura . La base de un prisma es un polígono , y para calcular la superficie de los mismos , se debe recurrir a las siguientes formulas: Triangulo : S= b . h 2 Cuadrado: S = Rectángulo : S = b . h Polígono regular : S = l . n . ap. n = a la cantidad de lados del polígono 2

7. Superficie total del prisma recto = superficie lateral + 2 . Superficie de la base . _ Sup. Lateral de la pirámide regular es = perímetro de la base . Altura de la cara lateral . 2 Sup. Total de la pirámide regular = superficie lateral + superficie de la base

8. Cuerpos redondos: Cilindro : la superficie total de un cilindro es la suma de la superficie de la cara lateral y la superficie d las bases En un cilindro , la cara lateral es un rectángulo cuya base es la longitud de la circunferencia de la base del cilindro y cuya altura es la altura del cilindro Superficie lateral del cilindro = 2. TT. r . H La base de un cilindro es un circulo cuya superficie es : TT . Superficie total del cilindro es = 2 . TT . h + 2 . TT . La longitud del arco del sector circular correspondiente a la cara lateral es la misma que la longitud de la circunferencia de la base del cono . La cara lateral de un cono es un sector circular cuya superficie es : Longitud del arco . Generatriz 2 La generatriz se calcula mediante la propiedad pitagórica . Cono: la superficie total de un cono es la suma de la de la base . superficie de la cara lateral y la superficie

9. Volumen del prisma y del cilindro Volumen del prisma: Volumen del prisma rectangular =largo . ancho . altura Para calcular el volumen de un prisma , cualquiera sea su base , se puede utilizar la siguiente formula : Volumen del prisma es = superficie de la base . Altura . En el caso del que el prisma sea un cubo , es decir que tiene todas las aristas iguales , se utiliza la siguiente forma . Volumen del cubo = arista . Arista . arista =

10. Volumen del cilindro Para explicar la formula se puede recurrir al siguiente razonamiento . Si en un prisma regular se aumenta cada ves mas la cantidad de lados de la base , se obtiene una figura geométrica plana que se aproxima cada ves mas a un circulo . Volumen del prisma es = superficie de la base . Altura de la cara lateral Volumen del cilindro es = superficie del cilindro . Altura Volumen del cilindro es = TT . . h

11. Volumen del la pirámide y del cono Volumen de la pirámide : Si se construye un prisma y una pirámide de igual base y altura , se observa a simple vista que el volumen de la pirámide es menor al realizar la experiencia de comparar el volumen de un prisma con una pirámide de igual base y altura usando arena o aserrín, se verifica que el volumen del prisma es 3 veces mayor que el de la pirámide. Volumen de la pirámide es = 1/3. superficie de la base. Altura

12. Volumen del cono Si se construye un cilindro y un cono de igual base y altura , la experiencia de comparar los volúmenes de ambos es similar a la del prisma y la pirámide . Volumen del cono = 1. superficie de la base. Altura 3

13. Volumen de la esfera se construye una semiesfera y un cono de igual altura radio que la semiesfera . Si se llena de agua el cono y se vierte su contenido el la semiesfera, se verifica que para llenar la semiesfera son necesarios exactamente 2conos La relación entre el volumen de un esfera y de un cono de igual altura y radio que el radio de la esfera es:

14. Volumen de la esfera : La relación entre el volumen de una esfera y de un cono de igual altura y radio que el radio de la esfera es : Volumen de media esfera=2.volumen del cono . Volumen de dos medias esferas=2.2.volumen del cono Volumen de una esfera es=4.volumen del cono Volumen de una esfera es =4. . TT. .r Volumen de esfera = .TT.

15. Unidades del volumen Los cuerpos ocupan un lugar en el espacio . Si se desea saber cuanto lugar ocupa , se debe medir su volumen . Medir es compara lo que se quiere con una unidad del mismo tipo que se utiliza como patrón . Para medir el volumen , la unidad que se utiliza es el metro cúbico ( ). Un metro cúbico es el volumen que se ocupa un cubo de un metro de arista. Para pasar de una unidad de volumen a una inmediata inferior , hay que multiplicar por 1000 y para pasar a una inmediata superior , hay que dividir por 1000 .

16. Unidades de volumen se lee se simboliza equivale a kilómetros cúbicos 1.000.000.000 Múltiplos hectómetro cúbico 1.000.000 decámetro cúbico 1.000 Unidad metros cúbico 1 decímetros cúbico 0.001 Submúltiplo centímetro cúbico 0,000001 milímetro cúbico 0,000000001