Descargado 29 veces
Subido porFernanda Meza Delgado
Circulo y cono
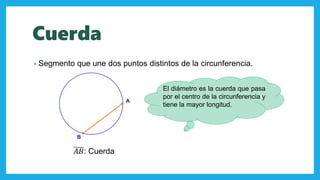
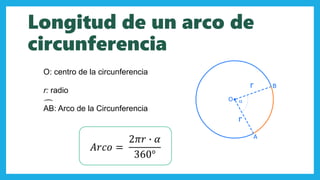
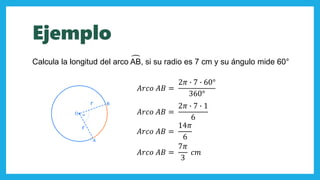
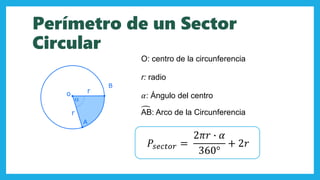
El documento abarca conceptos fundamentales de geometría, centrándose en la circunferencia, el círculo, y el cono. Se describen elementos como el radio, diámetro, cuerdas, secantes, y tangentes, así como fórmulas para calcular área y perímetro. Además, se explica el volumen y área total del cono, incluyendo ejemplos prácticos de cálculo.
Más contenido relacionado
Circulo y cono
- 1. UNIDAD: GEOMETRÍA Círculo yCircunferencia Área y Volumen del Cono
- 2. ELEMENTOS DE LA CIRCUNFERENCIAY CÍRCULO
- 3. Definición • Circunferencia: Líneacurva, cerrada y plana, cuyos puntos equidistan (igual distancia) de un punto fijo llamada centro. • Círculo: Región del plano limitado por una circunferencia.
- 4. Radio (r) • Segmentoque une el centro de la circunferencia con cualquier punto de la circunferencia. o r A O: Centro de la Circunferencia 𝑂𝐴: Radio = r
- 5. Diámetro (d) • Esla línea recta que pasa por el centro y une dos puntos de la circunferencia. • El diámetro divide a la circunferencia en 2 semicircunferencias iguales, es decir: 00 AB 00 BA A B rr d O •O: Centro de la Circunferencia 𝐴𝐵: Diámetro = d = 2r =
- 6. Cuerda • Segmento queune dos puntos distintos de la circunferencia. El diámetro es la cuerda que pasa por el centro de la circunferencia y tiene la mayor longitud. A B 𝐴𝐵: Cuerda
- 7. Secante • Recta queintersecta a la circunferencia en 2 puntos, formando una cuerda. A B • • 𝐴𝐵: Cuerda 𝐴𝐵: Secante
- 8. Tangente • Recta queintersecta en un solo punto a la circunferencia. Este punto es llamado “punto de tangencia” o “punto tangencial”. O: Centro de la circunferencia 𝑂𝐴: Radio L: Recta Tangente A: Punto de tangencia 𝑂𝐴 ⊥ 𝐿 L A r O
- 9. Arco de Circunferencia •Corresponde a una parte de la circunferencia. Su lectura es en sentido anti – horario. A B • • Los puntos A y B de la circunferencia, determinan el arco AB. 00 AB: Arco de la Circunferencia
- 10. Actividades 1. Identifica loselementos de la circunferencia 𝐴𝐵:______________ 𝑅𝑆:______________ 𝐸𝐹:______________ 𝐺𝐻: _____________ 𝑂𝐶:______________ 𝑂:_______________ 𝐾:_______________
- 11. Corona Circular • Esla superficie plana que se encuentra entre dos círculos concéntricos (de mismo centro). • El círculo mayor de radio es R • El círculo menor de radio es r r R
- 12. Sector Circular • Esuna fracción del área del círculo determinada por dos radios y un arco. Sector circular A B 00 AB: Arco de la Circunferencia O: centro de la circunferencia r: radio
- 13. Segmento Circular • Esuna parte del área del círculo, determinada por una cuerda y un arco de la circunferencia. 00 AB: Arco de la Circunferencia O: centro de la circunferencia 𝐴𝐵: Cuerda B A Segmento circular
- 14.
- 15. Área del Círculo •Si r es el radio, entonces: Á𝑟𝑒𝑎 𝑐𝑖𝑟𝑐𝑢𝑙𝑜 = 𝜋 ∙ 𝑟2 o r A
- 16. Área del Círculo •Ejemplo: Determinar el área del círculo cuyo diámetro mide 20 cm. • Respuesta: Si el diámetro mide 20 cm, entonces el radio es 10 cm. Luego, el área del círculo es: 𝐴 = 𝜋 ∙ 102 ⇒ 𝐴 = 100𝜋𝑐𝑚2
- 17. Perímetro de la Circunferencia •Si r es el radio y d el diámetro, entonces: 𝑃𝑒𝑟í𝑚𝑒𝑡𝑟𝑜 = 2𝜋𝑟o r A
- 18. Perímetro de la Circunferencia •Ejemplo: Determinar el perímetro de una circunferencia cuyo radio mide 15 cm. • Respuesta: 𝑃 = 2𝜋 ∙ 15 ⇒ 𝑃 = 30𝜋 𝑐𝑚
- 19. Ejercicio • Calcula elárea y perímetro de la zona achurada
- 20. Ejercicio • Calcula elárea y perímetro de la figura
- 21. 00 Longitud de unarco de circunferencia 𝐴𝑟𝑐𝑜 = 2𝜋𝑟 ∙ 𝛼 360° O: centro de la circunferencia r: radio AB: Arco de la Circunferencia
- 22. 𝐴𝑟𝑐𝑜 𝐴𝐵 = 2𝜋∙ 7 ∙ 60° 360° Calcula la longitud del arco AB, si su radio es 7 cm y su ángulo mide 60° 00 𝐴𝑟𝑐𝑜 𝐴𝐵 = 2𝜋 ∙ 7 ∙ 1 6 𝐴𝑟𝑐𝑜 𝐴𝐵 = 14𝜋 6 𝐴𝑟𝑐𝑜 𝐴𝐵 = 7𝜋 3 𝑐𝑚 Ejemplo
- 23. • Calcula lalongitud de cada arco de circunferencia O. Ejercicios 𝐿 𝐴𝐵 = 2𝜋 𝑐𝑚 00 𝐿 𝐸𝐹 = 7 9 𝜋 𝑐𝑚 00 𝐿 𝐻𝐺 = 00 50 9 𝜋 𝑐𝑚
- 24. • Calcula lalongitud de cada arco de circunferencia O. Ejercicios 𝐿 𝐴𝐵 = 5 3 𝜋 𝑐𝑚 00 𝐿 𝐶𝐷 = 𝜋 𝑐𝑚 00 𝐿 𝐸𝐹 = 2𝜋 𝑐𝑚 00
- 25. Área de unSector Circular Á𝑟𝑒𝑎 𝑠𝑒𝑐𝑡𝑜𝑟 = 𝛼 ∙ 𝜋𝑟2 360° A B 00 O: centro de la circunferencia r: radio 𝛼: Ángulo del centro AB: Arco de la Circunferencia Área de un Sector Circular
- 26. 𝑃𝑠𝑒𝑐𝑡𝑜𝑟 = 2𝜋𝑟 ∙𝛼 360° + 2𝑟 A B 00 O: centro de la circunferencia r: radio 𝛼: Ángulo del centro AB: Arco de la Circunferencia Perímetro de un Sector Circular
- 27. Ejemplo 1 Determinar elárea y perímetro de la zona achurada de la figura. O: centro de la circunferencia. A B • O 3 60º 𝐴 𝑠𝑒𝑐𝑡𝑜𝑟 = 60 ∙ 𝜋 ∙ 32 360° 𝐴 𝑠𝑒𝑐𝑡𝑜𝑟 = 1 ∙ 𝜋 ∙ 9 6 𝐴 𝑠𝑒𝑐𝑡𝑜𝑟 = 3𝜋 2 𝑃𝑠𝑒𝑐𝑡𝑜𝑟 = 2 ∙ 𝜋 ∙ 3 ∙ 60° 360° + 2 ∙ 3 𝑃𝑠𝑒𝑐𝑡𝑜𝑟 = 𝜋 + 6
- 28. Área de unSegmento Circular B A a 𝐴 𝑠𝑒𝑔𝑚𝑒𝑛𝑡𝑜 = 𝐴 𝑠𝑒𝑐𝑡𝑜𝑟 − 𝐴 𝑡𝑟𝑖á𝑛𝑔𝑢𝑙𝑜 𝑂𝐴𝐵 00 O: centro de la circunferencia r: radio 𝛼: Ángulo del centro AB: Arco de la Circunferencia
- 29. Perímetro de unSegmento Circular B A a 𝑃𝑠𝑒𝑔𝑚𝑒𝑛𝑡𝑜 = 2𝜋𝑟 ∙ 𝛼 360° + 𝐴𝐵 00 O: centro de la circunferencia r: radio 𝛼: Ángulo del centro AB: Arco de la Circunferencia
- 30. Ejemplo 2 Determinar elárea y perímetro de la zona achurada de la figura. O: centro de la circunferencia. O A B5 • • • 𝑃𝑠𝑒𝑔𝑚𝑒𝑛𝑡𝑜 = 2𝜋 ∙ 8 ∙ 90 360° + 4 8 𝑃𝑠𝑒𝑔𝑚𝑒𝑛𝑡𝑜 = 2𝜋 ∙ 8 ∙ 1 4 + 4 8 𝑃𝑠𝑒𝑔𝑚𝑒𝑛𝑡𝑜 = 4𝜋 + 4 8 𝑐𝑚 𝑃𝑠𝑒𝑔𝑚𝑒𝑛𝑡𝑜 = 4 𝜋 + 2 8 𝑐𝑚
- 31. Continuación 𝐴 𝑠𝑒𝑔𝑚𝑒𝑛𝑡𝑜 =16𝜋 𝑐𝑚2 − 32𝑐𝑚2 𝐴 𝑠𝑒𝑔𝑚𝑒𝑛𝑡𝑜 = 16 𝜋 − 2 𝑐𝑚2 𝐴 𝑡𝑟𝑖á𝑛𝑔𝑢𝑙𝑜 𝑂𝐴𝐵 = 8 ∙ 8 2 𝐴 𝑡𝑟𝑖á𝑛𝑔𝑢𝑙𝑜 𝑂𝐴𝐵 = 32 𝑐𝑚2 𝐴 𝑠𝑒𝑔𝑚𝑒𝑛𝑡𝑜 = 𝐴 𝑠𝑒𝑐𝑡𝑜𝑟 − 𝐴 𝑡𝑟𝑖á𝑛𝑔𝑢𝑙𝑜 𝑂𝐴𝐵 𝐴 𝑠𝑒𝑐𝑡𝑜𝑟 = 90 ∙ 𝜋 ∙ 82 360° 𝐴 𝑠𝑒𝑐𝑡𝑜𝑟 = 1 ∙ 𝜋 ∙ 64 4 𝐴 𝑠𝑒𝑐𝑡𝑜𝑟 = 16𝜋 𝑐𝑚2
- 32. • Calcula elperímetro de cada sector o segmento circular Ejercicios a) b) c)
- 33. • Calcula elperímetro de cada sector o segmento circular Ejercicios d) e) f)
- 34. • Calcula elárea de cada sector circular Ejercicios
- 35. • Calcula elárea de cada segmento circular Ejercicios
- 37. Definición • Un cuerpogeométrico o sólido es todo lo que ocupa en el espacio. • Los cuerpos geométricos pueden ser de dos clases: — Formados por caras planas (POLIEDROS) — Formados por caras curvas (CUERPOS REDONDOS)
- 38. Cuerpo Geométrico Poliedro Cuerpo Redondo RegularesIrregulares Dodecaedro Icosaedro Tetraedro Octaedro Prisma Recto Prisma Inclinado Pirámide Cilindro Cono Tronco Esfera
- 39. Poliedros Regulares 4 caras6 caras 8 caras 12 caras 20 caras
- 40.
- 41.
- 42. OBS: Cada cuerpogeométrico o sólido tiene volumen y área. Volumen: Lugar que ocupa en el espacio (Capacidad) Área Total: Superficie de cada figura que forma el cuerpo geométrico.
- 44. Definición • Son aquelloscuerpos o sólidos geométricos formados por regiones curvas, o regiones planas y curvas. • Se generan por la rotación de 360° indefinida de una figura plana alrededor de su eje. • El cuerpo redondo que estudiaremos, será el CONO.
- 45. Cono • Corresponde alcuerpo generado por la rotación indefinida de un triangulo rectángulo alrededor de uno de sus catetos.
- 46. Cono • La basedel cono es una circunferencia; el vértice superior del triangulo es el vértice del cono; la distancia entre la base y el vértice es la altura; y la hipotenusa del triangulo es la generatriz. Vértice del cono Generatriz (g) h Altura (h)
- 47.
- 48. h r Á𝑟𝑒𝑎 𝑡𝑜𝑡𝑎𝑙 =𝜋 ∙ 𝑟 ∙ 𝑔 + 𝜋𝑟2 𝑉𝑜𝑙𝑢𝑚𝑒𝑛 = 𝜋𝑟2 ∙ ℎ 3 Á𝑟𝑒𝑎 𝑡𝑜𝑡𝑎𝑙 = 𝐴𝑙𝑎𝑡𝑒𝑟𝑎𝑙 + 𝐴 𝑏𝑎𝑠𝑎𝑙 g
- 49. Ejemplo • Hallar elárea total de un cono si la generatriz vale 9 cm y el radio de la base 5 cm h 5 9 Á𝑟𝑒𝑎 𝑡𝑜𝑡𝑎𝑙 = 𝜋 ∙ 𝑟 ∙ 𝑔 + 𝜋𝑟2 Á𝑟𝑒𝑎 𝑡𝑜𝑡𝑎𝑙 = 𝜋 ∙ 5 ∙ 9 + 𝜋 ∙ 52 Á𝑟𝑒𝑎 𝑡𝑜𝑡𝑎𝑙 = 45𝜋 + 25𝜋 Á𝑟𝑒𝑎 𝑡𝑜𝑡𝑎𝑙 = 70𝜋 𝑐𝑚2
- 50. Ejemplo • Calcula elvolumen del cono, si su generatriz es 5 cm y su radio 3 cm h 3 5 𝑉𝑜𝑙𝑢𝑚𝑒𝑛 = 𝜋𝑟2 ∙ ℎ 3ℎ2 = 52 − 32 ℎ2 = 25 − 9 ℎ2 = 16 ℎ = 16 ℎ = 4 𝑉𝑜𝑙𝑢𝑚𝑒𝑛 = 𝜋 ∙ 32 ∙ 4 3 𝑉𝑜𝑙𝑢𝑚𝑒𝑛 = 36𝜋 3 𝑉𝑜𝑙𝑢𝑚𝑒𝑛 = 12𝜋 𝑐𝑚3