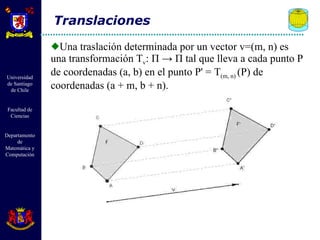
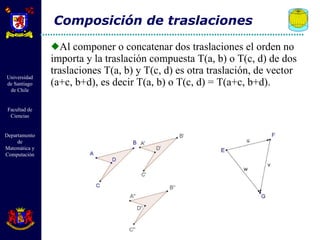
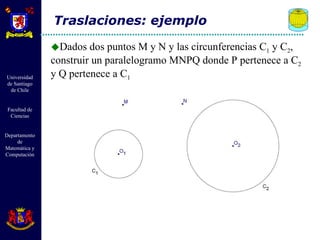
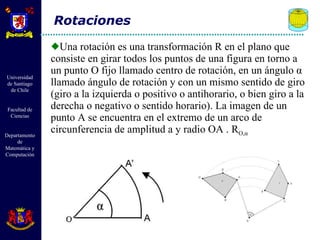
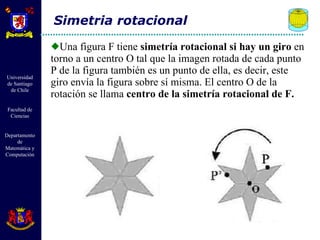
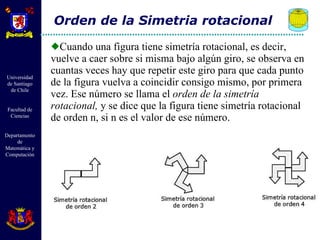
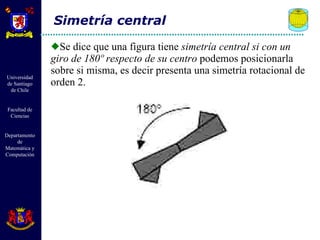
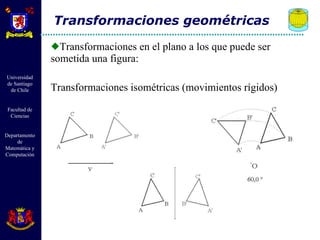
El documento describe diferentes tipos de transformaciones isométricas en geometría euclidiana, incluyendo traslaciones, rotaciones y reflexiones. Las traslaciones mueven cada punto de una figura por un mismo vector. Las rotaciones giran todos los puntos de una figura alrededor de un punto fijo. Las reflexiones crean puntos simétricos de cada punto a través de un eje. Estas transformaciones preservan distancias y ángulos.

1. Curso : “ Geometría Euclidiana ” Unidad: “ Transformaciones Isométricas ” Santiago, 09 de diciembre de 2008

2. Motivación Isometrías Simetrías Congruencias

3. la simetría resulta de la proporción de cada parte y de su proporción respecto del todo. Desde la intuición

4. Se llamará isometría del plano a cualquier función o transformación del plano en si mismo que no cambie la distancia entre los puntos originales y sus imágenes. Dos objetos del plano se llaman “ congruentes ” si hay una isometría que lleve a uno en el otro; es decir, si podemos transformar (sobreponer) uno en el otro través de un movimiento. Desde la intuición

5. Una transformación consiste en asociar a cada punto P del plano Π otro punto P’ de acuerdo a una regla preestablecida. Una transformación geométrica es la correspondencia entre puntos “origen” y puntos “imagen”, el transformado de llama homólogo del original y estará relacionado de alguna forma con la figura original. Se debe tener presente: La figura original. Una regla u operación que describa el cambio, y La figura que resulta después del cambio. Transformaciones geométricas

6. Transformaciones en el plano a los que puede ser sometida una figura: Transformaciones isométricas (movimientos rígidos) Transformaciones geométricas

7. Transformaciones en el plano a los que puede ser sometida una figura: Transformaciones homotéticas (figuras a escala) Transformaciones afines Transformaciones geométricas

8. Transformaciones en el plano a los que puede ser sometida una figura: Transformaciones proyectivas (geometría de las sombras) Transformaciones topológicas Transformaciones geométricas

9. Dada una transformación T, que a cada punto P de un plano Π le hace corresponder un punto P’=T(P) de Π . Se dice que T es una Isometría , si y sólo si, cuando: d[A,B]=d[T(A),T(B)] para cualquier par de puntos A y B del plano Π . Toda Isometría posee las siguientes propiedades: a.- La imagen de una recta por una isometría es una recta. b.- una Isometría preserva el paralelismo. c.- preserva ángulos. Como consecuencia de la definición, la imagen de una figura F por una Isometría, es una figura F’ congruente a F. Transformaciones isométricas

10. Una traslación determinada por un vector v=(m, n) es una transformación T v : Π -> Π tal que lleva a cada punto P de coordenadas (a, b) en el punto P' = T (m, n) (P) de coordenadas (a + m, b + n). Translaciones

11. La traslación de un punto P en un vector V, envía a P en otro punto P', donde el vector PP' tiene la misma dirección, sentido y magnitud que el vector V. Es decir el vector V es equipolente al vector PP'. Al punto P' se le llama homólogo de P. La traslación de una figura F, según un vector V, es otra figura F' que resulta de trasladar cada uno de los puntos de F según el vector V. Translaciones

12. Una traslación es una transformación que mantiene invariantes objetos y relaciones. Región interior y exterior de una figura. Distancias entre dos puntos de una figura (por ende, el perímetro). Orden de los puntos en una recta. Líneas rectas. Convexidad. Paralelismo. Medidas de ángulos. Área. Invariantes bajo una Translación

13. Al componer o concatenar dos traslaciones el orden no importa y la traslación compuesta T(a, b) o T(c, d) de dos traslaciones T(a, b) y T(c, d) es otra traslación, de vector (a+c, b+d), es decir T(a, b) o T(c, d) = T(a+c, b+d). Composición de traslaciones

14. Dados dos puntos M y N y las circunferencias C 1 y C 2 , construir un paralelogramo MNPQ donde P pertenece a C 2 y Q pertenece a C 1 Traslaciones: ejemplo

15. Una rotación es una transformación R en el plano que consiste en girar todos los puntos de una figura en torno a un punto O fijo llamado centro de rotación, en un ángulo α llamado ángulo de rotación y con un mismo sentido de giro (giro a la izquierda o positivo o antihorario, o bien giro a la derecha o negativo o sentido horario). La imagen de un punto A se encuentra en el extremo de un arco de circunferencia de amplitud a y radio OA . R O, α Rotaciones

16. Rotaciones en el plano cartesiano

17. Una rotación es una transformación que mantiene invariantes objetos y relaciones. Región interior y exterior de una figura. Distancias entre dos puntos de una figura (por ende, el perímetro). Orden de los puntos en una recta. Líneas rectas. Convexidad. Medidas de ángulos. Área. Centros de rotación. Invariantes bajo una Rotación

18. El resultado de componer dos rotaciones del mismo centro no depende del orden y es una nueva rotación, con el mismo centro, en un ángulo igual a la suma de los ángulos de las dos rotaciones. La notación es : R P, α o R P, β = R P, α + β , cualesquiera que sea el punto P y los ángulos α y β . Composición de rotaciones

19. Una figura F tiene simetría rotacional si hay un giro en torno a un centro O tal que la imagen rotada de cada punto P de la figura también es un punto de ella, es decir, este giro envía la figura sobre sí misma. El centro O de la rotación se llama centro de la simetría rotacional de F. Simetria rotacional

20. Cuando una figura tiene simetría rotacional, es decir, vuelve a caer sobre si misma bajo algún giro, se observa en cuantas veces hay que repetir este giro para que cada punto de la figura vuelva a coincidir consigo mismo, por primera vez. Ese número se llama el orden de la simetría rotacional, y se dice que la figura tiene simetría rotacional de orden n, si n es el valor de ese número. Orden de la Simetria rotacional

21. Se dice que una figura tiene simetría central si con un giro de 180º respecto de su centro podemos posicionarla sobre si misma, es decir presenta una simetría rotacional de orden 2. Simetría central

22. Dada una recta L, se dice que un punto P’ es simétrico de un punto P en relación de L, cuando L es simetral de PP’. Una reflexión en torno de una recta L es una transformación R L que hace corresponder a cada punto P del plano a un punto P’= R L (P), simétrico de P en relación de L. a. El segmento PP' es perpendicular a L. b. Los puntos P y P' equidistan del eje L (longitud de es igual a la longitud de ). Reflexiones

23. Dados dos puntos A y B de un mismo lado de una recta r. Determinar un punto P sobre r de forma que PA + PB sea mínimo. Reflexiones: ejemplo

24. Si una figura o un conglomerado de figuras queda invariante (es enviada en sí misma) por alguna reflexión, decimos que esta figura goza de la propiedad de simetría axial, o más brevemente, que tiene simetría axial. El eje de esta reflexión se llama eje de simetría de la figura. Simetría Axial

25. Una reflexión es una transformación que mantiene invariantes objetos y relaciones. Región interior y exterior de una figura. Distancias entre dos puntos de una figura (por ende, el perímetro). Orden de los puntos en una recta. Líneas rectas. Convexidad. Medidas de ángulos. Área. El eje de reflexión Invariantes bajo una Reflexión

26. El resultado de componer dos reflexiones, con ejes paralelos denotados r y s, es una traslación perpendicular a los ejes y de una magnitud igual al doble de la distancia que los separa. Composición de Reflexiones

27. Si los ejes de reflexión se cortan, se una rotación, cuyo centro es justamente el punto de intersección de los dos ejes de reflexión, y cuyo ángulo es ... El doble del ángulo que forman los dos ejes de reflexión. Composición de Reflexiones