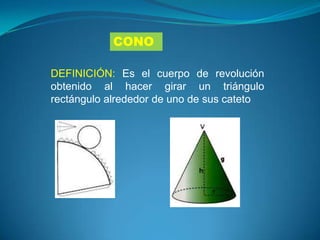
Este documento proporciona definiciones, elementos y fórmulas para calcular el área y volumen de varias figuras geométricas tridimensionales como prismas, pirámides, cilindros, conos y esferas. Explica que los prismas tienen dos bases paralelas y caras laterales en forma de paralelogramos, mientras que las pirámides tienen una base poligonal y caras triangulares. También describe que los cilindros y conos se forman por la rotación de un rectángulo y triángulo rect

1. PROFESOR: Rubén Wilfredo DIAZ A.

2. TEMA: FIGURAS SOLIDAS
PRISMAS
PIRÁMIDES
CILINDRO
CONO
ESFERA

3. DEFINICIÓN: ES UN POLIEDRO, QUE TIENE DOS CARAS
PARALELAS E IGUALES LLAMADAS BASES Y SUS CARAS
LATERALES SON PARALELOGRAMOS.
Base
Caras laterales

4. ELEMEN TOS:
Bases o caras básicas: dos
polígonos iguales situados en
planos paralelos.
Caras laterales, que son
paralelogramos.
Aristas básicas: los lados de
los polígonos de las bases.
Aristas laterales: los lados de
las caras laterales.
Vértices: los puntos donde se
cortan las aristas.
Altura de un prisma: la
distancia entre las bases
http://pe.kalipedia.com/matematicas-geometria/tema/poliedros/elementos-prisma.html?x=20070926klpmatgeo_297.Kes&ap=0

5. CLASIFICACION:
Prismas oblicuos: Cuando las
aristas laterales son oblicuos a
las bases.
Prisma rectos: Las aristas
laterales son perpendiculares a
las bases.
Prisma Regular: Es un
prisma recto con polígonos
regulares como bases.

6. TIPOS DE PRISMA SEGÚN SU BASE
Prisma triangular Prisma cuadrangular
Prisma pentagonal
Prisma Hexagonal

7. Paralelepípedos Los paralelepípedos son los prismas cuyas bases son
paralelogramos.
Los ortoedros son paralelepípedos que tienen todas
Ortoedros
sus caras rectangulares.

8. ÁREA Y VOLUMEN DEL PRISMA
AREA LATERAL (AL) : Perímetro de la bases x altura
AREA TOTAL (AT): Área Lateral + 2 (Área de la bases)
VOLUMEN DEL PRISMA (V): Área de la base x altura
EVALUACIÓN
En esta pagina web el alumno se autoevaluara su aprendizaje
http://www.quia.com/hm/238578.html?AP_rand=1472275111

9. PIRÁMIDE
DEFINICIÓN: Poliedros cuya base es un polígono
cualquiera y cuyas caras laterales son triángulos con un
vértice común, que es el vértice de la pirámide.

10. ELEMEN TOS DE UNA PIRÁMIDE:
1. La altura de la pirámide es
el segmento perpendicular a la
base, que une la base con el
vértice.
2. La apotema de la Pirámide es la
altura de cualquiera de sus caras
laterales.
3. Las aristas de la base se llaman
aristas básicas y las aristas que
concurren en el vértice, aristas
laterales.

11. Clasificación de las
pirámides
Por su forma
Pirámide regular: La
base es un polígono
regular y la altura cae
en el centro
Pirámide irregular:
La base no es
polígono regular.

12. Por el número de lados de la base:
Pirámide triangular Pirámide cuadrangular
Pirámide pentagonal Pirámide hexagonal

13. ÁREA Y VOLUMEN DE LA PIRAMIDE:
Área lateral (AL): suma de áreas de caras laterales
Área total (AT): área lateral + área de la base
Volumen: área de la base x altura/3
Pirámide regular
AL = p x Ap AT= p(Ab - Ap)
P = Semiperimetro
Ab = Apotemas de la base
Ap = Apotema de la Piramide

14. CILINDRO
DEFINICION: Es el cuerpo engendrado por un rectángulo
que gira alrededor de uno de sus lados.

15. ELEMEN TOS DE UN CILINDRO
EJE: Es El lado fijo alrededor del cual gira el rectángulo
GENERATRIZ: Es el lado opuesto al eje, y es el lado
que engendra el cilindro.
BASES: Son los círculos que engendran
los lados perpendiculares al eje
ALTURA: Es la distancia entre las dos bases,
esta distancia es igual a la generatriz.

16. ÁREA Y VOLUMEN DEL CILINDRO
ÁREA LATERAL (AL )= 2πRg
ÁREA DE BASE(Ab) = π R²
ÁREA TOTAL ( AT) = área lateral + 2área de la base
(AT) = 2πRg + 2πR²
(AT) = 2πR(g + R)
VOLUMEN (V) = π R ² H

17. CONO
DEFINICIÓN: Es el cuerpo de revolución
obtenido al hacer girar un triángulo
rectángulo alrededor de uno de sus cateto

18. ELEMENTOS DEL CONO
EJE: Es el cateto fijo alrededor del cual gira el triángulo
GENERATRIZ: Es la hipotenusa del triángulo rectángulo.
ALTURA: Es la distancia del vértice a la base.
BASE: Es el círculo que forma el otro cateto

19. ÁREAS Y VOLUMEN
DEL CONO
ÁREA LATERAL (AL) = πRg
ÁREA DE LA BASE (Ab) = πR²
ÁREA TOTAL (AT ) = área lateral + área de la base
= πRg + πR²
= πR(g + R)
VOLUMEN = (Área de la base x altura)/3
= πR²h/3

20. ESFERA
Superficie esférica
Es la superficie engendrada por una circunferencia
que gira sobre su diámetro.
Esfera
Es la región del espacio que se encuentra en el interior
de una superficie esférica

21. ELEMENTOS DE LA ESFERA
Centro
Punto interior que equidista de cualquier punto de la esfera.
Radio
Distancia del centro a un punto de la esfera.
Cuerda
Segmento que une dos puntos de la superficie.
Diámetro
Cuerda que pasa por el centro.
Polos
Son los puntos del eje de giro que quedan sobre la superficie
esférica.

22. Circunferencias en una esfera
Paralelos
Circunferencias obtenidas al cortar la superficie esférica con
planos perpendiculares al eje de revolución.
Ecuador
Circunferencia obtenida al cortar la superficie esférica con el
plano perpendicular al eje de revolución que contiene al centro
de la esfera.s
meridiano
Circunferencias obtenidas al cortar la superficie esférica con
planos que contienen el eje de revolución.

23. Figuras geométricas en la esfera
HEMISFERIO
Es cada una de las partes
en que queda dividida la
superficie esférica por un
plano que pasa por el
centro de la esfera,
llamado plano diametral.
SEMIESFERA
Parte de una esfera
comprendida entre dos
planos que se cortan en
el diámetro de aquella.

24. HUSO ESFERICO
Parte de la superficie de
una esfera comprendida
entre dos planos que se
cortan en el diámetro de
aquella.
CUÑA ESFERICA
Parte de una esfera
comprendida entre dos
planos que se cortan en el
diámetro de aquella.

25. CASQUETE ESFÉRICO
Es cada una de las partes de la
esfera determinada por un plano
secante.
ZONA ESFÉRICA
Es la parte de la esfera
comprendida entre dos planos
secantes paralelos.

26. ÁREA Y VOLUMEN DE LA ESFERA