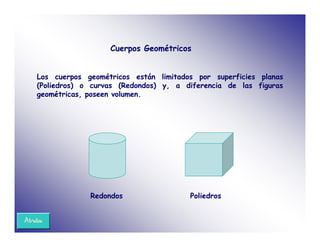
El documento proporciona información sobre diferentes tipos de cuerpos geométricos, incluyendo poliedros, pirámides, prismas, cilindros, conos y esferas. Describe sus características y cómo calcular su área y volumen. Explica que los poliedros pueden ser regulares u irregulares, y que los regulares son los sólidos platónicos.

1. Teresa Pérez Díaz
Pé Dí
Profesora de matemática
matemá

2. Cuerpos Geométricos
Los cuerpos geométricos están limitados por superficies planas
(Poliedros) o curvas (Redondos) y, a diferencia de las figuras
geométricas, poseen volumen.
Redondos Poliedros

3. Poliedros
Un poliedro es un cuerpo geométrico que está limitado por
cuatro o más polígonos.

4. Poliedros
Los poliedros pueden ser convexos y cóncavos.
Un cuerpo geométrico se dice convexo si, dados dos puntos
cualesquiera que pertenezcan a él , el segmento que los une, está
completamente contenido en el cuerpo

5. Poliedros
Poliedros cóncavos

6. Elementos de los poliedros
Caras: Polígonos que limitan el poliedro. Las caras que tienen lados
comunes con las bases son las caras laterales. La cara en la que se
apoya el poliedro y su opuesta se llaman bases.
Aristas: lados de las caras.
Aristas
Caras basales Caras laterales

7. Vértices : puntos comunes de las aristas.
Vértices

8. Fórmula de Euler
En un poliedro convexo cualquiera se cumple la siguiente relación:
C + V = A + 2
n° de caras + n° de vértices = n° de aristas + 2
C=6
V=8
A =12

9. Diagonal: segmento que une dos vértices no consecutivos del poliedro.
Puede trazarse en una misma cara o entre distintas caras.
Apotema: altura de las caras laterales.
Apotema lateral
Apotema basal
Diagonales

10. Los poliedros pueden ser regulares o irregulares

11. Video
Poliedros Regulares
Están delimitados por polígonos regulares congruentes. También son
conocidos como sólidos platónicos. (Estos son 5)
Octaedro Icosaedro
Tetraedro
Hexaedro o Cubo
Dodecaedro

12. Poliedros Regulares
Únicamente existen cinco poliedros regulares convexos, puesto que
las sumas de las caras de un ángulo poliedro tiene que ser
forzosamente menor que 360º.
No puede constituirse ningún poliedro regular con más de cinco
caras concurrentes en un mismo vértice, puesto que si tuviera seis
caras tendríamos que 6 x 60º = 360º.

13. Poliedros Regulares
Tetraedro

14. Poliedros Regulares
Octaedro

15. Poliedros Regulares
Dodecaedro

16. Poliedros Regulares
Icosaedro

17. Poliedros Regulares
Hexaedro

18. Cubo o Hexaedro regular
a V= a3
AT = 6a2
d =a 3

19. Poliedros Irregulares
Se encuentran entre ellos las prismas y las pirámides

20. Prismas
Son cuerpos geométricos que tienen dos caras paralelas y
congruentes llamadas caras basales y tres o más caras laterales
que son paralelogramos.
Arista basal
Arista lateral
Altura
Apotema basal

21. Prismas
Clasificación
Prismas
Oblicuos
Rectos
Regulares Irregulares

22. Prismas
Para nombrar un prisma se utilizan los polígonos que forman sus bases
Prisma Triangular
Prisma Pentagonal

23. Prismas
Prisma Hexagonal
Prisma Cuadrangular

24. Prismas
At = 2ABase + ALateral V = ABase ⋅ h
c
Paralelepipedo
b
a
At = 2ab + 2bc + 2ac V = a ⋅b ⋅c
d = a2 + b2 +c2

25. Pirámides
Son poliedros que tienen como base un polígono cualquiera y sus otras
caras son triángulos que concurren en un vértice común. Para nombrar
una pirámide se utiliza el polígono de su base.
Arista lateral
Apotema lateral o altura
de la cara
a Altura de la pirámide
Apotema basal
a´
Base

26. Pirámides
• Tiene una cara por base.
• Caras laterales son triángulos.
Pirámides
Oblicuas
Rectas
Regulares Irregulares

27. Pirámides
Pirámide Pentagonal Pirámide Cuadrangular
Pirámide Hexagonal Pirámide Triangular

28. Pirámides
P ( p + po )
Área= P: Perímetro
2
p:Apotema lateral
p0: Apotema basal
Abase ⋅ h
Volumen =
3

29. Cuerpos redondos
Se obtienen al girar una figura plana alrededor de un eje
• Cilindro
• Cono
• Esfera

30. Un cilindro es el cuerpo de revolución que resulta al girar un rectángulo
alrededor de un eje.

31. Cilindro
Bases: dos círculos iguales y paralelos.
Radio: el radio de las bases.
Generatriz: el lado del rectángulo opuesto al eje que genera la superficie
cilíndrica.
Eje: el lado fijo del rectángulo que, al girar sobre sí mismo, engendra al
cilindro.
Altura: la longitud de la generatriz (distancia entre las dos bases).
Superficie lateral: la cara lateral no plana, cuyo desarrollo es un
rectángulo.

32. Cilindro
Al desarrollar un cilindro se obtiene un rectángulo y dos círculos
iguales, que constituyen las bases:
• La base del rectángulo es la longitud de la circunferencia de la base.
• La altura del rectángulo es la generatriz del cilindro.

33. Área de un cilindro
A partir del desarrollo del cilindro podemos calcular su área.
Área lateral, AL: Es el área de un rectángulo cuya base es la longitud
de la circunferencia de base 2πr, y la altura, h, es la altura del
cilindro o generatriz, g:
AL = 2 · π · r · h
Área de las bases, AB: Es la suma de las áreas de las dos bases.
Como las bases son círculos, cada una tendrá un área: AB = π · r2
El área total de un cilindro es la suma del área lateral más el área de
las dos bases.
AT = AL + 2 · AB = 2πrh + 2πr2

34. Volumen de un cilindro
Si el radio del cilindro es r y la altura h, su volumen será:
Vcilindro = AB · h = π r2h

35. Un cono es un cuerpo de revolución que se genera al girar un triángulo
rectángulo alrededor de un cateto.

36. Base: el círculo sobre el que se apoya el cono.
Radio: el radio de la base.
Generatriz: el segmento que une el vértice con un punto cualquiera
de la circunferencia (coincide con la hipotenusa del triángulo
rectángulo que genera el cono).
Eje: el cateto del triángulo que, al girar sobre sí mismo, engendra
el cono.
Altura: la distancia desde el vértice a la base.
Superficie lateral: la cara lateral no plana, cuyo desarrollo es un
sector circular.

37. Área de un cono
A partir de su desarrollo podemos calcular el área de un cono.
Área lateral, AL: Es el área de un sector circular, siendo la longitud
del arco la longitud de la circunferencia de la base:
AL = Asector circular = Larco·radio del sector = 2 π r · g = π r g
2 2
Área de la base, AB:
Es el área del círculo: AB = π · r2
El área total de un cono es la suma del área lateral más el área de
la base:
AT = AL + AB = πrg + πr2

38. Volumen de un cono
El volumen del cono será igual, por tanto, a un tercio del área de la base
por la altura, es decir:
1 πr 2h
Vcono = Abase ⋅ h =
3 3

39. Esfera
La esfera es un cuerpo de revolución. Es generado por el giro de una
semicircunferencia en torno a su diámetro. No tiene desarrollo plano.
Generatriz
Centro
Eje giro
Diámetro
Radio
Eje de giro

40. Superficie de la esfera
AESFERA = 4πr2

41. Volumen de la Esfera
Consideramos la esfera dividida en multitud de pequeñas pirámides iguales con
vértice común en el centro de la esfera. La base de cada una de las pirámides es muy
pequeña, por lo que podemos considerarla plana y aplicar la fórmula del volumen de
una pirámide. Así, si llamamos AB al área de la base de la pirámide, su volumen es:
V PIRÁMIDE = AB · h = AB · r
3 3
El volumen V, de la esfera es la suma de los volúmenes de todas las pirámides:
V ESFERA = AB · r + AB · r + AB · r + ... = ( AB + AB + AB + ... ) r
3 3 3 3
La suma de las bases de todas esas pirámides será el área total de la esfera (que,
como ya sabemos, es 4πr2):
V ESFERA = ( 4 π r 2 ) · r = 4 π r 3
3 3