Este documento presenta una introducción al uso del software Maple para aplicaciones en ingeniería. Se describen conceptos matemáticos como matrices, vectores, álgebra lineal, cálculo, gráficas y ecuaciones diferenciales. También incluye ejemplos de cómo representar y manipular estos conceptos en Maple mediante comandos como matrix, evalf y plot. Finalmente, menciona algunas aplicaciones de Maple en campos como ingeniería química, civil y mecatrónica.

1. APLICACIONES A LA INGENIERÍA
CON SOFTWARE MAPLE
30 Horas
Ing. Rodolfo Alcántara Rosales
Febrero, 2016
TECNOLÓGICO DE ESTUDIOS SUPERIORES DE JILOTEPEC
DIRECCIÓN ACADÉMICA
ACADEMIA DE CIENCIAS BÁSICAS

2. I. Introducción
II. Matrices y Álgebra lineal IV. Gráficas
1. Matrices
2. Operaciones básicas con
matrices
3. Vectores
4. Productos escalar y vectorial
5. Funciones de matrices y
vectores
6. Sistema de ecuaciones
simultáneas
7. Vectores propios y de Jordan
4.1 Gráfica en dos dimensiones
4.2 Opciones de gráfica
4.3 Gráfica de puntos
4.4 Gráfica de histograma
III. Cálculo V. Aplicaciones
3.1 Límites
3.2 Límites de sucesiones
3.3 Continuidad
3.4 Derivadas
3.5 Integración
3.6 Series
3.7 Solución de ecuaciones
diferenciales
5.1 En ingeniería química
5.2 En Ingeniería en Sistemas
Computacionales
5.3 En Ingeniería Civil
5:4 En Ingeniería Mecatrónica
5.5 En Física
5.6 En Contaduría y Finanzas

3. Introducción
Maple es un programa desarrollado en 1980
por un grupo de Cálculo Simbólico de la
Universidad de Waterloo.
Al abrir el software se inicia el carácter
simbólico “>” que da inicio a un bloque de
código.
Se permite programar en maple con
sentencias conocidas en cursos de
programación.

4. Escritura
En Maple todas las
sentencias terminan con ;
(punto y coma)
También se puede utilizar :
(dos puntos) como
terminación de la línea, en
este caso no obtendríamos
ninguna salida en la
pantalla
Para escribir texto en la
ejecución lo pondremos
dentro de comillas dobles y
finalizado con punto y
coma.
Los comentarios se
preceden y terminan con #
>gausselim(A);
>B:=vector(2,[2,3]):
>"Texto en maple";
>#Comentario en Maple#

5. Variables
Las variables son
Case Sensitive, es
decir, maple distingue
mayúsculas y
minúsculas. Se utiliza
el operador de
asignación :=
En el ejemplo la
variable A se
inicializa con el valor
5.
>A:=5;

6. Operadores Matemáticos
Suma: para sumar A
y B utilizamos el
símbolo +.
Resta: para restar A y
B utilizamos el
símbolo -.
Multiplicación: para
multiplicar A y B
utilizamos el símbolo
*.
División: para dividir
A en B utilizamos /.
Potencia: A elevado a
B utilizamos ^.
>A+B;
>A-B;
>A*B;
>A/B;
>A^B;

7. Operadores Matemáticos
Modulo: el resto
entero de la división
de A en B se utiliza el
símbolo mod.
Factorial: el factorial
de A utilizamos el
símbolo !.
>A mod B;
>A!.

8. Funciones Matemáticas
Función Comando
Seno >sin(<valor>);
Coseno >cos(<valor>);
Pi >Pi;
Tangente >tan(<valor>);

9. Evalf
Un dato importante es que la escritura del siguiente comando:
>evalf(sin(5.35Pi/2));
• No arrojará el valor deseado, para proceder a la evaluación
numérica debemos encapsularlo en el comando evalf, como
sigue:
>sin(5.35Pi/2);

10. Precisión del Cálculo
Maple trabaja con una precisión de 10 decimales, si se
requiere de aumentar o disminuir la precisión se define la
variable Decimals con el valor de precisión deseado.
>Decimals:=15;
• Esto aumentará la precisión del cálculo hasta 15 decimales
durante el proyecto.

11. II. Matrices y Álgebra Lineal.

12. 2.1 Matrices.
Una matriz es un arreglo de objetos o
números. Las matrices encuentran uso y
aplicación como son los coeficientes de un
sistema de ecuaciones simultáneas o
representar las intensidades y colores de
los pixeles de una imagen.

13. Para asignar matrices en maple, se
utiliza la instrucción Matrix de la
siguiente manera:

14. EJERCICIO 1.

15. VECTORES
Un vector es una matriz con un solo
renglón, o una sola columna. Los vectores
siguen las mismas reglas que las
matrices.
a= 10i + 20j – 30k b= -15i -13j + 1.3k

16. REPRESENTACION DE
VECTORES EN MAPLE
>
>

17. OPERACIONES CON VECTORES
Para efectuar las operaciones de suma y
resta, se requieren dos vectores
respectivos para acumular el resultado,
por lo que a continuación se genera cada
uno de ellos:

18. OPERACIÓN SUMA RESTA
VECTORIAL

19. Productos escalar y vectorial
Cuando se multiplica un escalar por un
vector, se tiene como resultado un vector
mayor o menor. Para realizarla, se declara
el vector original, posteriormente el vector
que acumulara el resultado del producto:

20. PRODUCTO EESCALAR

21. PRODUCTO ESCALAR

22. Producto punto.
Es un valor escalar que se obtiene al
multiplicar componente a componente de
cada vector y posteriormente sumar los
resultados parciales. Algebraicamente se
representa como a·b.

23. Considerando los valores de los
vectores a y b, se realiza el producto
punto entre ellos:

24. Producto Cruz.
Es un nuevo vector que es perpendicular
a los vectores originales con los que se
realiza la operación. Algebraicamente se
representa como a x b.
Para obtener el producto cruz, se puede
utilizar la instrucción CrossProduct o los
símbolos &x, contenidos en la librería
LinearAlgebra, tal como se muestra en el
siguiente ejemplo

25. Producto cruz

26. POLINOMIOS

27. Tipo y Grado
Supongamos el siguiente polinomio:
> p1 := -3*x + 7*x^2 -3*x^3 + 7*x^4;
• Con ello aplicaremos el comando type, el cual evalúa si cierta
variable corresponde a una naturaleza y el comando degree
obtiene el grado del polinomio.
>type(p1,'polynom');
degree(p1);

28. Suma y Producto
Es posible realizar operaciones de suma, resta y
multiplicación de polinomios en maple. Para ello definimos
los polinomios:
>p1 := -3*x + 7*x^2 -3*x^3 + 7*x^4;
p2 := 5*x^5 + 3*x^3 + x^2 -2*x + 1;
>p1+p2;
p1-p2;
p2*p1;
• Sin embargo maple no entrega los resultados ordenados para
ello utilizamos sort.
>sort(p1+p2);
sort(p1-p2);
sort(p2*p1);

29. División
Es posible realizar la operación de división para obtener el
cuociente utilizamos la función quo y el resto rem.
>p1 := -3*x + 7*x^2 -3*x^3 + 7*x^4;
p2 := 5*x^5 + 3*x^3 + x^2 -2*x + 1;
>quo(p1,p2,x);
rem(p1,p2,x);
• Sin embargo maple no entrega los resultados ordenados para
ello utilizamos sort.
>sort(p1+p2);
sort(p1-p2);
sort(p2*p1);

30. Factorización
En maple es posible factorizar polinomios supongamos el
siguiente polinomio P.
>p:=x^2-4;
• Para factorizarlo utilizamos el comando factor :
>factor(p);

31. Máximo Común Divisor
En maple es posible obtener el máximo común divisor de dos
polinomios con el comando gcd.
>gcd(p1,p2);
>p1 := -3*x + 7*x^2 -3*x^3 + 7*x^4;
p2 := 5*x^5 + 3*x^3 + x^2 -2*x + 1;

32. Simplificación
Supongamos que tenemos la siguiente expresión racional f:
>normal(f);
> f := (x^2 + 3*x + 2)/ (x^2 + 5*x + 6);
• Para simplificarlo debemos aplicar la función normal a f.

33. Gráfica de un polinomio
En maple podemos graficar nuestro polinomio utilizando el
comando plot.
>plot(p1);
>p1 := -3*x + 7*x^2 -3*x^3 + 7*x^4;

34. POLINOMIOS DE VARIAS
VARIABLES

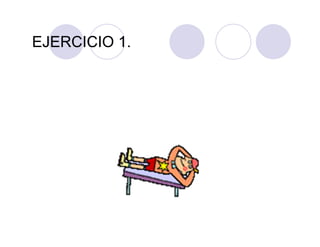
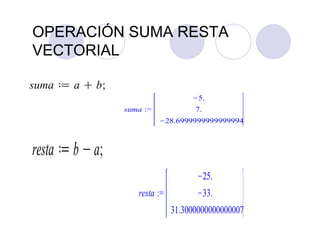
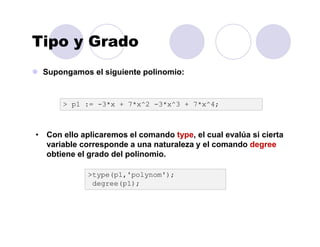
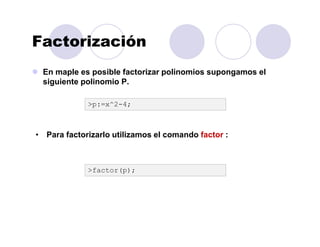
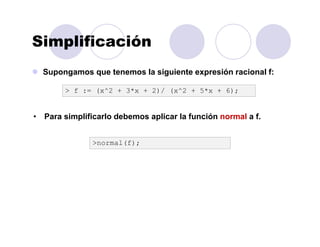
35. Ordenamiento
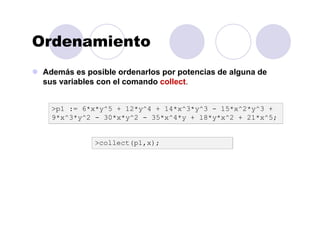
Para ordenar un polinomio de varias variables utilizaremos el
comando sort con algunos argumentos adicionales.
>p1 := 6*x*y^5 + 12*y^4 + 14*x^3*y^3 - 15*x^2*y^3 +
9*x^3*y^2 - 30*x*y^2 - 35*x^4*y + 18*y*x^2 + 21*x^5;
>sort(p1,[x,y],'plex');
• Con ello se ordenan el orden alfabético, sin embargo podemos
utilizar sort sin argumentos adicionales para ordenarlos por
potencia.
>sort(p1);

36. Ordenamiento
Además es posible ordenarlos por potencias de alguna de
sus variables con el comando collect.
>collect(p1,x);
>p1 := 6*x*y^5 + 12*y^4 + 14*x^3*y^3 - 15*x^2*y^3 +
9*x^3*y^2 - 30*x*y^2 - 35*x^4*y + 18*y*x^2 + 21*x^5;

37. ECUACIONES

38. Ecuaciones de una incógnita
En maple es posible resolver ecuaciones, para ello
supongamos la siguiente ecuación:
>ec:=x^2+6*x-3;
• Con ello definimos la variable ec, como nuestra ecuación,
para resolverla utilizamos el comando solve :
>solve(ec);

39. Ecuaciones de 2 o mas
incógnitas
En maple es posible despejar ecuaciones de 2 o mas
incógnitas, para ello supongamos la siguiente ecuación:
>ec:=x^2+6*x-3+5*y;
• Con ello definimos la variable ec, como nuestra ecuación,
para despejarla en funcion de la variable x utilizamos el
comando solve de la siguiente forma :
>solve(ec,{x});