El documento presenta los ejercicios resueltos en MATLAB del Capítulo II del libro Sistemas de Control para la Ingeniería de Norman Nise. Se definen funciones de transferencia y polinomios, y se obtienen sus raíces y se multiplican polinomios utilizando comandos de MATLAB. También se expanden funciones en fracciones parciales y se resuelve un ejemplo utilizando las herramientas matemáticas simbólicas de MATLAB.

1. DEPARTAMENTO DE ELÉCTRICA Y ELECTRÓNICA
CARRERA DE ING. EN ELECTRÓNICA E INSTRUMENTACIÓN
SISTEMAS DE CONTROL
Unidad I
DEBER 4
TEMA: Ejercicios de MATLAB del Capítulo II del Libro Sistemas de Control para la
Ingeniería de Norman Nise.
Hrs. de la asignatura
4 Hrs
Catedrático:
Ing. Franklin Silva
Estudiantes:
Pogo Rai
Sásig Edison
Tobar Emily
Fecha de entrega: 09 de Junio del 2015

2. Sistemas de Control Ing. Franklin Silva Página 2
UNIVERSIDAD DE LAS FUERZAS ARMADAS – ESPE EXTENSIÓN LATACUNGA
CARRERA DE ELECTRÓNICA E INSTRUMENTACIÓN
Sistemas de control
TEMA: Ejercicios de MATLAB del Capítulo II del Libro Sistemas de Control para la
Ingeniería de Norman Nise.
OBJETIVOS:
General:
Resolver los ejercicios de MATLAB del Capítulo II del Libro Sistemas de Control para la Ingeniería
de Norman Nise.
Específicos:
1. Aplicar los conocimientos obtenidos en el Capítulo II del Libro Sistemas de Control para la
Ingeniería de NormanNise en la resolución de ejercicios en MATLAB.
2. Aprender acerca de nuevos comandos a utilizarse para la resolución de dichos ejercicios.
3. Realizar un programa general para la resolución de ejercicios con función de transferencia.
RESUMEN:
El presente informe contiene ejemplos de resolución de ejercicios con función de transferencia,
obtención de las raíces de un sistema, representación de polinomios y conversión a un sistema LTI,
entre otros temas tratados en el Capítulo II del libro de Sistemas de Control para la Ingeniería de
Norman Nise utilizando distintos comandos y funciones de MATLAB.
ABSTRACT:
This report containsexamplesofsolving exercises with transferfunction,obtaining rootsofa system,
representation of polynomials and conversion to LTI system, among other topics covered in Chapter
II of the book Control Systems Engineering NormanNise using different commands and functions
MATLAB.
MARCO TEÓRICO
La utilización de laboratorios virtuales nos ayuda en la comprensión y resolución de una
innumerablecantidadde problemasque van desde sencillos ejercicios matemáticoshasta cuestiones
aplicables a la vida real; también nos son de mucha ayuda al momento de comprobar datos y tomar
una decisión respecto a una situación específica. MATLABes uno de los diversos programas que nos
permitenrealizareste tipo de simulacionesy pruebas,cuenta conuna grancantidaddeherramientas
y funciones que pueden ser utilizadas en diversas aplicaciones.

3. Sistemas de Control Ing. Franklin Silva Página 3
CONTROL SYSTEM TOOLBOX:
Es un conjunto de rutinas de MATLAB que ofrece algoritmos estándar de la
industria y aplicaciones para el análisis sistemático y el diseño de los sistemas de control
lineal. Puede especificar el sistema como una función de transferencia, espacio de estado, cero-polo-
ganancia o modelo de respuesta en frecuencia. Aplicaciones y funciones, como respuesta al escalón
y de Bode, permiten visualizar el comportamiento del sistema en el dominio de tiempo y
frecuencia. Puede ajustar los parámetros del compensador sintonizar utilizando ajuste del regulador
automático de PID, la formación de bucle Bode, método del lugar de raíces, diseño LQR / LQG, y
otras técnicas interactivas y automatizadas. Puede validar su diseño mediante la verificación de
tiempo de subida, el exceso, el tiempo de establecimiento, la ganancia y márgenes de fase, y otros
requisitos. (SD, MathWorks)
Características principales
 Modelos de función de transferencia, espacio de estado, cero-polo-ganancia y respuesta en
frecuencia de sistemas lineales
 Serie, paralelo, la retroalimentación y conexión general de diagrama de bloques de los
modelos lineales
 Paso respuesta , Diagrama de Nyquist, y otras herramientas de dominio de tiempo y dominio
de la frecuencia para el análisis de las medidas de estabilidad y rendimiento.
 Lugar de Raíces , diagramas de Bode , LQR, LQG, y otras técnicas de diseño de sistemas de
control clásico y espacio de estado
 La sintonización automática de controladores PID
 Conversión modelo de representación, modelo discretización de tiempo continuo, y de orden
inferior aproximación de los sistemas de orden superior.
 Algoritmos LAPACK y SLICOT optimizados para la precisión y el rendimiento

4. Sistemas de Control Ing. Franklin Silva Página 4
Figura N.-1
Herramientas de Matlab
PROCEDIMIENTO PRÁCTICO
Ejercicios
Los estudiantesque están usando MATLAB debe ahora correr el ch2p1 hasta el ch2p8 del
Apéndice B. Éste essu primer ejercicioMATLB. Aprenderána usar MATLAB para:
1) Representarpolinomios.
2) Hallar raíces de polinomios.
3) Multiplicarpolinomio.
4) Encontrar expansionesenfraccionesparciales.Porúltimo,el ejercicio2.3 se resolveráusando
el MATLAB.
PROGRAMA CH2P1
Se usarán las cadenasde bitspara identificarpartesde este tutorial enlasalidade sucomputadora.
Las cadenas de bits se representan mediante el texto encerrado entre apóstrofos, tales como ‘ab’.
Los comentarios se inician con el signo de % y MATLAB los ignora. Los números se ingresan sin
ningunootroscaracteres.Laaritméticase llevaacabomediante operadoresaritméticosapropiados.

5. Sistemas de Control Ing. Franklin Silva Página 5
'(ch2p1)' %Desplegar etiqueta
'Como estás?' %Mostrar cadena
-3.96 %Mostrar el escalar -3.96
-4+7i %Mostrar el número complejo -4+7i
-5-6j %Mostrar el número complejo -5-6i
(-4+7i)+(-5-6i) %Suma de dos números complejos
%y mostrar la suma.
(-4+7i)*(-5-6i) %Multiplicación de dos números complejos
%y mostrar el producto
M=5 %Asigna 5 a M y mostrar.
N=6 %Asigna 6 a N y mostrar.
P=M+N %Asigna M+N a P y mostrar.
Pause

6. Sistemas de Control Ing. Franklin Silva Página 6
Figura N.-2
Respuesta del corrido del programa ch2p1
PROGRAMA CH2P2
Los polinomios en s se pueden representar como vectores renglón que contienen los coeficientes.
De esta manera P1=s3
+7s2
-3s+23 se puede representar mediante el vector que se muestra a
continuaciónconoselementosseparadosmedianteunespacioocoma.Se puedenusarlacadenade
bitspara identificarcadauna de lasseccionesde este tutorial.
'(ch2p2)' %Desplegar etiqueta
P1=[1 7 -3 23] %Almacenar polinomio s^3+7s^2-3s+
%23 como P1 y mostrar.
Figura N.-3
Respuesta del corrido del programa ch2p2
PROGRAMA CH2P3
Ejecutar las declaraciones anteriores hace que MATLAB muestre los resultados. El terminar un
comandocon unpunto y coma suprime laexhibiciónde losresultados.Al escribirunaexpresiónsin
asignaciónenel primermiembroysinpuntoycomahace que laexpresiónseaevaluadaydespliegue
el resultado.

7. Sistemas de Control Ing. Franklin Silva Página 7
'(ch2p3)' %Desplegar etiqueta
P2=[3 5 7 8]; %Asigna 3s^3+5s^2+7s+8 a P2
%sin despliegue.
3*5 %Evaluar 3*5 y desplegar el resultado.
Figura N.-4
Respuesta del corrido del programa ch2p3
PROGRAMA CH2P4
Una función F(s) en forma factorizada se puede representar en forma polinomial. De este modo
P3=(s+2) (s+5) (s+6) se puede transformar en un polinomio usando el comando poly (V), done V es
un vector renglón que contiene las raíces del polinomio y poly (V) forma los coeficientes del
polinomio.
'(ch2p4)' %Desplegar etiqueta
P3=poly([-2 -5 -6]) %Asigna 3s^3+5s^2+7s+8 a P2
%sin despliegue.
3*5 %Evaluar 3*5 y desplegar el resultado
Figura N.-5
Respuesta del corrido del programa ch2p4

8. Sistemas de Control Ing. Franklin Silva Página 8
PROGRAMA CH2P5
Se puede determinar las raíces mediante el comando roots (V). Las raíces se regresan como una
vectorcolumna.Porejemplo,encuentre lasraícesde 5s4
+7s3
+9s2
-3s+2=0.
'(ch2p5)' %Desplegar etiqueta
P4=[5 7 9 -3 2] %Forma 5s^4+7s^3+9s^2-3s+2 y
despliega
rootsP4= roots(P4) %sin despliegue.
%Determinar las raices
5s^4+7s^3+9s^2-3s+2,
%Asigna a rootsP4, y despliega
pause
Figura N.-6
Respuesta del corrido del programa ch2p5
PROGRAMA CH2P6
Dos polinomios se pueden multiplicar entre si al usar el comando conv(a,b) (lo que significa
convolución).De estamanera,P5=(s3
+7s2
+10s+9)(s4
-3s3
+6s2
+2s+1) se generacomosigue:
'(ch2p6)' %Desplegar etiqueta

9. Sistemas de Control Ing. Franklin Silva Página 9
P5=conv([1 7 10 9],[1 -3 6 2 1]) %Forma (s^3+7s^2+10s+9)(s^4-
3s^3+6s^2+2s+1), asignar a P5 y despliega.
Figura N.-7
Respuesta del corrido del programa ch2p6
PROGRAMA CH2P7
La expansiónenfraccionesparcialesparaF(s)=b(s)/a(s) se puede encontrarusandoel comando [K,
p, k]= residue (b, a) (K= residuo; p= raíces del denominador, k= coeficiente directo, lo cual se
encuentra mediante la división de los polinomios antes de realizar la expansión en fracciones
parciales). Comounejemplose expandeF(s)=(7s2
+9s+12)/[s(s+7)(s2
+10s+100)].
'(ch2p7)' %Desplegar etiqueta
numf=[7 9 12]; %Definir el numerador de
P(s)
denf=conv(poly([0 -7]),[1 10 100]); %Definir el denominador de
P(s)
[K,p,k]=residue(numf, denf) %Encontrar los residuos y
asignarlos

10. Sistemas de Control Ing. Franklin Silva Página 10
Figura N.-8
Respuesta del corrido del programa ch2p6
PROGRAMA CH2P8
(Ejemplo2.3) Realicemosel ejemplo2.3del libromediante MATLAB.
'(ch2p8) Example 2.3' %Desplegar etiqueta
numy=32; %Definir el numerador
deny=poly([0 -4 -8]); %Definir el denominador
[r,p,k]=residue(numy, deny) %Calcular los residuos, polos y
%el cociente directo.

11. Sistemas de Control Ing. Franklin Silva Página 11
Figura N.-9
Respuesta del corrido del programa ch2p8
Los estudiantes que trabajen los ejercicios en MATLAB, y deseen explorar las rutinas de matemáticas
simbólicas (Symbolic Math Toolbox del MATLAB), deben correr el ch2sp1 y el ch2sp2 del Apéndice E.
Aprenderán a construir objetos simbólicos y luego hallar las transformadas de Laplace y transformadas
inversasde Laplace de funcionesenlafrecuenciayen el tiempo,respectivamente.Los ejemplosenel Caso
2 y Caso 3 de esta sección se resolverán usando las rutinas de matemáticas simbólica Symbolic Math
Toolbox
PROGRAMA CH2SP1
Modeladoenel dominiode lafrecuencia
ch2sp1 El poder de cálculo de MATLAB se ve enriquecido ampliamente al usar las Rutinasde Matemáticas
Simbólicas.Eneste ejemplose demuestrasupodermedianteel cálculode transformadasinversasde F(s).El
inicio de cualquier cálculo simbólico requiere definir los objetos simbólicos. Por ejemplo, la variable de
transformadade Laplace,s,olavariablede tiempo,t,se debendefinircomoobjetossimbólicos.Ladefinición
se realiza mediante el uso del comando syms. De esta manera syms s define s como un objeto simbólico;
symst define tcomo unobjetosimbólico:symsst define as y t ambas comoobjetossimbólicos.Solamente
se necesitan definir los objetos que entran al programa. Las variables producidas por el programa no
necesitandefinirse.De este modo,si se estádeterminandotransformadasinversasde Laplace,solamente se
necesitadefinirscomoobjetosimbólico,puestoque tresultadelcálculo.Unavezque se defineel objeto,se
puede escribirFcomouna funciónde scomo se hace normalmente amano.

12. Sistemas de Control Ing. Franklin Silva Página 12
No se tienen que usar vectores para representar el numerador y el denominador. Las transformadas de
Laplace de funciones del tiempo también se pueden imprimir en MATLAB Command Window como
normalmente se escriben.Estaforma se denominaimpresiónbonita.El comandoes pretty(F), donde F es
lafunciónque se quiere imprimirenbonito.El siguientecódigo,ustedpuedeverladiferenciaentre impresión
normal e impresiónbonitasi ustedcorre el códigosinlospuntosy coma en lospasosdonde lasfunciones,F
o f, se definen.Una vezque F se define comoF(s),se puede determinarlatransformadainversade Laplace
al usar el comando Laplace (F).En el siguienteejemplose determinanlastransformadasinversasde Laplace
de las funcionesde frecuenciaenlosejemplosusadosparaloscasos2 y 3 enla sección2.2 del libro
Caso 2:
𝐹( 𝑠) =
2
( 𝑠 + 1)( 𝑠 + 2)2 =
𝐾1
𝑠 + 1
+
𝐾2
( 𝑠 + 2)2 +
𝐾3
𝑠 + 2
𝐹( 𝑠) =
2
( 𝑠 + 1)( 𝑠 + 2)2 =
2
𝑠 + 1
−
2
( 𝑠 + 2)2 −
2
𝑠 + 2
𝑓( 𝑡) = (2𝑒−𝑡 − 2𝑒−2𝑡 − 2𝑡𝑒−2𝑡) 𝑢( 𝑡)
Caso 3:
𝐹( 𝑠) =
3
𝑠( 𝑠2 + 2𝑠 + 5)
=
𝐾1
𝑠
+
𝐾2 𝑠 + 𝐾3
𝑠2 + 2𝑠 + 5
𝐹( 𝑠) =
3
𝑠( 𝑠2 + 2𝑠 + 5)
=
3
5
(
1
𝑠
) −
3
5
( 𝑠 + 2)
𝑠2 + 2𝑠 + 5
𝑓( 𝑡) = [
3
5
−
3
5
𝑒−𝑡 (cos(2𝑡) +
1
2
𝑠𝑒𝑛(2𝑡))] 𝑢(𝑡)
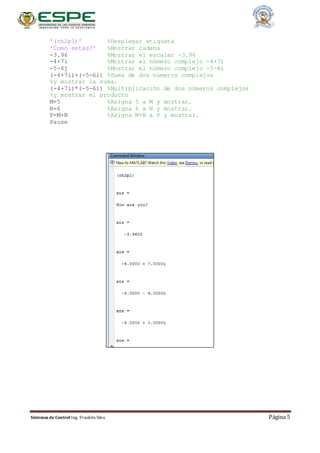
'(chsp1)'; % Desplegar etiqueta
syms s %Construir el objeto simbolico para la variable de laplace s
'Transfomada inversa de Laplace';
F=2/[(s+1)*(s+2)^2]; % Definir F(s) para el caso 2 del ejemplo
'F(s) from Caso 2'; %Desplegar etiqueta
pretty (F) %Impresion en bonio de F(s)
f=ilaplace(F); %Determinar la trasfomada inversa de Laplace
'f(t) for Caso 2'; %Desplegar etiqueta
pretty (f) %Impresion en bonito de f(t) para el caso 2
F=3/[s*(s^2+2*s+5)]; %Definir F(s) para el caso 3 ejemplo.
'f(t) for Caso 3'; %Desplegar etiqueta
pretty (f) % Impresion en bonito de f(t) para el caso 3
pause

13. Sistemas de Control Ing. Franklin Silva Página 13
Figura N.-10
Respuesta del corrido del programa ch2sp1
PROGRAMA CH2SP2
ch2sp2 En este ejemplose determinalatransformadade Laplace defuncionesdel tiempousandoelcomando
laplace(f), donde f es una función del tiempo, f(t). Como un ejemplo se usan las funciones del tiempo que
resultan de los casos 2 y 3 en la sección 2.2 en el texto y trabajamos en inverso para obtener sus
transformadasde Laplace.Veremosque el comandoLaplace(f) daF(s) enfraccionesparciales.Ademásde la
impresión bonita estudiada en el ejemplo anterior, las Rutinas de Matemáticas Simbólica contienen otros
comandosque cambian la aparienciade losresultadosdesplegadosparalegibilidadyforma.Algunosde los
comandos son collect(F), reúne los términos con coeficientes comunes de F; expand (F)-expande los
productosde factores; factor(F) –factoresde F;simple(F)- determinalaformamássencillade Fconel menor
númerode términos;simplify(F) –simplificaF;vpa (expresssion,palces) –quiere decirprecisiónaritmética
variable;este comandoconvierte términossimbólicosfraccionariosentérminosdecimales conun número
específico de decimales. Por ejemplo, la fracción simbólica 3/16 se convertirá en 0.1875 si el argumento
placesfuera4. En el siguienteejemplose determinalatrasformadade Laplace de unafuncióndel tiempo.El
resultadose despliegacomofraccionesparciales.Paracombinarlas fraccionesparcialesse usa el comando
simplify(F), donde F es la transformada de Laplace de f(t) determinada a partir de laplace(f). Por último se
usa F=vpa(F,3) paraconvertirlasfraccionessimbólicasadecimal enel resultadodesplegado
'(ch2sp2)'; %Desplegar etiqueta
syms t %Construir objeto simbolico para la variable de tiempo
'Transformada de Laplace';
'f(t) from Case 2' ; %Desplegar etiqueta
f=2*exp(-t)-2*t*exp(-2*t)-2*exp(-2*t); %Definir f(t) para el Caso 2 del ejemplo
pretty(f) %Imprimir en bonito f(t) para Caso 2 del ejemplo
'F(s) for Case 2' ; %Desplegar etiqueta
F=laplace (f);
pretty (F) %Imprimir en bonito las fracciones parciales de F(s) para
Cso 2
F=simplify(F) %Combinar las fracciones parciales
pretty(F) %Imprimir en bonito las fracciones parciales combinadas
'f(t) for Caso 3' ; %Desplegar etiqueta

14. Sistemas de Control Ing. Franklin Silva Página 14
f=3/5-3/5*exp(-t)*[cos(2*t)+(1/2)*sin(2*t)]; % Dwefinir f(t)
pretty(f) %Imprimir en bonito f(t)
'F(s) para el caso 3-Fracciones simbolicas' ;%Desplegar etiqueta
F=laplace(f); %Determinar la transformada de Laplace
pretty(F) %Imprimir en bonito las fraccion parciales
'F(s) para el caso 3 - Representacion decimal';
F=vpa(F,3); %Convertir fracciones numericas simbolicas a presentacion
decimal de 3 cifras para F(s)
pretty(F) %Imprimir en bonito las fracciones pariales combinadas
pause
Figura N.-11
Respuesta del corrido del programa ch2sp2_caso 2

15. Sistemas de Control Ing. Franklin Silva Página 15
Figura N.-12
Respuesta del corrido del programa ch2sp2_caso3
Los estudiantes que están usando Matlab deben correr ahora el ch2p9 al ch2p11 del apéndice B.
Aprenderán a usar Matlab para crear funciones de transferencia con numeradores y denominadores en
polinomiosoen forma factorizada. Tambiénaprenderán a convertir lospolinomios y su forma factorizada
CH2P9 CREACIÓN DE FUNCIONESDE TRANSFERENCIA
Método vectorial, forma polinomial: Una función de transferencia se puede expresar como un polinomio
del numeradorentre el polinomiodel denominadoresdecirF(s)=N(s)/D(s).El numerador N(s),se representa
mediante unvectorrenglón,numf,que contiene loscoeficientesde N(s).De manerasimilarel denominador
D(s),se representamediante unrenglóndenf,que contiene loscoeficientesde D(s).
Método vectorial, forma factorizada: También se pueden crear funciones de transferencia LTI si el
numerador y el denominador están expresados en forma factorizada. Esto se logra mediante el uso de
vectoresrenglónquecontienenlasraícesdel numeradorydel denominador.De estemodoG(s)=K*N(s)/D(s)
expresadocomoG=zpk(numg,deng,K).
Método de la expresión racional en s, forma polinomial (Se requieren las Rutinas de Sistemas de Control
4.2): Este método permite escribir la función de transferencia como usted lo hace normalmente. La
declaracións=tf(‘s’) debeprecederalafunciónde transferenciasi se deseacrearunafuncióndetransferencia
LTI en laforma polinomial equivalente aque se tiene al usarG=tf(numg,deng).
Método de la expresiónracional en s, forma factorizada (Se requierenlas Rutinas de Sistemas de Control
4.2): Este método permite escribir la función de transferencia como usted lo hace normalmente. La
declaración s=zpk(‘s’) debe preceder a la función de transferencia si se desea crear una función de
transferenciaLTIenla formapolinomial equivalenteaque se tiene al usarG=zpk(numg,deng,K).

16. Sistemas de Control Ing. Franklin Silva Página 16
PROGRAMA CH2P9
'(ch2p9)' %Desplegar etiqueta
'Método vectorial, forma polinomial' %Desplegar etiqueta
numf=150*[1 2 7] %Almacenar 150(s^2+2s+7)
denf=[1 5 4 0] %Almacenar s(s+1)(s+4)
'F(s)' %Desplegar etiqueta
F=tf(numf, denf) %Forma F(s) y despliega
clear %Limpia variables
pause
'Método vectorial, forma factorizada'%Desplegar etiqueta
numg=[-2 .4] %Almacena (s+2)(s+4)
deng=[-7 -8 -9] %Almacena (s+7)(s+8)(s+9)
K=20 %Definir K
'G(s)' %Desplegar etiqueta
G=zpk(numg,deng,K) %Forma G(s) y despliega
clear %Limpia variables
pause
'Método de la expresión racional' %Desplegar etiqueta
s=tf('s') %Definir 's'
P=150*(s^2+2*s+7)/[s*(s^2+5*s+4)] %Forma F(s) como una
%funcion de transferencia
%LTI forma polinomial
G=20*(s+2)*(s+4)/[(s+7)*(s+8)*(s+9)] %Forma G(s) como una
%funcion de transferencia
%LTI forma polinomial
clear %Limpia variables
pause
'Método de la expresión racional, forma factorizada'
%Desplegar etiqueta
s=zpk('s') %Definir 's'
P=150*(s^2+2*s+7)/[s*(s^2+5*s+4)] %Forma F(s) como una
%funcion de transferencia
%LTI forma factorizada.
G=20*(s+2)*(s+4)/[(s+7)*(s+8)*(s+9)] %Forma G(s) como una
%funcion de transferencia
%LTI forma factorizada.
pause

17. Sistemas de Control Ing. Franklin Silva Página 17
Figura N.-13
Respuesta del corrido del programa ch2p9

18. Sistemas de Control Ing. Franklin Silva Página 18
Figura N.-14
Respuesta del corrido del programa ch2p9
Figura N.-15
Respuesta del corrido del programa ch2p9

19. Sistemas de Control Ing. Franklin Silva Página 19
Figura N.-16
Respuesta del corrido del programa ch2p9
PROGRAMA CH2P10
Los vectoresdel numeradorydel denominadorde lafunciónde transferenciapuedenconvertirde laforma
polinomial que contienen coeficientes y la forma factorizada que contienen raíces. La función de MATLAB
tf2zp(numtf,dentf) convierte numeradorydenominadorde coeficientesaraíces.
'(ch2p10)' %Desplegar etiqueta
'Coefficients for F(s)' %Desplegar etiqueta
numftf=[10 40 60] %Forma numerador de F(s)
denftf=[1 4 5 7] %Forma denominador de F(s)
'Roots for F(s)' %Desplegar etiqueta
[numfzp,denfzp]=tf2zp(numftf,denftf)
%Convierte F(s) a forma
%factorizada
'Roots for G(s)' %Desplegar etiqueta
numgzp=[-2 -4 ] %Forma numerador de G(s)
K=10
dengzp=[0-3 -5] %Forma denominador de G(s)
'Coefficients for G(s)' %Desplegar etiqueta
[numgtf,dengtf]=zp2tf(numgzp',dengzp',K)
%Convierte G(s) a la forma
%polinomial.

20. Sistemas de Control Ing. Franklin Silva Página 20
Figura N.-17
Respuesta del corrido del programa ch2p10
Figura N.-18
Respuesta del corrido del programa ch2p10

21. Sistemas de Control Ing. Franklin Silva Página 21
Figura N.-19
Respuesta del corrido del programa ch2p10
PROGRAMA CH2P11
Los modelosLTItambiénse puedenconvertirde laformapolinomial laformafactorizada.Loscomandosde
MATLAB tf y zpk se usan para la conversión entre modelos LTI. Si una función de transferencia Fzpk(s) se
expresa como factores en el numerador y el denominador, entonces tf(Fxzpk) convierte a Fzpk(s) a una
funciónde trasferenciaexpresadacomocoeficientesenelnumeradoryenel denominador.De modosimilar,
si la funciónde transferenciaFtf(s) se expresacomocoeficientesennumeradoyendenominador.
'(ch2p11)' %Desplegar etiqueta
'Fzpk(s)' %Desplegar etiqueta
Fzpk1=zpk([-2 -4],[0 -3 -5],10) %Forma Fzpk1(s)
'Ftf1' %Desplegar etiqueta
Ftf1=tf(Fzpk1) %Convierte Fzpk1(s) a
%forma de coeficientes
'Ftf2' %Desplegar etiqueta
Ftf2=tf([10 40 60],[1 4 5 7]) %Forma Ftf2(s)
'Fzpk2' %Desplegar etiqueta
Fzpk2=zpk(Ftf2) %Convierte Ftf2(s) a
%forma factorizada.

22. Sistemas de Control Ing. Franklin Silva Página 22
Figura N.-20
Respuesta del corrido del programa ch2p11
Figura N.-21
Respuesta del corrido del programa ch2p11

23. Sistemas de Control Ing. Franklin Silva Página 23
Los estudiantesque trabajan los ejerciciosde Matlab y deseenexplorarlas rutinas, debencorrer ahora el
ch2sp3 del apéndice E .Aprenderán a usar las rutinas de matemática simbólicapara simplificarla entrada
de funciones de transferencia complicadas, así como mejorar su legibilidad. Aprenderá a introducir una
función de transferencia simbólicay convertirla enun objetolineal en invariante en el tiempo (LTI) como
se presentaenel apéndice B, ch2p9.
PROGRAMA CH2SP3
SymbolicMathToolbox deMATLABse puedeutilizarparasimplificarlaentradade funcionesdetransferencia
complicadocomo sigue:Inicialmente,laentradade lafunciónde transferencia,G(s) =numg/ Deng, através
de declaraciones de matemáticas simbólicas. Entonces, convertir G (s) a una función de transferencia de
objetos LTI. Estaconversiónse realizaendos pasos. El primerpaso utilizaelcomando [numg, deng]=numden
(G) para extraerel numeradoryel denominadorsimbólicode G.El segundopaso convierte,porseparado, el
numerador y el denominador de vectores mediante el sym2poly (S) del sistema, donde S es un polinomio
simbólico. El últimopaso consiste enlaformación de la función de transferenciade objetos LTI utilizandola
representaciónvectorial de numeradoryel denominadorde lafunciónde transferencia.
A modode ejemplo,formamos el objetoLTI,G (s) = [54 (s+ 27) (S^ 3 + 52s ^ 2 + 37s + 73)] / [s(s ^ 4 + 872s
^ 3 + 437s ^ 2 + 89s + 65) (s ^ 2 + 79s + 36)] haciendo uso de Symbolic Math Toolbox de MATLAB para la
simplicidady legibilidad
'(ch2sp3)' % visualizacion de etiqueta
syms s % construya objeto simbolico para
% variable de frecuencia's'.
G=54*(s+27)*(s^3+52*s^2+37*s+73)...
/(s*(s^4+872*s^3+437*s^2+89*s+65)*(s^2+79*s+36));
% formar simbolo G(s).
'Symbolic G(s)' % visualizacion de etiqueta.
pretty(G) % impresion del simbolo G(s).
[numg,deng]=numden(G); % extraer simbolo del numerador y denominador.
numg=sym2poly(numg); % Formar vector para numerador de G(s).
deng=sym2poly(deng); % Formar vector para denominador de G(s).
'LTI G(s) in Polynomial Form' % visualizacion de etiqueta.
Gtf=tf(numg,deng) % Formar y mostrar objetos para G(s) en
% forma polinomica.
'LTI G(s) in Factored Form' % visualizacion de etiqueta.
Gzpk=zpk(Gtf) % Convertir G(s) en forma factorizada.

24. Sistemas de Control Ing. Franklin Silva Página 24
Figura N.-22
Respuesta del corrido del programa ch2sp3
PROGRAMA CH2P9
'(ch2p9)' %Desplegar etiqueta
'Método vectorial, forma polinomial' %Desplegar etiqueta
numf=150*[1 2 7] %Almacenar 150(s^2+2s+7)
denf=[1 5 4 0] %Almacenar s(s+1)(s+4)
'F(s)' %Desplegar etiqueta
F=tf(numf, denf) %Forma F(s) y despliega
clear %Limpia variables
pause

25. Sistemas de Control Ing. Franklin Silva Página 25
Figura N.-23
Respuesta del corrido del programa ch2sp9
'Método vectorial, forma factorizada'%Desplegar etiqueta
numg=[-2 .4] %Almacena (s+2)(s+4)
deng=[-7 -8 -9] %Almacena (s+7)(s+8)(s+9)
K=20 %Definir K
'G(s)' %Desplegar etiqueta
G=zpk(numg,deng,K) %Forma G(s) y despliega
clear %Limpia variables
pause

26. Sistemas de Control Ing. Franklin Silva Página 26
Figura N.-24
Respuesta del corrido del programa ch2sp9
'Método de la expresión racional' %Desplegar etiqueta
s=tf('s') %Definir 's'
P=150*(s^2+2*s+7)/[s*(s^2+5*s+4)] %Forma F(s) como una
%funcion de transferencia
%LTI forma polinomial
G=20*(s+2)*(s+4)/[(s+7)*(s+8)*(s+9)] %Forma G(s) como una
%funcion de transferencia
%LTI forma polinomial
clear %Limpia variables
pause

27. Sistemas de Control Ing. Franklin Silva Página 27
Figura N.-25
Respuesta del corrido del programa ch2sp9
'Método de la expresión racional, forma factorizada'
%Desplegar etiqueta
s=zpk('s') %Definir 's'
P=150*(s^2+2*s+7)/[s*(s^2+5*s+4)] %Forma F(s) como una
%funcion de transferencia
%LTI forma factorizada.
G=20*(s+2)*(s+4)/[(s+7)*(s+8)*(s+9)] %Forma G(s) como una
%funcion de transferencia
%LTI forma factorizada.
Pause
Figura N.-26
Respuesta del corrido del programa ch2sp9
Los estudiantes que estén trabajando ejercicios de MATLAB, y deseen explorar la capacidad agregada de
las rutinasde matemática simbólicadel MATLAB, debenahoracorrer el ch2sp4 del Apéndice E,donde está
resueltoel ejemplo2.10. Aprenderána usar las rutinas de matemática simbólicapara resolverecuaciones
simultaneas, usando la regla de Cramer, Específicamente, las rutinas de matemática simbólica se usaran
para despejarla funciónde transferenciade la ecuación(2.82), utilizandolasecuaciones(2.80)

28. Sistemas de Control Ing. Franklin Silva Página 28
PROGRAMA CH2SP4
ch2sp4 (Ejemplo2.10) La Rutinas de Matemáticas Simbólicas de MATLAB se pueden usar para simplificar la
solución de ecuacionessimultáneasmediante lareglade Cramer.Un sistemade ecuacionessimultaneas se
pueden representar mediante Ax=B, donde A es una matriz formada por los coeficientes de las incógnitas
en las ecuaciones simultaneas, x es el vector de incógnitas y B es un vector que contiene las entradas. La
regla de Cramer establece que xk = det(Ak)/ det(A) , donde Ak es la matriz formada al reemplazar la k-
ésima columna de la matriz A con el vector de entrada B . En el texto, se denomina det(A) como delta. En
MATLAB, las matrices se escriben con espacio o coma para separar los elementos para cada uno de los
reglones.El siguiente reglón se indicaconun puntoy coma o retornode carro.
La matrizcompletaestá encerradaentre un par de paréntesiscuadrados.Al aplicarlo anteriora la solución
del ejemplo 2.10 A=[(R1+L*s)-L*s; -L*s(L*s+R2 +(1/(C*s)))] y Ak=[(R1+L*s) V;-L*s 0]. La función det(matrix)
evalúa el determinante de una matriz cuadrada que se usa como argumento. Determinemosla función de
transferencia, G(s) = I2(s)/V(s),solicitadaenelejemplo2.10.El comandosimple(s),dondesesunafunción
simbólica,se introduce enlasolución.El comandosimple(s) simplificalasoluciónal reducirla longitudde s.
El usode simple(s) simplificalasoluciónal reducirlalongitudde s.El uso de simple (I2) reduce lasoluciónal
combinarpotenciasigualesde lavariable de Laplace,s
Ejemplo2.10
Funcione transferenciay lazos múltiples
Problema
Dada la redde lafigura2.6a, encuentre lafunciónde transferencia 𝐼2(𝑠)/𝑉(𝑠)
Figura N.-27
Circuito RLC
[ 𝑉( 𝑠)
0
] = [
𝐿𝑠 + 𝑅1 −𝐿𝑠
−𝐿𝑠 𝐿𝑠 + 𝑅2 +
1
𝑠𝐶
][
𝐼1
( 𝑠)
𝐼2
( 𝑠)
]
𝐼2
( 𝑠) =
| 𝐿𝑠 + 𝑅1 𝑉( 𝑠)
−𝐿𝑠 0
|
|
𝐿𝑠 + 𝑅1 −𝐿𝑠
−𝐿𝑠 𝐿𝑠 + 𝑅2 +
1
𝑠𝐶
|
=
𝐿𝑠𝑉( 𝑠)
𝐿2 𝑠2 + 𝑅2 𝐿𝑠 +
𝐿
𝐶
+ 𝑅1 𝐿𝑠 + 𝑅1 𝑅2 +
𝑅1
𝑠𝐶
− 𝐿2 𝑠2
𝐼2
( 𝑠)
𝑉( 𝑠)
=
𝐿𝐶𝑠2
( 𝑅1 + 𝑅2
) 𝐿𝑠2 𝐶 + ( 𝑅1 𝑅2 𝐶 + 𝐿) 𝑠 + 𝑅1

29. Sistemas de Control Ing. Franklin Silva Página 29
Figura N.-28
Respuesta del corrido del programa ch2sp4
ANLISIS DE RESULTADOS
En la resolución de ecuaciones no homogéneas que implican funciones discontinuas, las
transformadas de Laplace es la única herramienta que tenemos a nuestra disposición y MATLAB
ayuda a resolver toda el álgebra que implica el uso de este método.
MATLAB utiliza matemática simbólica para poder reducir funciones de transferencia complicadas y
dejarlas expresadas lo cual facilita nuestro trabajo.
CONCLUSIONES

 Matlab es una herramienta que facilita el cálculo de Laplace mediante comandos
predeterminados.
 La mayor parte de problemas se deben resolver de manera simbólica antes de poder
reemplazar valores y obtener resultados, por esta razón MATLAB posee una herramienta de
matemática simbólica la cual permite resolver funciones de transferencia muy complicadas.
RECOMENDACIONES
 Se debe declarar variables fáciles de recordar para así evitar errores al momento de la
compilación del programa para su ejecución.
BIBLIOGRAFÍA
[1] Nise, N. (2006). Sistemas de control para ingeniería (Tercera Edición ed.). México: Editorial
Continental.