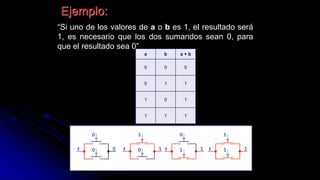
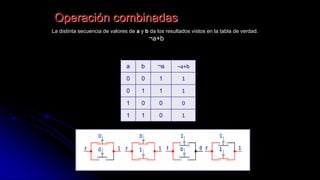
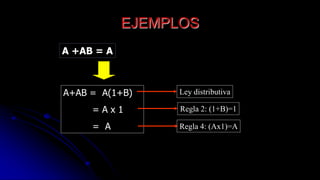
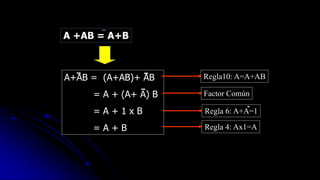
El documento describe las operaciones fundamentales del álgebra de Boole, incluyendo la suma, el producto y la negación. Define el álgebra de Boole como una estructura algebraica que formaliza las operaciones lógicas Y, O y NO. También explica que el álgebra de Boole se utiliza para modelar sistemas digitales.

1. Universidad Fermín Toro
Departamento de formación general
Facultad de Ingeniería
Aumno: Darwing leon
Profesor: Edecio Freitez
Estructuras Discretas II

2. OPERACIONES
Hemos definido el conjunto A = {0,1} como el conjunto universal sobre el
que se aplic el álgebra de Boole, sobre estos elementos se definen varias
operaciones, veamos las más fundamentales:
Operación suma
La operación suma (+) asigna a cada par de valores a, b de A un valor c
de A:
a +b=c
Su equivalencia en lógica de interruptores es un circuito de dos
interruptores en paralelo

3. ALGEBRA DE BOOLE
Es una estructura algebraica que rigorizan las operaciones lógicas
Y, O y NO, así como el conjunto de operaciones unión, intersección
y complemento.
Se denomina así en honor a George Boole, (2 de noviembre de
1815 a 8 de diciembre de 1864), matemático inglés que fue el
primero en definirla como parte de un sistema lógico a mediados
del siglo XIX. Específicamente, el álgebra de Boole fue un intento
de utilizar las técnicas algebraicas para tratar expresiones de la
lógica proposicional. En la actualidad, el álgebra de Boole se aplica
de forma generalizada en el ámbito del diseño electrónico.

4. OPERACIONES
Hemos definido el conjunto A = {0,1} como el conjunto universal sobre el
que se aplica el álgebra de Boole, sobre estos elementos se definen varias
operaciones, veamos las más fundamentales:
Operación suma
La operación suma (+) asigna a cada par de valores a, b de A un valor c
de A:
a +b=c
Su equivalencia en lógica de interruptores es un circuito de dos
interruptores en paralelo

5. Ejemplo:
“Si uno de los valores de a o b es 1, el resultado será
1, es necesario que los dos sumandos sean 0, para
que el resultado sea 0”
a b a + b
0 0 0
0 1 1
1 0 1
1 1 1

6. Operación producto
La operación producto ( *) ) asigna a cada par de valores a, b de A
un valor c de A:
a*b=c
Esta operación en lógica de interruptores es un circuito en serie de
dos interruptores:

7. •solo si los dos valores a y b son 1, el resultado será 1, si
uno solo de ellos es 0 el resultado será 0
a b a*b
0 0 0
0 1 0
1 0 0
1 1 1

8. Operación negación
La operación negación presenta el opuesto del valor de a
a ¬a
0 1
1 0

9. Operación combinadas
a b ¬a ¬a+b
0 0 1 1
0 1 1 1
1 0 0 0
1 1 0 1
La distinta secuencia de valores de a y b da los resultados vistos en la tabla de verdad.
¬a+b

10. ALGEBRA DE BOOLE
Lógica  Razonamiento humano
 Características:
1- Se han definido funciones binarias que llamaremos:
 aditiva (x+ y)
 multiplicativa (x*y)
 monaria (de un solo parámetro) por x'.
2- Se han definido dos elementos (que designaremos
por 0 y 1)
 Además, es una herramienta que permite modelar
los sistemas digitales.

11. FUNCIONES BÁSICAS
BOOLEANAS
 Igualdad
 Unión (función =O)
 Intersección (función
Y)
 Negación (función
NO)
 OR.
 AND.
 NOT.
Operaciones
básicas en un AB

12. LEYES DEL ALGEBRA DE BOOLE
 Conmutativa
A + B = B + A
A  B = B  A
 Asociativa
A + (B + C)= (A + B) + C
A  (B  C)= (A  B)  C
 Distributiva
A + (B  C) = (A + B)  (A + C)
A  (B + C) = (A  B) + (A  C)

13. Teoremas y Reglas
5/33
1) A + 0 = A
2) A + 1 = 1
3) A  0 = 0
4) A  1 = A
5) A + A = A
6) A + Ā = 1
7) A  A = A
8) A  Ā = 0
9) Ā = A
10) A +AB = A
11) A +AB = A+B
12) (A+B)(A+C)=A+BC

14. EJEMPLOS
0
1


aa
aa
aa 
0
1


aa
aa
aa 
cbacba
cbacba


0
1


aa
aa
aa 
cbacba
cbacba


0
1


aa
aa
aa 
cbacba
cbacba


0
1


aa
aa
aa 
cbacba
cbacba


0
1


aa
aa
aa 
cbacba
cbacba


0
1


aa
aa
aa 
cbacba
cbacba


0
1


aa
aa
aa 
cbacba
cbacba


0
1


aa
aa
aa 
cbacba
cbacba


0
1


aa
aa
aa 
cbacba
cbacba


0
1


aa
aa
aa 
cbacba
cbacba


0
1


aa
aa
aa 
cbacba
cbacba


0
1


aa
aa
aa 
cbacba
cbacba


0
1


aa
aa
aa 
cbacba
cbacba


0
1


aa
aa
aa 
cbacba
cbacba


0
1


aa
aa
aa 
cbacba
cbacba


0
1


aa
aa
aa 
cbacba
cbacba


A +AB = A
A+AB = A(1+B)
= A x 1
= A
Ley distributiva
Regla 2: (1+B)=1
Regla 4: (Ax1)=A

15. A +AB = A+B
A+AB = (A+AB)+ AB
= A + (A+ A) B
= A + 1 x B
= A + B
Regla10: A=A+AB
Factor Común
Regla 6: A+A=1
Regla 4: Ax1=A