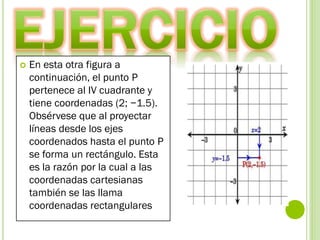
El documento explica la formación y características del plano cartesiano, incluyendo la asignación de coordenadas a puntos y la clasificación en cuadrantes. También se aborda la distancia entre puntos, ecuaciones algebraicas, y conceptos de geometría analítica como hipérbolas y secciones cónicas. Se presentan definiciones clave y ejemplos relacionados con la geometría en dos dimensiones.

2.  Se forma a partir de dos rectas
perpendiculares, cuyo punto de
intersección se llaman origen la
recta horizontal se llama eje X o eje
de la abscisa.
 Hacia la izquierda del origen los
valores son negativos y hacia la
derecha son positivos .
 La recta vertical se llama eje Y o eje
de la ordenada. Hacia abajo son
negativos y hacia arriba son positivo
 El plano cartesiano se divide en
cuatro regiones en cuadrantes a
cada punto P se le asigna una
coordenadas
 P (X, Y)

3.  En esta otra figura a
continuación, el punto P
pertenece al IV cuadrante y
tiene coordenadas (2; −1.5).
Obsérvese que al proyectar
líneas desde los ejes
coordenados hasta el punto P
se forma un rectángulo. Esta
es la razón por la cual a las
coordenadas cartesianas
también se las llama
coordenadas rectangulares

4.  La distancia entre dos
puntos equivale a la
longitud del segmento de
recta que los une,
expresado numéricamente.
Dados dos puntos
cualesquiera A(x1,y1),
B(x2,y2), definimos la
distancia entre ellos,
d(A,B), como la longitud
del segmento que los
separa.

5.  Es el punto que se
encuentra a la misma
distancia de otros dos
puntos cualquiera o
extremos de un
segmento y es el que lo
divide en dos partes
iguales

6.  Una ecuación es la igualdad existente
entre dos expresiones algebraicas
conectadas a través del signo de
igualdad en la que figuran uno o varios
valores desconocidos, llamadas
incógnitas, además de ciertos datos
conocidos. De manera, que para
representar estas generalmente se
emplean las letras, u, v, x, y, z.
 Si plantemos la ecuación algebraica,
como la mostrada a continuación,
podremos ver en ella los elementos
señalados anteriormente. Veamos:
 4x + 10 = x – 14

7.  Es un conjunto de puntos plano que equidistan de un
punto O
 Arco: segmento de circunferencias
 Radio : segmento que une el centro con un punto A
 Diámetro: segmentos que une dos
 Punto A y B de la circunferencia y
 Pasa al centro

8.  Es el lugar geométricos de todos los puntos P del plano
cuya distancia es una recta / llamada directriz y un
punto F llamado foco que no pertenece a la recta /, son
iguales.

9.  Es una curva cónica
cerrada, plana y simétrica
respecto a sus ejes mayor y
menor, perpendiculares
entre sí. Es el resultado de
la sección de un cono por
un plano oblicuo a su eje de
simetría con ángulo mayor
que el que forma la
generatriz del cono respecto
al eje de revolución.

10.  Se define como el lugar geométrico de los puntos
del plano en el que la diferencia de distancias a
dos puntos fijos denominados focos, F y F', es
siempre constante. Por ejemplo :
 Las líneas azules constituyen lo que se conoce
como una hipérbola. Observa sus focos F y F'.
Estos puntos son muy importantes ya que la
diferencia de la distancia entre cada punto P(x,y)
y estos puntos es siempre constante.
 Por tanto, debes tener en cuenta que para
cualquier punto de la hipérbola siempre se
cumple que:|d(P,F)−d(P,F')|=2⋅
 Donde d(P,F) y d(P,F') es la distancia de un punto
genérico P de la hipérbola al foco F y al foco F'
respectivamente. Y donde 2a es una constante

11.  Es el lugar geométrico de los puntos del plano (x,y)
que satisfacen una ecuación completa de segundo
grado:

12. Superficie - una superficie cónica de revolución está
engendrada por la rotación de una recta alrededor de otra
recta fija, llamada eje, a la que corta de modo oblicuo.
Generatriz - la generatriz es una cualquiera de las rectas
oblicuas.
Vértice - el vértice es el punto central donde se cortan las
generatrices.
Hojas - las hojas son las dos partes en las que el vértice
divide a la superficie cónica de revolución.
Sección - se denomina sección cónica a la curva
intersección de un cono con un plano que no pasa por su
vértice. En función de la relación existente entre el ángulo
de conicidad y la inclinación del plano respecto del eje del
cono, pueden obtenerse diferentes secciones cónicas.

14.  https://www.profesorenlinea.cl/matematica/Ecuacion
_parabola.html
 https://economipedia.com/definiciones/plano-
cartesiano.html
 https://www.superprof.es/apuntes/escolar/matemati
cas/analitica/vectores/coordenadas-del-punto-medio-
de-un-segmento.html